6R機器人柔體動力學建模及模態分析

李宇庭，李 波，閆 榮，彭芳瑜，唐小衛，陳定方

(1 武漢理工大學智能制造與控制研究所，湖北 武漢 430063；2 華中科技大學機械科學與工程學院，湖北 武漢 430074)

6R機器人柔體動力學建模及模態分析

李宇庭1，李 波1，閆 榮2，彭芳瑜2，唐小衛2，陳定方1

(1 武漢理工大學智能制造與控制研究所，湖北 武漢 430063；2 華中科技大學機械科學與工程學院，湖北 武漢 430074)

根據D-H方法建立6R機器人的連桿坐標系，在此基礎上，通過綜合考慮機器人關節柔度與臂桿柔度，利用牛頓-歐拉法得到了6R機器人的柔體動力學方程；同時，根據模態理論計算了柔性機器人固有頻率，并通過建立剛柔耦合模型進行仿真分析，驗證了理論模型的正確性。

關節柔度； 臂桿柔度； 柔體動力學； 模態理論； 剛柔耦合

由于機器人剛性較差，在機加工過程中更容易發生振動及切削不穩定現象，有必要對6R機器人進行柔體動力學建模，并進行相應的模態分析。

在機器人銑削方面，張永貴等人對加工機器人的關節柔度與結構柔度進行綜合分析，并推導出二者與機器人末端柔度的具體關系[1]，但未考慮機器人動態剛度；C. Reinl等人通過對帶有柔性關節的多剛體系統進行動力學建模，并利用相應算法對加工路徑進行離線補償以提高加工質量[2]，但其動力學方程未涉及結構柔度。在柔性關節動力學方面，潘博等人采用拉格朗日方法對空間柔性機械臂的動力學進行了建模[3]，但未分析其模態特性。本文在已有分析基礎上，建立了包含關節柔度與結構柔度的機器人動力學方程，同時對其模態特性進行了分析。

1 6R機器人模型及坐標系

利用CAD/CAM軟件對6R加工機器人進行三維建模。由于本文研究重點在于動力學建模，為簡化模型，去掉驅動電機及內部傳動部件后其虛擬樣機見圖1。從圖中可以看出，機器人結構主要由底座、大臂、小臂及手腕組成，有6個可以獨立活動的關節，分別為腰部、肩部、肘部與腕部關節。加工用電主軸在兩片半圓形裝置的夾持下安裝在末端執行器上，由各關節帶動電主軸相對工件運動，以此對工件進行銑削加工。

圖 1 6R機器人虛擬樣機

根據D-H法[4]對該機器人依次建立連桿坐標系{1}～{6}(圖2)，圖中只標出了各坐標系的x與z軸，y軸可由右手定則確定，其中坐標系{0}是機器人基座標系，坐標系方向與{1}的初始位置即θ1=0°時的方向完全重合。從圖中可以看出，該機器人共有6個連桿坐標系(不包括基座標系)，且其腕部三坐標系即{4}、{5}、{6}的原點重合。

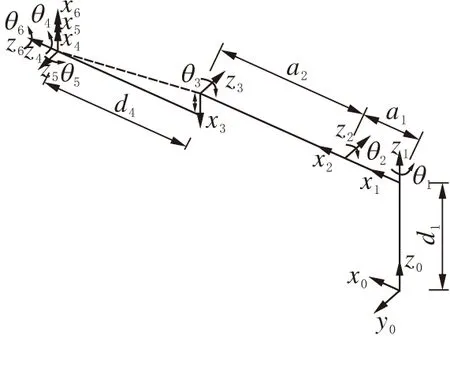
圖 2 6R機器人連桿坐標系

根據該機器人的實際技術參數，得到各連桿的4個參數及關節運動范圍(表1)。

表1 6R機器人連桿參數

2 機器人柔度模型

2.1 機器人關節柔度

為了對末端執行器進行精確控制，串聯工業機器人轉動關節需要用大剛度、高傳動精度的減速器(一般采用諧波減速器或RV減速器)來連接伺服電機與關節的運動。盡管其剛度很大，但在末端外力作用下，會導致實際輸出關節變量與規劃關節變量之間產生微小誤差，從而使末端執行器的位姿發生變化。

機器人柔性關節傳動的物理模型見圖3a，中間的機構簡圖表示傳動用RV減速器，將中間的減速器簡化為扭簧后的模型如圖3b所示，當給定伺服電機的規劃角位移q后，由于受到關節扭矩τ，連桿實際角位移為θ，得到這三者的關系如下

τ=kj·(q-θ)

(1)

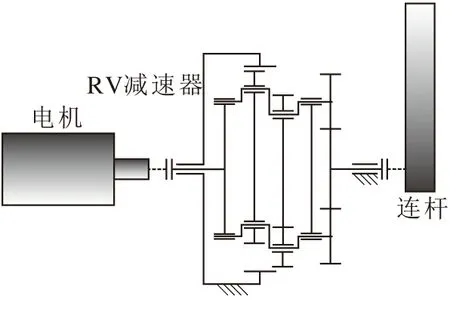
(a)機器人關節傳動物理模型

(b)機器人關節傳動簡化模型

相對于機器人前三個關節來說，機器人的腕部三關節對機器人末端振動影響較小。基于這一點，在建立含有柔性關節的機器人動力學方程時，僅考慮其前三個關節的柔性，并且將小臂與腕部視為一個整體加以建模。經過試驗測量[5]，得到該型6R機器人的前三個關節的剛度值分別為：6.88×105Nm/rad、6.88×105Nm/rad與3.78×105Nm/rad。

2.2 機器人柔性臂桿模型

由材料力學知識可知，構件在承受外力條件下一定會產生變形。對于高度耦合的機器人，其臂桿的柔性變形對末端執行器位姿的影響較大，因此在建立機器人動力學模型的過程中有必要考慮機器人臂桿的柔度。

對于任一臂桿，在末端分別加上6個方向的廣義力后，可以產生4種變形情況，即縱向拉伸、繞縱軸扭曲以及兩個方向的彎曲。根據機器人的實際構造，可以發現其繞著連桿轉軸的彎曲與關節柔性變形的方向是一致的，其對末端執行器位姿影響最大；另一方面，由機器人受力情況及截面特性(抗拉剛度及抗扭剛度較大)可知，其彎曲變形量較大，而拉伸、扭轉變形量較小。基于上述原因，本文僅考慮繞關節轉軸的彎曲變形，其受力及變形示意圖見圖4。

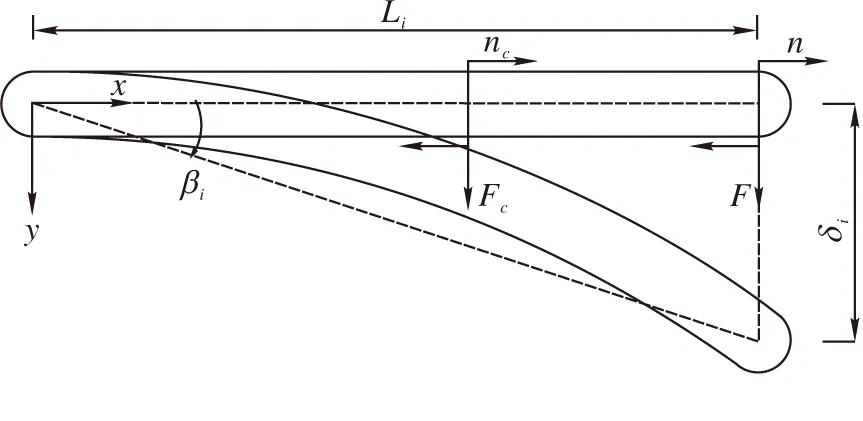
圖 4 繞關節轉軸的彎曲變形示意圖

由圖4，臂桿{i}在末端受到臂桿{i+1}繞z軸扭轉力矩n及y向作用力F，在質心受到相同方向的慣性力矩nc及慣性力Fc，上述力與力矩所產生的變形方向與關節柔度產生的變形是相同的，產生的等效關節轉角

(2)

式中，δi為連桿i末端產生的變形量；Li為連桿i長。

由機器人的構造可以明顯看出，其大臂與小臂剛度最差，對末端執行器位姿影響最大，故本文只考慮大臂與小臂的臂桿柔度。為計算臂桿各加載類型下的柔度，根據實際結構，將大臂與小臂分別簡化成空心方鋼與實心圓棒，根據材料力學相關理論可以計算出各柔度值[6](表2)。

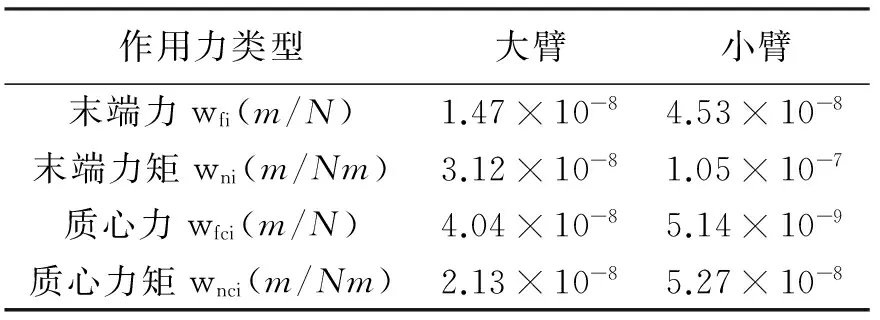
表2 各加載類型的柔度值

3 機器人柔體動力學方程

根據牛頓-歐拉法得機器人動力學[7]為

(3)

式中，M為n×n慣性力系數矩陣；C為n×n離心力系數矩陣；B為n×n科氏力系數矩陣；G為n×1重力矢量；F為n×1外部作用力矢量。

式(3)與式(1)、式(2)所述機器人柔度模型聯合起來即為機器人柔體動力學模型，其物理模型見圖5。

圖 5 機器人柔體動力學物理模型

在外力作用下，設由關節柔度引起的關節角度偏差為αi，而由臂桿柔度引起的等效關節角度偏差為βi，關節規劃角位移為qi，實際輸出角位移

θi=qi-αi-βi

(4)

所以關節輸出扭矩

τi=kjiαi=kji(qi-θi-βi)

(5)

另一方面，根據臂桿所受外力及其柔度可以求得由臂桿柔度引起的等效關節角度偏差

(6)

式中，δi、Li與式(2)完全一樣，而δfi、δni、δfci、δnci則分別表示末端受力與力矩以及質心受力與力矩所引起的臂桿末端位移量。根據柔度、力與位移的關系，臂桿末端由臂桿柔度產生的總位移量可由下面的矩陣乘積得到

δi=[wli]T·[Fli]

(7)

式中，[wli]為臂桿的柔度向量，且[wli]T=[wfiwniwfciwnci]，具體參數見表2。

[Fli]為臂桿受外力矢量，且[Fli]T=[ifi+1mini+1zifciminciz]T，m=x或y，視坐標系的方向而定。

將式(6)、(7)代入式(5)，寫成矩陣形式后再帶入到式(3)所示動力學方程中即為綜合考慮關節柔度與臂桿柔度的機器人柔體動力學方程，寫成矩陣形式為

(8)

式中，q為規劃關節變量，θ代表實際輸出關節變量，Kj表示關節剛度矩陣，即Kj=diag(kj1、kj2、kj3)，另一方面，式(8)中的系數矩陣與(3)式中的系數矩陣不一定完全相同，需要根據實際情況進行確定。

4 機器人初始位姿模態及仿真

4.1 6R機器人模態分析

為了分析得到柔性機器人的固有頻率，運用模態分析理論[8]進行機器人初始加工位姿的模態求解。設多自由度系統的運動學方程為

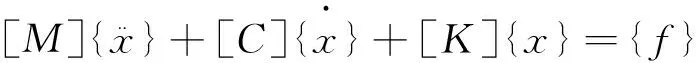
(9)

其中，[M]、[C]、[K]分別為質量矩陣、阻尼矩陣及剛度矩陣，而{x}與{f}分別表示響應向量及外力向量。對式(9)進行Laplace變換，得到

([M]s2+[C]s+[K]){X(s)}={F(s)}

(10)

為了將其轉化成一般特征值問題，式(10)被擴展為

([A]s+[B]){Y}={F'}

(11)

其中，

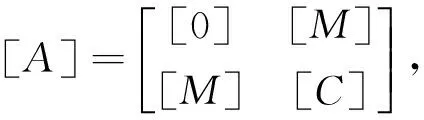
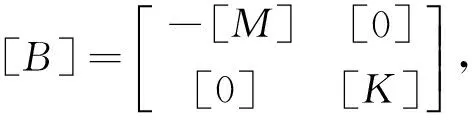
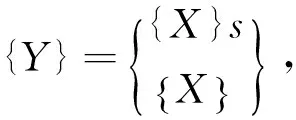
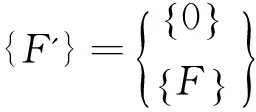
若外力向量為零，那么式(11)就成了關于實值矩陣的一般特征值問題，其特征方程為

det([A]s+[B])=0

(12)

由式(12)解得特征根s，其實部σr為阻尼因子，而虛部ωr則為阻尼固有頻率。

對于機器人加工初始位姿，且末端無切削力的條件下(即自由振動)，機器人柔體動力學方程中的速度與重力項對關節變量的實際輸出影響較小，這里忽略不計[9]，則式(9)變成

(13)

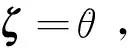
(14)

式中，初始位置質量矩陣

根據式(9)～(14)，計算得到特征值，其虛部分別為136.77rad/s、81.41rad/s及88.64rad/s，即21.77Hz、12.96Hz、14.11Hz。

4.2 模態仿真驗證

由于考慮了機器人的關節柔度及臂桿柔度，因此要建立剛柔耦合仿真模型[10]。首先在ADAMS中建立機器人的剛體模型，添加相應約束后，利用AZ()建立角位移測量函數，并在前三個關節處加上如下力矩驅動

τi=kji·(qi-θi)=kji·Δθi

(15)

然后利用柔性體替代剛性體模塊將模態中性文件導入到現有剛體模型，剛性臂桿上的原有約束及驅動自動轉移到柔體模型上，而原有marker點則轉變成與之最近的節點。建立的剛柔耦合模型見圖6，從圖6中可以發現，在運動過程中，大臂與小臂是柔性的，圖中的應力云圖說明了這一點。

圖 6 機器人剛柔耦合模型

利用ADAMS中的Vibration模塊對虛擬樣機模型進行了模態分析[11]。首先在末端刀具處建立了輸入通道，用0.1～1000Hz的諧波力進行激勵，并建立刀具x、y、z的三向輸出通道。根據輸入、輸出通道的測試信號可以得到機器人系統的模態信息。機器人振動系統共有58階模態，且為共軛關系，其固有頻率從10Hz變化到16 000Hz，這是由關節柔度及臂桿柔度所決定的，關節柔度決定低頻固有頻率，而臂桿柔度決定高頻固有頻率。圖7為刀具y向振動的模態參與因子曲線。

在圖7中，左側曲線峰值對應的頻率為11.749Hz，中間曲線峰值對應的頻率為13.804Hz，右側曲線峰值對應的頻率為21.380Hz，分別為第3、4與5階模態頻率，其他階模態參與因子與之相比很小，可以忽略不計。表3給出了第3～5階模態參數信息，包括固有頻率、阻尼比以及留數，對比理論計算結果可以看出，二者十分相近，驗證了理論分析的科學性。

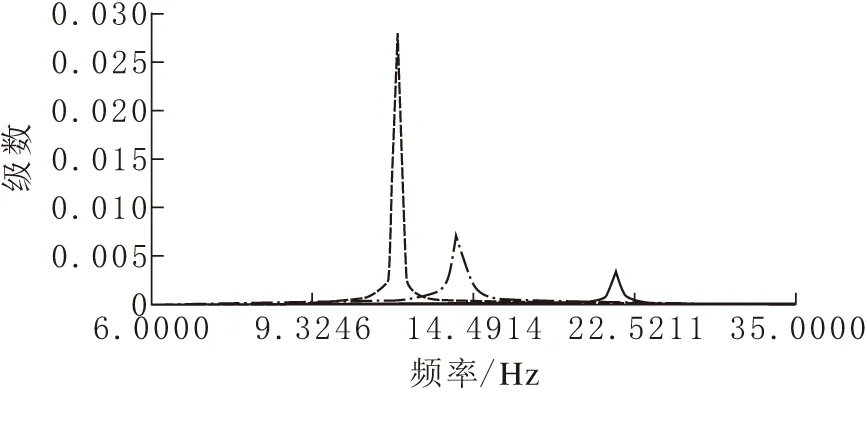
圖 7 刀具y向振動的模態參與因子

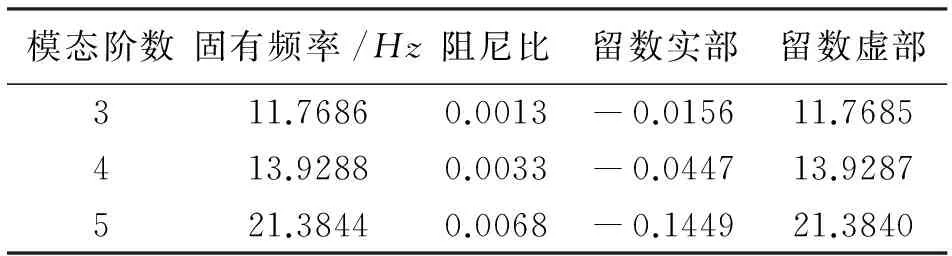
表3 第3～5階模態參數信息

在模態變形方面，由后處理結果可知，第3階模態變形為腰部、大臂、小臂繞關節1轉動，第4階模態變形為大臂、小臂繞關節2轉動，第5階模態變形為大臂、小臂繞關節2轉動且小臂繞關節3轉動，而其他階模態變形都有臂桿變形的參與。分析上述3階固有頻率與理論計算結果的誤差，一方面是因為對機器人柔體動力學方程進行了簡化，未考慮重力項、速度項的影響；另一方面，在機器人柔體動力學模型中未考慮阻尼。

5 結語

本文在前人理論分析的基礎上，首先建立了6R機器人的坐標系，然后，對機器人柔度進行了分析，建立了關節柔度及臂桿柔度模型，并結合牛頓-歐拉方法推導出了機器人柔體動力學方程；最后，運用模態理論分析了機器人的固有頻率，并在建立剛柔耦合模型的基礎上對機器人進行了仿真，驗證了理論模型的正確性。

[1] 張永貴,劉文洲,高金剛. 切削加工機器人剛度模型研究[J]. 農業機械學報,2014(08):321-327.

[2]ReinlC,FriedmannM,BauerJ,etal.Model-basedOff-lineCompensationofPathDeviationforIndustrialRobotsinMillingApplications[C]. 2011IEEE/ASMEInternationalConferenceonAdvancedIntelligentMechatronics(AIM2011)Budapest,Hungary,2011:3-7.

[3] 潘 博,孫 京,于登云. 柔性關節空間機械臂建模、控制與仿真[J]. 系統仿真學報,2010(08):1826-1831.

[4] 熊有倫.機器人技術基礎[M].武漢：華中科技大學出版社,1996:32-54.

[5] 陳玉山.6R型工業機器人關節剛度辨識與實驗研究[D].武漢：華中科技大學, 2011.

[6] 劉鴻文.材料力學[M].北京：高等教育出版社,2004:176-194.

[7] 孔令富,張世輝,肖文輝，等．基于牛頓-歐拉方法的6-PUS并聯機構剛體動力學模型[J]．機器人，2004,26(05)：395-399.

[8] 白化同,郭繼忠,屠良堯.模態分析理論與試驗.北京：北京理工大學出版社,2001:9-21.

[9] 趙欣翔.考慮關節柔性的重載工業機器人結構優化研究[D].哈爾濱：哈爾濱工業大學,2013.

[10] 王斌銳,方水光,嚴冬明.機器人手臂的剛柔耦合建模及擺動模態對比[J].中國機械工程,2012(17): 2092-2097.

[11] 武利霞,郭志平,張仕民,等. 基于ADAMS/Vibration的微型擺式內燃機的振動分析[J].噪聲與振動控制,2008(01):7-9.

[責任編校： 張巖芳]

Flexible Dynamic Modeling and Modal Analysis of 6R Rrobot

LI Yuting1，LI Bo1，YAN Rong2，PENG Fangyu2，TANG Xiaowei2，CHEN Dingfang1

(1IntelligentManufacturingandControlInstitute,WuhanUniv.ofTech. ,Wuhan430063,China；2SchoolofMechanicalSci.andEngin. ,HuazhongUniv.ofSci.andTech.,Wuhan430074,China)

The paper firstly established a link coordinate system of 6R robot according to D-H method. On the basis of the coordinate system, flexible dynamic equations for the 6R robot were then given by means of Newton-Euler method considering joint flexibility and arm flexibility. Meanwhile, natural frequencies for the flexible 6R robot were calculated with modal theories. Finally, a rigid-flexible coupling modeling was set up for the robot, and simulation analysis was made with the model, and the results proved the validity of the dynamic modeling.

joint flexibility; arm flexibility; flexible dynamics; modal theories; rigid-flexible coupling

2015-04-20

李宇庭(1993-)，男，湖北荊門人，武漢理工大學本科生，研究方向為機械設計

1003-4684(2015)04-0065-05

TP242.2

A