基于疊加原理的八開關三相逆變器全調制度范圍內兩種等效PWM算法

劉勇超 葛興來 馮曉云

(西南交通大學電氣工程學院 成都 610031)

?

基于疊加原理的八開關三相逆變器全調制度范圍內兩種等效PWM算法

劉勇超 葛興來 馮曉云

(西南交通大學電氣工程學院 成都 610031)

對八開關三相逆變器(ESTPI)兩種基于不同基本電壓矢量的全調制度范圍空間矢量脈寬調制(SVPWM)算法進行比較研究，在此基礎上，為了提高ESTPI直流電壓利用率，提出一種基于疊加原理的SVPWM過調制算法，進而得到ESTPI全調制度范圍SVPWM算法，該算法根據調制度的大小，將整個ESTPI運行區域劃分為線性調制區、過調制模式Ⅰ區和過調制模式Ⅱ區。從調制函數角度出發，基于PWM規則采樣法，推導與SVPWM算法等效的載波脈寬調制(CBPWM)算法，并得到了隨著調制度的變化，CBPWM算法調制函數的變化規律。仿真和實驗結果表明，這兩種算法作用下的輸出線電壓基波幅值與調制度呈線性關系，且最多能將其提高約10.2%。

故障重構拓撲 八開關三相逆變器 空間矢量脈寬調制 載波脈寬調制 過調制 疊加原理 調制函數

0 引言

三電平中點鉗位型(Neutral-Point-Clamped，NPC)逆變器拓撲由A.Nabea于1981年提出，與兩電平逆變器相比，其具有輸出功率大、耐壓水平高、開關過程中du/dt低、功率器件所承受的電壓應力和系統電磁干擾小以及諧波含量低等優點，已在中高壓交流傳動、交流柔性輸電系統、有源電力濾波和電力系統無功補償與吸收等多個領域得到廣泛應用[1-4]。然而由于三電平NPC逆變器系統的開關器件數量比兩電平逆變器增加了1倍，其可靠性也隨之降低[5，6]。開關器件若發生故障，逆變器將無法正常工作，對此，可借鑒容錯兩電平逆變器構造方法[7]，通過采用每相上下橋臂各串聯一個快速熔絲Fx1和Fx2(x=a，b，c)，并由雙向晶閘管VTrx連接直流側兩串聯電容中點與各橋臂中點的方式，變為容錯三電平NPC逆變器，如圖1a所示。相比于傳統容錯拓撲[8-10]只能進行開路故障重構，該拓撲在某一橋臂開關器件發生開路或短路故障時都能對拓撲進行重構，以A相橋臂為例，開關器件發生故障后可通過兩個快速熔絲迅速切除該橋臂，同時導通該相與直流側母線間的雙向晶閘管，將拓撲結構重構為如圖1b所示八開關三相逆變器(Eight-switch Three-phase Inverter，ESTPI)，進而提高故障后系統的穩定性和可靠性。

圖1 容錯三電平NPC逆變器和ESTPIFig.1 Fault-tolerant three-level NPC inverter and ESTPI

逆變器從正常運行狀態切換至單橋臂故障重構容錯運行狀態后，直流電壓利用率下降一半，逆變器的帶載能力也隨之降低[7-11]。為了維持逆變器的輸出能力，可提高直流母線電壓，但這將對器件的電壓應力和電源提出更高要求。為了在直流母線電壓不變的情況下提高單橋臂故障重構拓撲直流電壓利用率，可采用空間矢量脈寬調制(Space Vector Pulse Width Modulation，SVPWM)過調制算法[11]。基于疊加原理的SVPWM過調制算法因具有易于數字化實現、輸出基波電壓幅值與調制度呈線性關系、輸出電壓諧波含量較小等優點，已被應用于兩電平逆變器及其單橋臂故障重構拓撲四開關三相逆變器(Four-Switch Three-Phase Inverter，FSTPI)、三電平NPC逆變器和六相逆變器中[12-16]。載波脈寬調制(Carrier-based Pulse Width Modulation，CBPWM)算法采用調制波與載波直接比較的方式實現，運算量較小，易于實現，有利于高速實時運行，雖然出發點不同于SVPWM算法，但控制本質相同[13-18]。通過研究SVPWM算法與CBPWM算法的內在聯系，不僅使整合二者的優點成為可能，還有利于產生性能更優的調制算法[17]。因此，許多學者對基于疊加原理的SVPWM過調制算法等效CBPWM算法進行了研究，并取得了許多成果。從調制函數角度出發，基于PWM規則采樣法，文獻[13-15]分別推導了兩電平逆變器、FSTPI和三電平NPC逆變器基于疊加原理的SVPWM過調制算法等效CBPWM算法，然而，對于ESTPI，目前尚未有文獻對其基于疊加原理的SVPWM過調制算法及其等效CBPWM算法展開研究。

在上述文獻研究的基礎上，本文首先比較了ESTPI兩種基于不同基本電壓矢量的全調制度范圍SVPWM算法，在此基礎上，為了提高ESTPI直流電壓利用率，提出一種ESTPI基于疊加原理的SVPWM過調制算法。然后從調制函數角度出發，基于PWM規則采樣法，推導了與該SVPWM算法等效的CBPWM算法，進而得到全調制度范圍內ESTPI的SVPWM算法及其等效CBPWM算法，并歸納了該CBPWM算法調制函數的變化規律。

1 ESTPI全調制度范圍SVPWM算法

1.1 ESTPI基本工作原理

設直流母線電壓為Ud，直流側電容C1=C2，由圖1b可知，ESTPI的b、c兩相橋臂均有4個全控開關器件，4個續流二極管，2個鉗位二極管。由于鉗位二極管的作用，每相輸出P、O、N三種電平，定義b、c兩相開關函數為

(1)

式中x代表b、c兩相。

定義空間電壓矢量為

(2)

式中Uan、Ubn、Ucn分別為逆變器三相輸出相電壓。

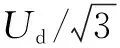
表1 ESTPI基本電壓矢量Tab.1 Fundamental voltage vectors of ESTPI

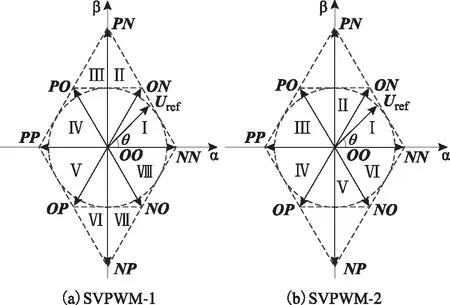
圖2 基本電壓矢量分布圖Fig.2 Diagram distribution of basic voltage vectors

1.2 兩種ESTPI全調制度范圍SVPWM算法比較

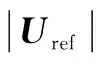
綜上所述，本文采用SVPWM-2算法，如圖2b所示，6個小矢量將兩相靜止坐標系所在平面劃分為6個扇區，在任一扇區內，參考電壓矢量Uref相鄰的2個小矢量和1個零矢量進行合成。設Uref相位角為θ，根據伏秒平衡原理可得6個扇區對應2個小矢量和零矢量的作用時間為

(3)

式中：T0、T1、T2分別為零矢量和2個小矢量的作用時間；Ts為一個調制周期；n為扇區編號。

1.3 基于疊加原理的SVPWM過調制算法

首先定義調制度m為

(4)

按照m的大小將ESTPI運行區域劃分為線性調制區(0≤m<0.907)、過調制模式Ⅰ區(0.907≤m<0.952)和過調制模式Ⅱ區(0.952≤m<1)3個區域。

在線性調制區，Uref始終位于六邊形內，當Uref端點軌跡為正六邊形內切圓時，達到線性調制區與過調制模式Ⅰ區的臨界點，此時m=0.907，進入過調制區域后，Uref超出六邊形部分不能實際輸出，因此需要對Uref的幅值或相位進行調整，根據疊加原理，可將Uref表示為兩個典型矢量的線性組合，通過調節基于m的權重系數來補償無法輸出的部分。

1)過調制模式Ⅰ區(0.907≤m<0.952)。

在過調制模式Ⅰ區內，定義過調制系數k1為

(5)

k1=0時，Uref端點軌跡為正六邊形內切圓，k1=1時，Uref端點軌跡為正六邊形邊沿。因此，在過調制模式Ⅰ區，Uref位于端點軌跡為內切圓的Usin和端點軌跡為正六邊形邊沿的Uhex之間，以Ⅰ扇區為例，二者表達式為

(6)

所以，如圖3所示，Uref可表示為權重系數為(1-k1)的Usin和權重系數為k1的Uhex的線性組合

Uref=(1-k1)Usin+k1Uhex

(7)

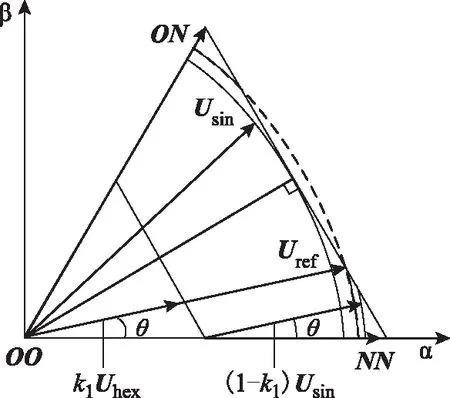
圖3 過調制模式Ⅰ區參考電壓矢量合成原理圖Fig.3 Diagram of synthetic principle of reference voltage vector in over-modulation mode Ⅰ

2)過調制模式Ⅱ區(0.952≤m<1)。

在過調制模式Ⅱ區內，同樣定義過調制系數k2為

(8)

k2=0時，Uref端點軌跡為正六邊形邊沿，k2=1時，Uref端點軌跡為正六邊形6個頂點。因此，在過調制模式Ⅱ區，Uref位于端點軌跡為正六邊形邊沿的Uhex和端點軌跡為正六邊形6個頂點的Usix之間，以Ⅰ扇區為例，Usix表達式為

(9)

同樣如圖4所示，Uref可表示為權重系數為(1-k2)的Uhex和權重系數為k2的Usix的線性組合

Uref=(1-k2)Uhex+k2Usix

(10)

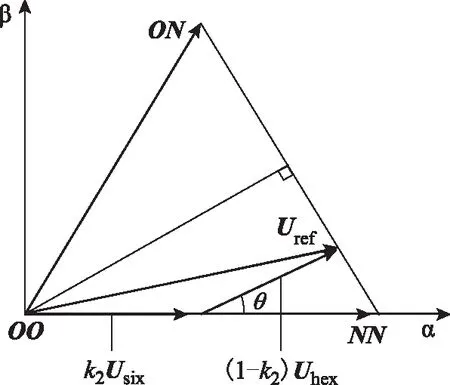
圖4 過調制模式Ⅱ區參考電壓矢量合成原理圖Fig.4 Diagram of synthetic principle of reference voltage vector in over-modulation mode Ⅱ

2 ESTPI全調制度范圍SVPWM算法等效CBPWM算法

2.1ESTPI的CBPWM算法基本原理

為了實現ESTPI的CBPWM算法，需要兩個三角載波，其基本原理如圖5所示[18]。令幅值大于零的三角載波為正三角載波，其幅值為1，小于零的為負三角載波，其幅值為-1。

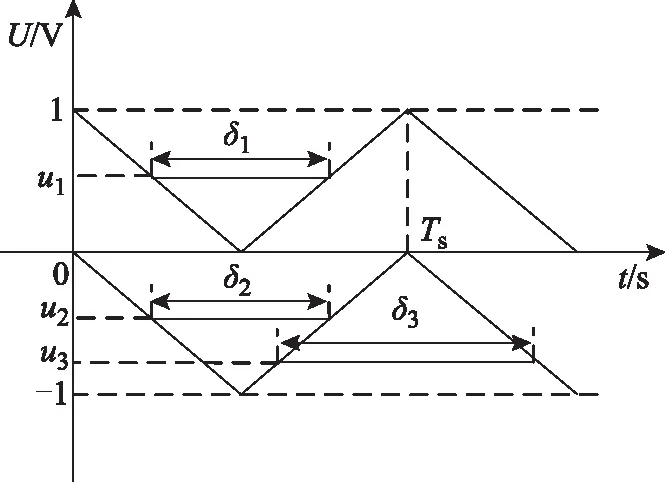
圖5 ESTPI的CBPWM算法原理圖Fig.5 The principle diagram of CBPWM algorithm of ESTPI

以b相為例，當調制波大于正三角載波時，VTb1、VTb2導通，VTb3、VTb4關斷，對應Sb=1；當調制波位于兩三角載波之間時，VTb2、VTb3導通，VTb1、VTb4關斷，對應Sb=0；當調制波大于負三角載波時，VTb3、VTb4導通，VTb1、VTb2關斷，對應Sb=-1。由此可知，VTb1的開關狀態只取決于調制波與正三角載波的相對大小，VTb4的開關狀態只取決于調制波與負三角載波的相對大小，VTb1與VTb3、VTb2與VTb4開關狀態總是相反，因此，為了方便推導SVPWM等效CBPWM算法調制函數，可采用兩路獨立的調制波，一路正調制波和正三角載波比較產生VTb1與VTb3的控制信號，一路負調制波和負三角載波比較產生VTb2與VTb4的控制信號，分別求得這兩路調制波后，再將二者合并為一路調制波，并以該調制波與兩路三角載波進行比較產生開關信號。

2.2 線性調制區等效CBPWM算法

在線性調制區，以b相為例，基于PWM規則采樣法，可得其Ⅰ扇區正負調制波為

(11)

同理可得線性調制區內6個扇區b相正負調制波為

(12)

(13)

令θ=ωt，將式(12)、式(13)合并，可得線性調制區b相調制函數表達式為

(14)

同理，基于PWM規則采樣法，可得線性調制區c相調制函數uc(t)表達式，因此ESTPI的線性調制區SVPWM算法等效CBPWM算法b、c兩相調制函數為

(15)

2.3 過調制模式Ⅰ區等效CBPWM算法

在過調制模式Ⅰ區，仍以b相為例，在Ⅰ扇區內，聯立式(6)和式(7)可得Uref為

(16)

聯立式(4)、式(16)，并代入式(11)可得Ⅰ扇區b相正負調制波為

(17)

同理可得過調制模式Ⅰ區內6個扇區b相正負調制波為

(18)

(19)

令θ=ωt，將式(18)和式(19)合并，可得過調制模式Ⅰ區b相調制函數表達式為

ub(t)=[1-k1+k1/cos(π/6-ωt*)]sin(ωt-π/3)

(20)

其中，ωt*與n的對應關系為

ωt*=ωt-(n-1)π/3

(21)

同理可得過調制模式Ⅰ區c相調制函數uc(t)表達式，因此ESTPI的過調制模式Ⅰ區SVPWM算法等效CBPWM算法b、c兩相調制函數為

(22)

2.4 過調制模式Ⅱ區等效CBPWM算法

在過調制模式Ⅱ區，同樣以b相為例，在Ⅰ扇區內，聯立式(6)、式(9)和式(10)可得Uref為

(23)

聯立式(4)和式(23)，并代入式(11)可得Ⅰ扇區b相正負調制波分別為

ub+=0

(24)

(25)

同理可得過調制模式Ⅱ區內6個扇區b相正負調制波為

(26)

(27)

令θ=ωt，將式(26)和式(27)合并，可得過調制模式Ⅱ區b相調制函數表達式為

(28)

同理可得過調制模式Ⅱ區c相調制函數表達式為

(29)

3 仿真與實驗結果

為了驗證ESTPI全調制度范圍內兩種PWM算法的可行性和等效性，利用Matlab/Simulink搭建了全調制度范圍內兩種算法的仿真模型，并基于TMS320F2812控制器和dSPACE半實物實驗平臺，進行仿真與硬件在回路實驗。仿真和實驗相關參數為：逆變器開關頻率1 000 Hz，載波比20，直流母線電壓3 000 V，直流側兩電容均為3 300 μF。ESTPI輸出線電壓基波幅值Uf及總諧波畸變因數(Total Harmonic Distortion，THD)與m的關系、不同調制度下SVPWM等效CBPWM算法調制函數分別如圖6、圖7所示。

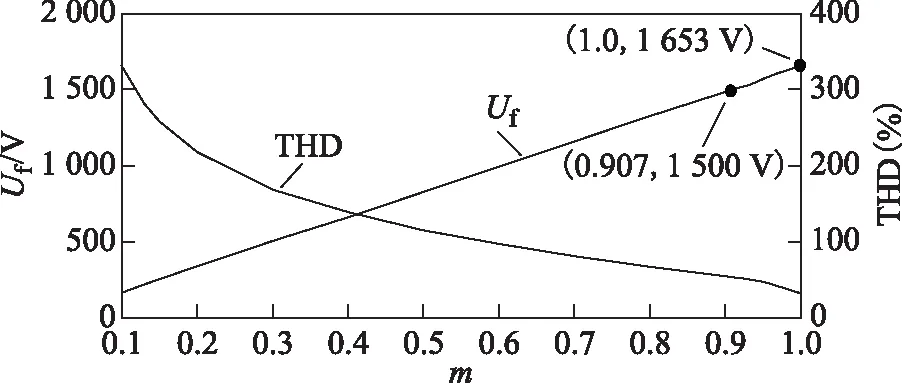
圖6 輸出線電壓基波幅值及THD與m關系圖Fig.6 Relationship between fundamental voltage amplitude and THD of output line voltage and modulation index

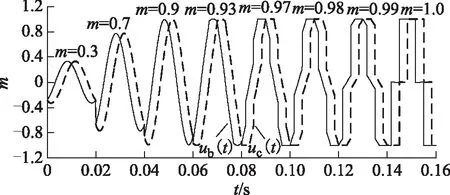
圖7 不同調制度下CBPWM算法調制函數Fig.7 Modulating functions of CBPWM algorithm with different modulation index

由圖6可知，在過調制區內，Uf與m依然保持線性關系，并通過采用該過調制算法，Uf最多可從1 500 V增加至1 653 V，提高約10.2%。此外，隨著m的增大，Uf也隨之增大，而T0則隨之減小，并在進入過調制模式Ⅱ區后降為零[13]，因此，輸出線電壓THD隨m的增大而降低。由圖7可知，雖然ESTPI是三電平NPC逆變器單橋臂故障重構拓撲，采用的基于疊加原理的SVPWM過調制算法類似于兩電平逆變器對應算法，但該算法等效CBPWM算法b、c兩相調制函數卻不同于兩電平和三電平NPC逆變器[13，15]。

在全調制范圍內，b、c兩相調制函數始終波形相同，左右對稱，相位相差π/3。在線性調制區，b、c兩相調制函數為兩個相同的正弦波，隨著m的增大，二者在保持正弦性不變的同時，峰值也隨之增大，當峰值為1時，達到線性調制區與過調制模式Ⅰ區的臨界點。m繼續增大，進入過調制模式Ⅰ區，二者失去正弦性，與此同時，將出現函數值達到1或-1的飽和區域，且隨m的增大，該區域逐漸增大，當在一個周期內，b、c兩相調制函數有1/3的區域達到飽和時，達到過調制模式Ⅰ區與過調制模式Ⅱ區的臨界點。m繼續增大，進入過調制模式Ⅱ區，飽和區域也隨之繼續增大，最后，當m增大到1，一個周期內，二者只有-1、0、1三種取值時，則進入方波區。

由前面分析可知，全調制度范圍內，線性調制區所占比重最大，為了進一步驗證線性調制區內兩種算法的等效性，m在線性調制區較低調制度范圍內取0.3，較高調制度范圍內取0.7，輸出線電壓波形、直流側電容電壓波形以及Uab和Ubc頻譜圖分別如圖8～圖13所示。m在過調制模式Ⅰ區取0.93，輸出線電壓波形、直流側電容電壓波形以及Uab和Ubc頻譜圖分別如圖14～圖16所示。m在過調制模式Ⅱ區取0.98，輸出線電壓波形、直流側電容電壓波形以及Uab和Ubc頻譜圖分別如圖17～圖19所示。方波區輸出線電壓波形、直流側電容電壓波形以及Uab和Ubc頻譜圖分別如圖20～圖22所示。

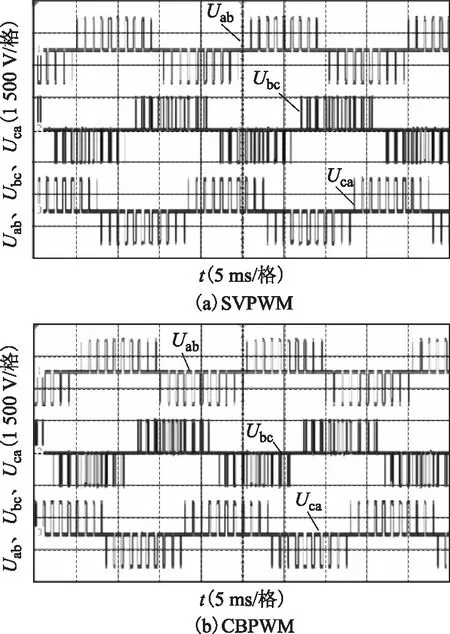
圖8 m=0.3時SVPWM與CBPWM輸出線電壓Fig.8 Output line voltage of SVPWM and CBPWM when m=0.3

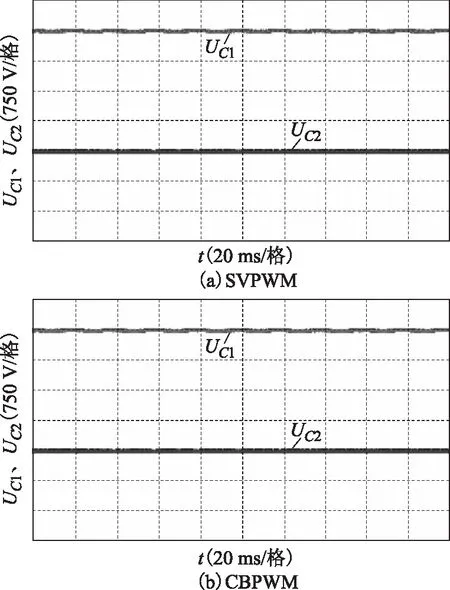
圖9 m=0.3時SVPWM與CBPWM電容電壓Fig.9 Capacitor voltageof SVPWM and CBPWM when m=0.3

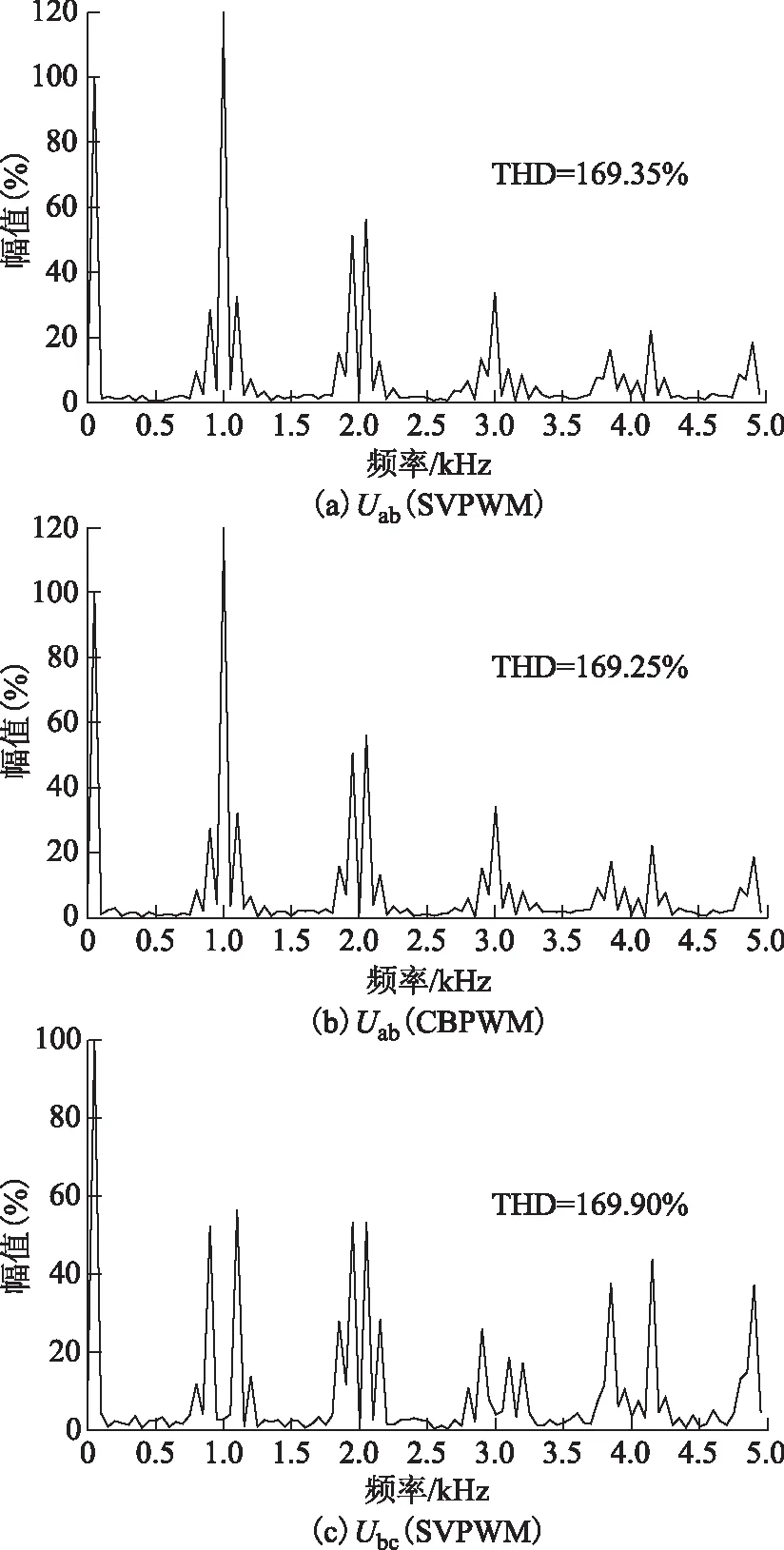
圖10 m=0.3時SVPWM與CBPWM的Uab和Ubc頻譜圖Fig.10 The FFT of Uab and Ubc of SVPWM and CBPWM when m=0.3

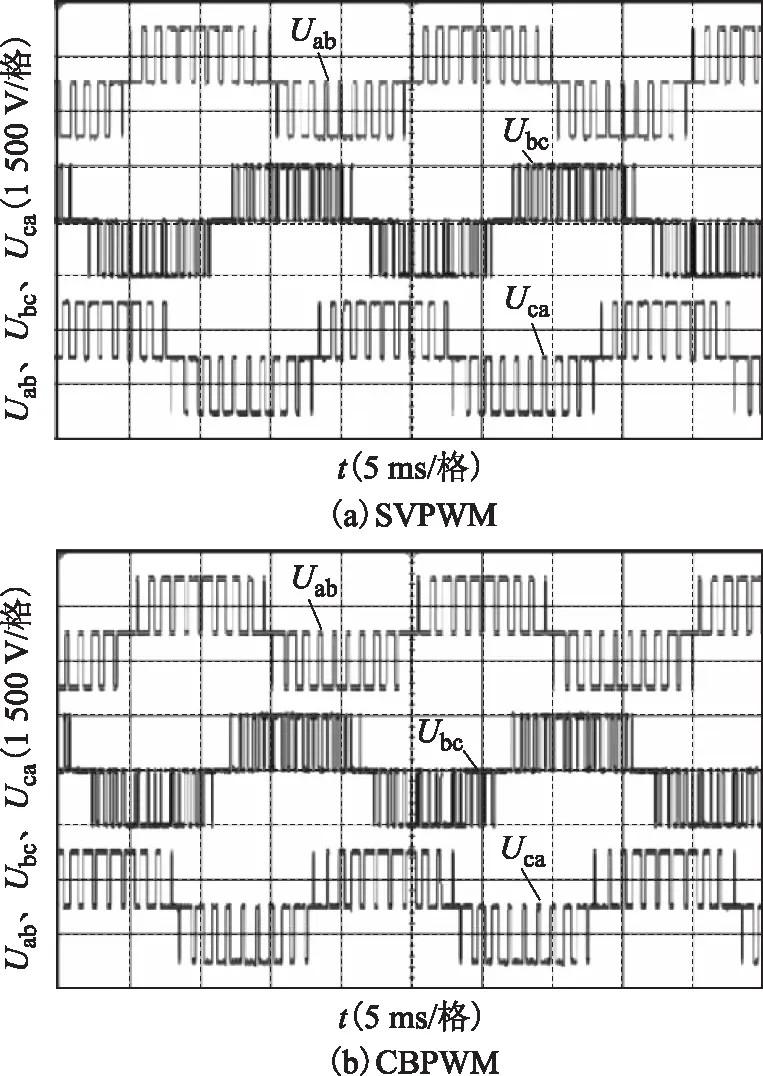
圖11 m=0.7時SVPWM與CBPWM輸出線電壓Fig.11 Output line voltage of SVPWM and CBPWM when m=0.7

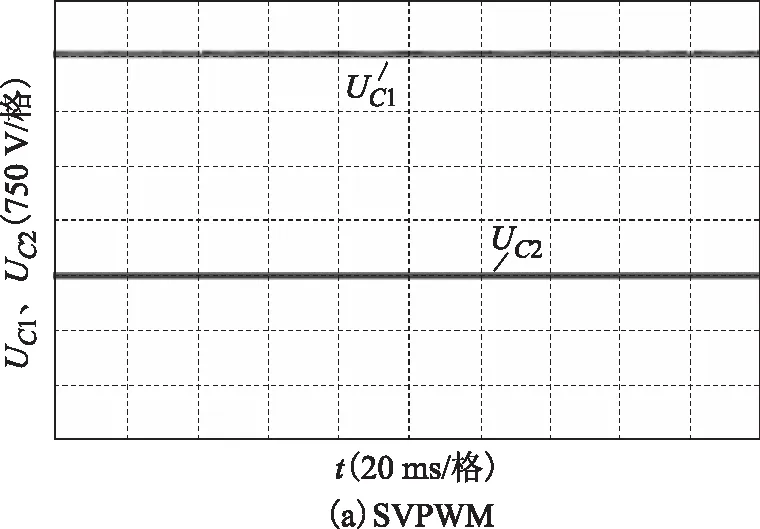
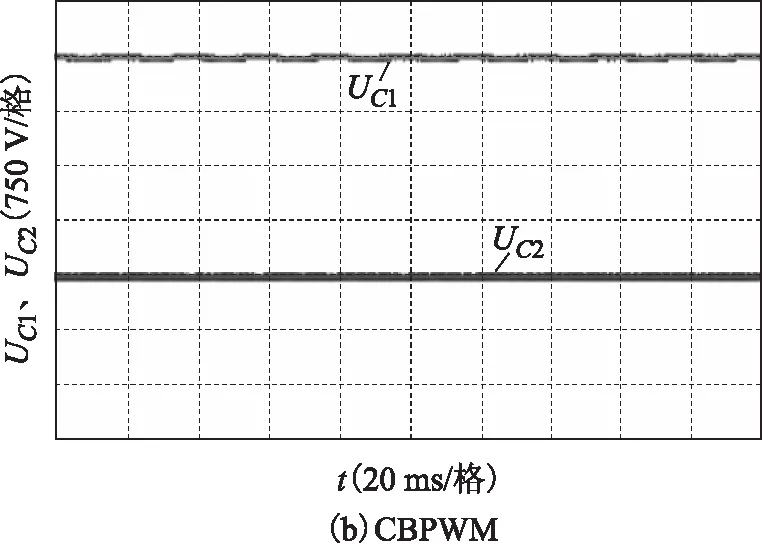
圖12 m=0.7時SVPWM與CBPWM電容電壓Fig.12 Capacitor voltageof SVPWM and CBPWM when m=0.7

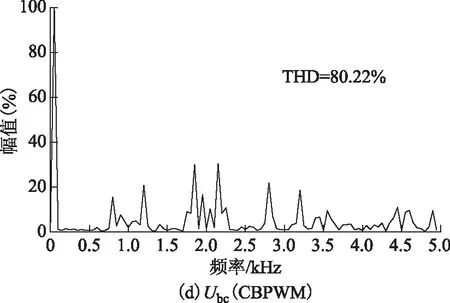
圖13 m=0.7時SVPWM與CBPWM的Uab和Ubc頻譜圖Fig.13 The FFT of Uab and Ubc of SVPWM and CBPWM when m=0.7

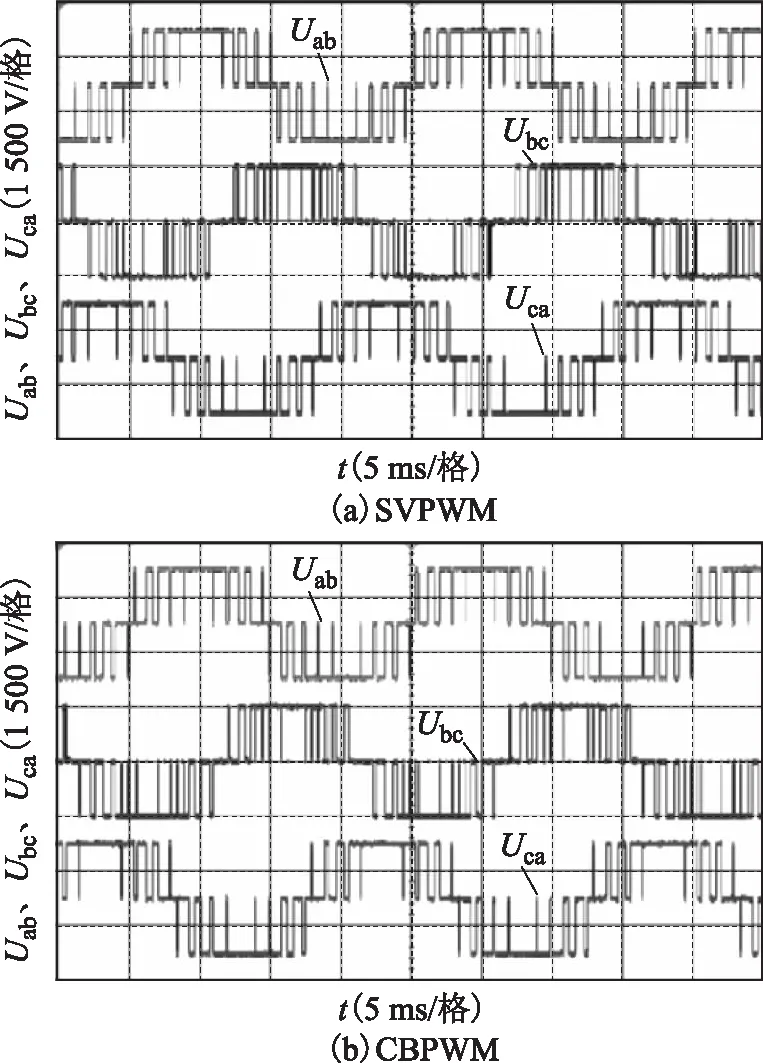
圖14 m=0.93時SVPWM與CBPWM輸出線電壓Fig.14 Output line voltage of SVPWM and CBPWM when m=0.93

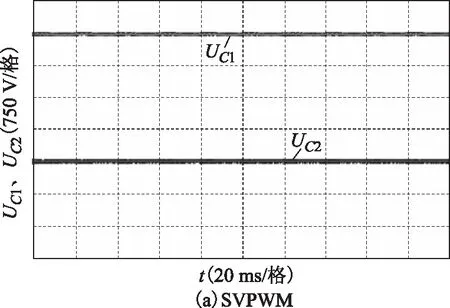
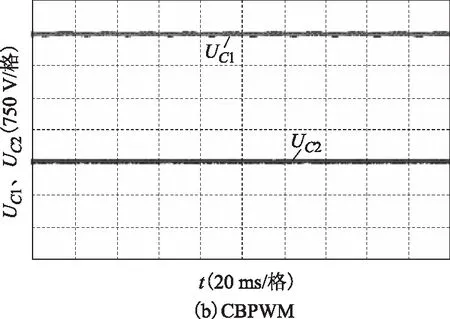
圖15 m=0.93時SVPWM與CBPWM電容電壓Fig.15 Capacitor voltage of SVPWM and CBPWM when m=0.93

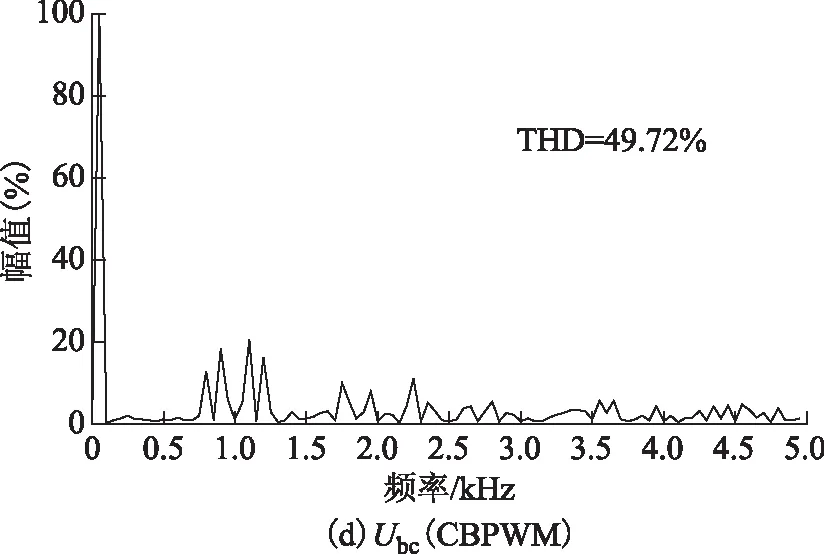
圖16 m=0.93時SVPWM與CBPWM的Uab和Ubc頻譜圖Fig.16 The FFT of Uab and Ubc of SVPWM and CBPWM when m=0.93

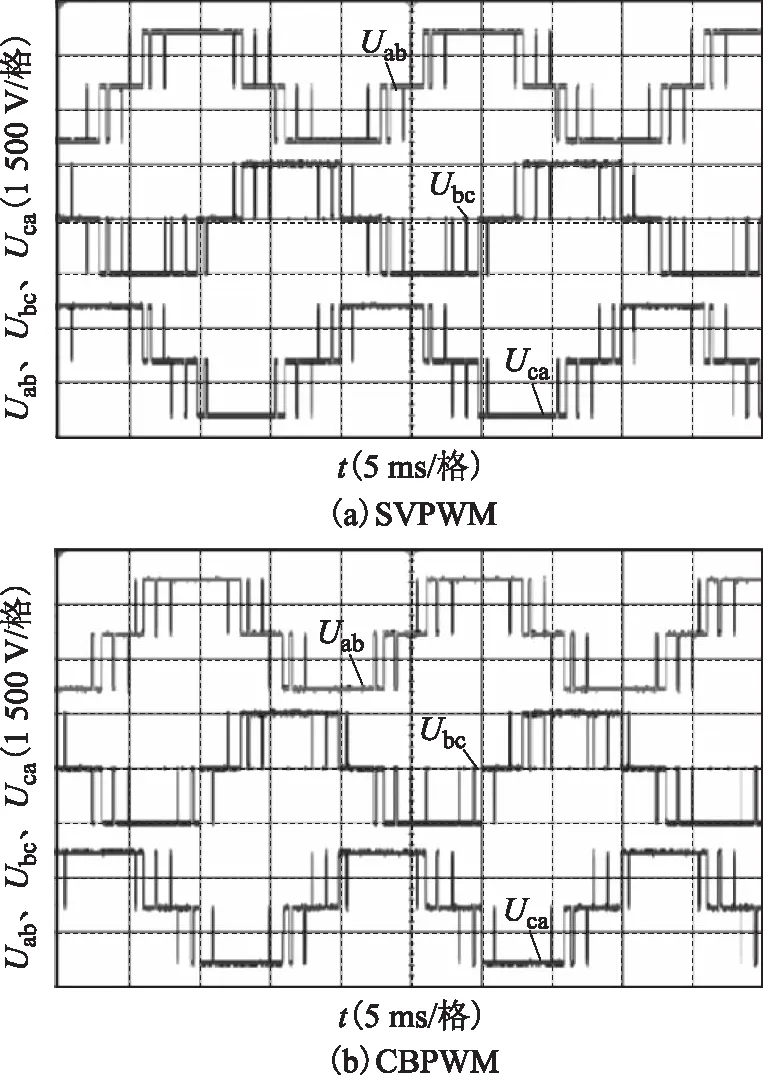
圖17 m=0.98時SVPWM與CBPWM輸出線電壓Fig.17 Output line voltage of SVPWM and CBPWM when m=0.98

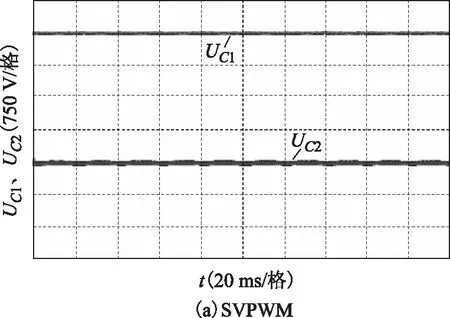
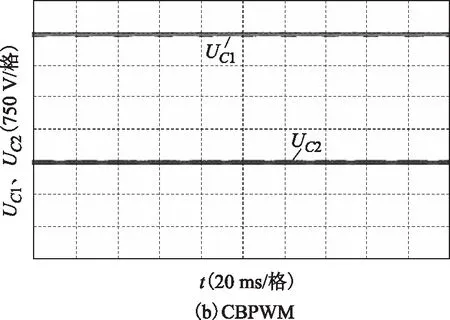
圖18 m=0.98時SVPWM與CBPWM電容電壓Fig.18 Capacitor voltage of SVPWM and CBPWM when m=0.98

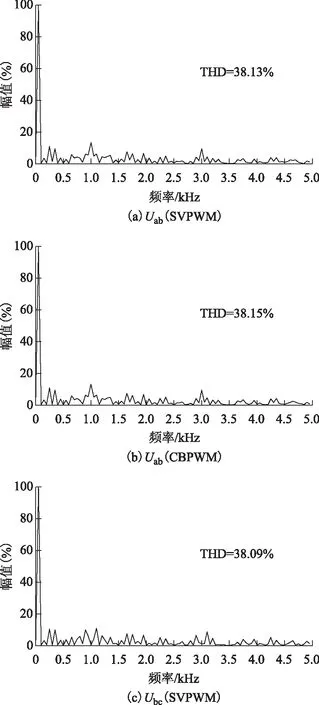
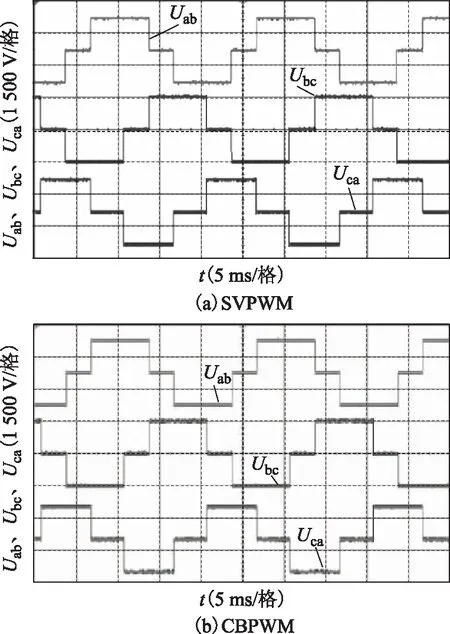
圖20 m=1.0時SVPWM與CBPWM輸出線電壓Fig.20 Output line voltage of SVPWM and CBPWM when m=1.0

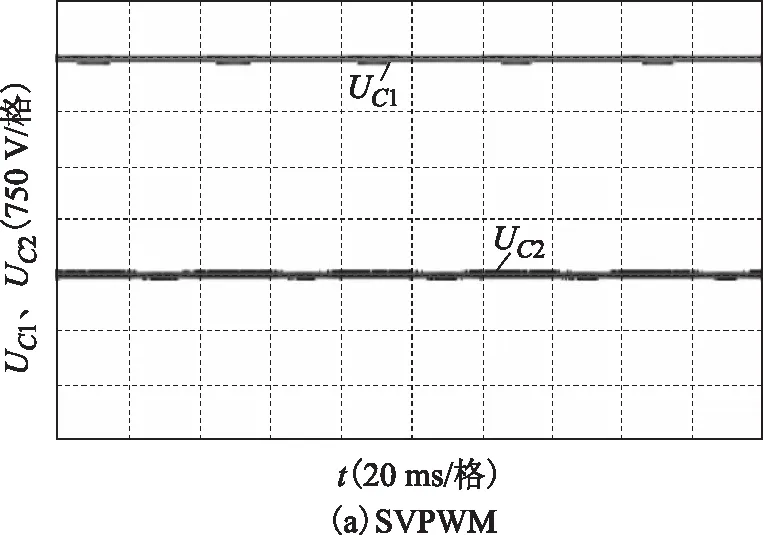
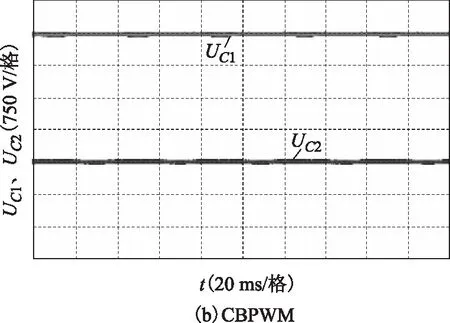
圖21 m=1.0時SVPWM與CBPWM電容電壓Fig.21 Capacitor voltage of SVPWM and CBPWM when m=1.0

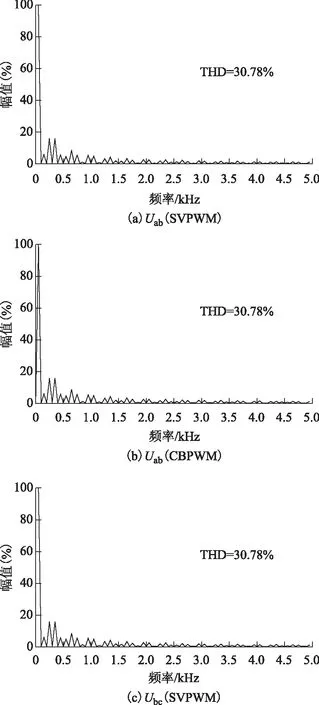
圖22 m=1.0時SVPWM與CBPWM的Uab和Ubc頻譜圖Fig.22 The FFT of Uab and Ubc of SVPWM and CBPWM when m=1.0

由圖10、圖13、圖16、圖19、圖22可知，全調制度范圍內SVPWM算法與其等效CBPWM算法諧波分布及主要諧波含量基本相同。仿真和實驗結果證明了本文提出的ESTPI全調制度范圍兩種PWM算法的等效性和有效性，二者都能夠實現從線性調制區到方波區的平滑過渡，有效提高了直流電壓利用率。

4 結論

為了提高三電平NPC逆變器單橋臂故障重構拓撲ESTPI直流電壓利用率，首先比較了其兩種基于不同基本電壓矢量的全調制度范圍SVPWM算法，并在此基礎上提出一種ESTPI基于疊加原理的SVPWM過調制算法。然后基于PWM規則采樣法，從調制函數的角度出發，推導了與該SVPWM算法等效的CBPWM算法，進而得到全調制度范圍內ESTPI的SVPWM算法及其等效CBPWM算法，并總結了隨調制度變化相應的等效CBPWM算法調制函數變化規律。這兩種ESTPI等效PWM算法都能夠實現從線性調制區到方波區的全調制度范圍的脈寬調制，且最多能提高輸出線電壓基波幅值約10.2%。

[1] Nabea A，Takahashi I，Akagi H.A new neutral-point-clamped PWM inverter[J].IEEE Transactions on Industry Applications，1981，IA-17(5)：518-523.

[2] 姜衛東，王群京，陳權，等.一種完全基于兩電平空間矢量調制的三電平空間矢量調制算法[J].電工技術學報，2009，24(1)：108-114. Jiang Weidong，Wang Qunjing，Chen Quan，et al.SVPWM strategy for three-level inverter based on SVPWM strategy for two-level inverter[J].Transactions of China Electrotechnical Society，2009，24(1)：108-114.

[3] 葛興來，馮曉云，韓坤，等.三電平牽引變流器無拍頻控制的硬件在回路實時仿真[J].電工技術學報，2014，29(8)：204-210. Ge Xinglai，Feng Xiaoyun，Han Kun，et al.Hardware-in-the-loopapplication of beat-less controlschemefor three-level traction inverter system[J].Transactions of China Electrotechnical Society，2014，29(8)：204-210.

[4] 李寧，王躍，雷萬鈞，等.三電平NPC變流器SVPWM策略與SPWM策略的等效關系研究[J].電網技術，2014，38(5)：1283-1290. Li Ning，Wang Yue，Lei Wanjun，et al.Research on equivalent between two kinds of SVPWM strategies and SPWM strategy for three-level neutral point clamped converter[J].Powersystem Technology，2014，38(5)：1283-1290.

[5] 陳丹江，葉銀忠.基于多神經網絡的三電平逆變器器件開路故障診斷方法[J].電工技術學報，2013，28(6)：120-126. Chen Danjiang，Ye Yinzhong.Fault diagnosis of three level inverter based on multi neural network[J].Transactions of China Electrotechnical Society，2013，28(6)：120-126.

[6] 陳丹江，葉銀忠，華容.基于波形實時分析的動車組三電平逆變器故障診斷技術[J].電工技術學報，2014，29(6)：106-113. Chen Danjiang，Ye Yinzhong，Hua Rong.Fault diagnosis for three-level inverter of CRH based on real-timewaveformanalysis[J].Transactions of China Electrotechnical Society，2014，29(6)：106-113.

[7] Ribeiro R L A，Jacobina C B，da Silva E R C，et al.Fault-tolerant voltage-fed PWM inverter AC motor drive system[J].IEEE Transactions on Industrial Electronics，2004，51(2)：439-446.

[8] Li S M，Xu L Y.Strategies of fault tolerant operation for three-level PWM inverters[J].IEEE Transactions on Power Electronics，2006，21(4)：933-940.

[9] Kim T J，Lee W C，Hyun D S.Detection method for open-circuit fault in neutral-point-clamped inverter systems[J].IEEE Transactions on Industrial Electronics，2009，56(7)：2754-2763.

[10]Caseiro L M A，Mendes A M S，Cruz S M A.Fault tolerance in back-to-back three-level neutral-point-clamped induction motor drives[C].7th IET International Conference on Power Electronics，Machines and Drives，Manchester，UK，2014：1-6.

[11]安群濤.三相電機驅動系統中逆變器障診斷與容錯控制策略研究[D].哈爾濱：哈爾濱工業大學，2011.

[12]樊揚，瞿文龍，陸海峰，等.基于疊加原理的SVPWM過調制算法[J].清華大學學報：自然科學版，2008，48(4)：461-464. Fan Yang，Qu Wenlong，Lu Haifeng，et al.SVPWM over-modulation algorithm based on superposition principle[J].Journal of Tshinghua University：Science and Technology，2008，48(4)：461-464.

[13]方輝，馮曉云，葛興來，等.過調制區內兩電平SVPWM與CBPWM算法的內在聯系研究[J].中國電機工程學報，2012，32(18)：23-30. Fang Hui，Feng Xiaoyun，Ge Xinglai，et al.Relationship studies between two-level SVPWM and CBPWM in the over-modulation region[J].Proceedings of the CSEE，2012，32(18)：23-30.

[14]Nguyen T D，Nguyen H M，Lee H H.Adaptive carrier-based PWM for a four-switch three-phase inverter under DC-link voltage ripple conditions[J].Journal of Electrical Engineering and Technology，2010，5(2)：290-298.

[15]方輝，吳瑕杰，宋文勝，等.過調制區內三電平SVPWM與CBPWM算法的統一性研究[J].中國電機工程學報，2015，35(8)：1993-2001. Fang Hui，Wu Xiajie，Song Wensheng，et al.Unity studies between three-level SVPWM and CBPWM in the over-modulation region[J].Proceedings of the CSEE，2015，35(8)：1993-2001.

[16]盛爽，陸海峰，瞿文龍，等.基于矢量分解和疊加原理雙三相感應電機在全調制比范圍內的PWM策略[J].中國電機工程學報，2013，33(18)：103-110. Sheng Shuang，Lu Haifeng，Qu Wenlong，et al.The PWM strategy in full modulation region for dual three-phase induction motors based on vector decomposition and superposition principle[J].Proceedings of the CSEE，2013，33(18)：103-110.

[17]Zhou K L，Wang D W.Relationshipbetweenspace- vectormodulationandthree-phasecarrier-based PWM acom-prehensive analysis three-phase inverters[J].IEEE Transactions on Industry Applications，2002，49(1)：186-196.

[18]方輝，宋文勝，馮曉云，等.三電平SVPWM與CBPWM算法的內在聯系研究[J].電工技術學報，2014，29(10)：19-27. Fang Hui，Song Wensheng，Feng Xiaoyun，et al.Relationship between three-level SVPWM and CBPWM[J].Transactions of China Electrotechnical Society，2014，29(10)：19-27.

[19]阮毅，陳伯時.電力拖動自動控制系統—運動控制系統[M].北京：機械工業出版社，2009：140.

[20]Lin B R，Wei T C.Space vector modulation strategy for an eight-switch three-phase NPC converter[J].IEEE Transactions on Aerospace and Electronic Systems，2004，40(2)：553-566.

Two Types of Equivalent PWM Algorithms in the Full Modulation Region for Eight-switch Three-phase Inverter Based on the Superposition Principle

LiuYongchaoGeXinglaiFengXiaoyun

(School of Electrical Engineering Southwest Jiaotong University Chengdu 610031 China)

At first，the comparison study on two space vector pulse width modulation (SVPWM) algorithms for eight-switch three-phase inverter(ESTPI) in the full modulation region based on different basic voltage vectors are carried out.In order to enhance the utilization ratio of the DC-link voltage of ESTPI，a SVPWM algorithm based on the superposition principle in the over-modulation region is proposed.Based on that，a SVPWM algorithm for ESTPI in the full modulation region is obtained.This algorithm divides the operation region of ESTPI into linear region，over-modulation mode I region，and over-modulation mode II region depending on the modulation index.Then，based on PWM regular sampling method，the modulating functions of the equivalent carrier-based pulse width modulation (CBPWM) algorithm of this SVPWM algorithm in the full modulation region are derived.The change rules of the equivalent carrier-based modulating functions are summarized with the modulation index changing afterwards.The simulation and experimental results show that the amplitude of fundamental line voltage is proportional to the modulation index and it can be increased maximumly by about 10.2%，by adopting these two PWM algorithms.

Post-fault reconfigured topology，eight-switch three-phase inverter，space vector pulse width modulation，carrier-based pulse width modulation，over-modulation，superposition principle，modulating function

國家自然科學基金-高鐵聯合基金重點項目(U1134205)和國家自然科學基金(51207131，51277135)資助項目。

2014-12-02 改稿日期2015-05-25

TM464

劉勇超 男，1991年生，碩士研究生，研究方向為兩電平和三電平NPC逆變器單橋臂故障重構拓撲調制與控制策略。

葛興來 男，1979年生，副教授，研究方向為電力牽引交流傳動系統控制、故障診斷及穩定性分析。(通信作者)