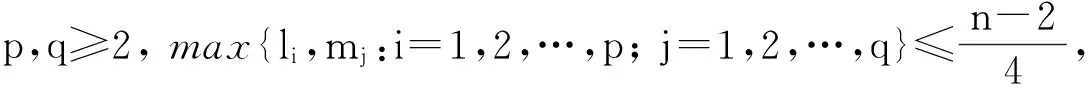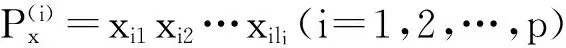兩類樹圖的Hamiltonian色數

申玉發，高 燁，王 瑩，武利猛

(河北科技師范學院數學與信息科技學院，河北 秦皇島，066004)

?

兩類樹圖的Hamiltonian色數

申玉發，高 燁，王 瑩，武利猛

(河北科技師范學院數學與信息科技學院，河北 秦皇島，066004)

一個n階連通圖G的Hamiltonian染色是從G的頂點集V(G)到正整數集(稱為顏色集)的一個映射c，使得對于G的任意2個不同的頂點u和v滿足|c(u)-c(v)|+D(u,v)≥n-1，其中D(u,v)表示G中u到v的最長路徑的長度。對一個Hamiltonian染色c，將max{c(u):u∈V(G)}稱為c的值，記作hc(c)。將min{hc(c):c是G的任意Hamiltonian染色}稱為G的Hamiltonian色數，記作hc(G)。本次研究得到了滿足max{D(u,v)|u,v∈V(G)的d-重似星樹和廣義雙星這兩類樹圖的Hamiltonian色數的確切值。

Hamiltonian染色；Hamiltonian色數；d-重似星樹；廣義雙星

2001年，Chartrand等[1,2]基于無線電臺的頻道分配問題提出了Radio-k-染色的概念。進一步，2005年，Chartrand等[3,4]又在Radio-k-染色概念的基礎上提出了Hamiltonian染色的概念。一個n階連通圖G的Hamiltonian染色是從G的頂點集V(G)到正整數集(稱為顏色集)的一個映射c，使得對于G的任意2個不同的頂點u和v滿足|c(u)-c(v)|+D(u,v)≥n-1，其中D(u,v)表示G中u到v的最長路徑的長度。對一個Hamiltonian染色c，將max{c(u):u∈V(G)}稱為c的值，記作hc(c)。將min{hc(c):c是G的任意Hamiltonian染色}稱為G的Hamiltonian色數，記作hc(G)。如果G的一個Hamiltonian染色c滿足hc(c)=hc(G)，則稱c為G的最小的Hamiltonian染色。

1 預備知識

1.1 兩類特殊樹圖的概念

似星樹以及d-重似星樹的定義由文獻[8]提出，文獻[8]中限定了d≥3。筆者從另一角度(在似星樹的定義中允許d=2)給出相應的概念，并引入標準似星樹及標準d-重似星樹的概念。

定義1 將一個頂點u0與d(d≥2)條長度分別為mi(mi≥1,i=1,2,…,d)的路Pi的一個端頂點連一條邊，所得到的樹圖稱為似星樹(或稱為廣義星)，記作S(u0:m1,m2,…,md)，并稱u0為該似星樹的根(或稱為星心)，稱路Pi(i=1,2,…,d) ()為似星樹的懸掛路。特別地，若對任意的i=1,2,…,d，均有mi=m，則稱該似星樹為標準似星樹，記作S(u0:m(d))。

定義2 設似星樹S0(u0:m1,m2,…,md)的根u0的度d≥3，在其第i(i=1,2,…,d)條懸掛路的1度頂點與一個似星樹Si(ui:m1,…,mi-1,mi+1,…,md)的根ui粘連所得到的樹圖稱為d-重似星樹，記作S(S0(u0):m1,m2,…,md)。特別地，若對任意的i=1,2,…,d，均有mi=m，即S0(u0:m1,m2,…,md)是標準似星樹S(u0:m(d))，則稱相應的d-重似星樹為標準d-重似星樹，記作S(S0(u0):m(d))。

1.2 一些引理

對于圖G的一個給定的頂點序列σ:v1,v2,…,vn，定義G的頂點集V(G)到正整數集的一個映射cσ：

cσ(v1)=1,cσ(vi+1)-cσ(vi)=(n-1)-D(vi,vi+1), 1≤i≤n-1

(1)

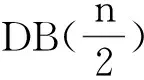
關于似星樹，建立如下引理。

引理2 在一個似星樹G=S(x;l1,l2,…,lp)中，如果

(2)

則在G-x中存在一個頂點序列σ0，使σ0中任意個相鄰頂點不在G的同一懸掛路上。

證明 記G的第i(i=1,2,…,p)條懸掛路上的頂點為xi1,xi2,…,xili。下面對G中懸掛路個數p用數學歸納法來證明。

當l1=l2時，在G-x中存在一個頂點序列σ0:x1l1,x2l2;x1(l1-1),x2(l2-1); …;x11,x21，使得σ0中任意個相鄰頂點不在G的同一懸掛路上。

當l1=l2+1時，在G-x中存在一個頂點序列σ0:x1l1,x2l2;x1(l1-1),x2(l2-1); …;x12,x21;x11，使得σ0中任意2個相鄰頂點不在G的同一懸掛路上。

令p≥3，假設引理2的結論在似星樹的懸掛路個數p=n-1時成立。當p=n時，不妨設l1≥ln≥…≥ln≥1。如果G是標準的似星樹，即l1=l2=…,=ln，則顯然在G-x中存在一個頂點序列σ0:x1l1,x2l2,…,xnln;x1(l1-1),x2(l2-1),…,xn(ln-1); …;x11,x21,…,xn1，使得σ0中任意2個相鄰頂點不在G的同一懸掛路上。否則，一定有l1-ln≥1。此時，可以經ln步如下遞歸地構造均滿足引理2條件(2)的ln個似星樹G(i)，i=1,2,…,ln。

斷言G(1)滿足引理2與之相應的條件(2)式。

2 d-重似星樹的Hamiltonian色數

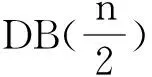
斷言1 對于G的任意頂點序列σ:v1,v2,…,vn，有

且上式等號成立當且僅當u0∈V(Pi,i+1)(i=1,2,…,n-1)，其中Pi,i+1表示從vi到vi+1的路。

事實上，由G的結構可知，對任意i(i=1,2,…,n-1) ，如果u0∈V(Pi,i+1)，則D(vi,vi+1)=D(vi,u0)+D(u0,vi+1)；否則D(vi,vi+1)

且上式等號成立當且僅當u0∈V(Pi,i+1)(i=1,2,…,n-1)。因此，斷言1成立。

斷言2 存在G的一個頂點序列σ*:v1,v2,…,vn，滿足v1=u0，vn∈N(u0)且u0∈V(Pi,i+1)(i=1,2,…,n-1)，其中Pi,i+1表示從vi到vi+1的路，使

事實上，據斷言1，如果G的一個頂點序列σ:v1,v2,…,vn滿足u0∈V(Pi,i+1)(i=1,2,…,n-1)，并且D(v1,u0)+D(vn,u0)達到它的最小值，那么D(σ)=D(G)。顯然，對G的任意一個頂點序列σ:v1,v2,…,vn，有D(v1,u0)+D(vn,u0)≥1，并且對于G的滿足v1=u0，vn∈N(u0)且u0∈V(Pi,i+1)(i=1,2,…,n-1)的每一個頂點序列σ*:v1,v2,…,vn，有D(v1,u0)+D(vn,u0)=1。

v1=u0;

…………………………………………；

vn-d+1=u0,11,vn-d+2=u0,21,…,vn=u0,d1。

推論1 對標準d-重似星樹G=S(S0(u0):m(d))，有

hc(G)=d(d3-3d+2)m2+d2(2d-3)m+d2-2d+2。

證明 根據標準d-重似星樹的定義，在定理1中對任意的i=1,2,…,d，令mi=m，即得推論1的結論。

3 非齊次廣義雙星的Hamiltonian色數

圖1 S(S0(u0):m1,m2,…,md) 圖2 S2(x:l1,l2,…,lp; y:m1,m2,…,mq)

斷言3 對于G的任意頂點序列σ:v1,v2,…,vn，有

上式等號成立當且僅當x∈V(Pi,i+1)(i=1,2,…,n-1)，其中Pi,i+1表示從vi到vi+1的路。

事實上，對任意i(i=1,2,…,n-1)，如果x∈V(Pi,i+1)，則D(vi,vi+1)=D(vi,x)+D(x,vi+1)，否則D(vi,vi+1)<(vi,x)+D(x,vi+1)，因此

且上式等號成立當且僅當x∈V(Pi,i+1)(i=1,2,…,n-1)。因此，斷言3成立。

斷言4 存在G的一個頂點序列σ*:v1,v2,…,vn，滿足v1=x，vn∈N(x)且x∈V(Pi,i+1)(i=1,2,…,n-1)，其中Pi,i+1表示從vi到vi+1的路，使得

事實上，據斷言3，如果G的一個頂點序列σ:v1,v2,…,vn滿足x∈V(Pi,i+1)(i=1,2,…,n-1)，并且D(v1,x)+D(vn,x)達到它的最小值，那么D(σ)=D(G)。顯然，對G的任意一個頂點序列σ:v1,v2,…,vn，有D(v1,x)+D(vn,x)≥1，并且對于G的滿足v1=x,vn∈N(x)且x∈V(Pi,i+1)(i=1,2,…,n-1)的每一個頂點序列σ*:v1,v2,…,vn，有D(v1,x)+D(vn,x)=1。

當t=0時，有|Vx|=|Vy|。易于發現存在G的一個頂點序列σ*:v1,v2,…,vn，其中

v1=x;v2∈Vy,v3∈Vx;v4∈Vy,v5∈Vx; …,vn-2∈Vy,vn-1∈Vx;vn=y

σ*滿足v1=x，vn∈N(x)且x∈V(Pi,i+1)(i=1,2,…,n-1)。

可見，在t≥0時，總存在G的一個頂點序列σ*:v1,v2,…,vn滿足v1=x，vn∈N(x)且vn∈N(x)(i=1,2,…,n-1)，從而有D(v1,x)+D(vn,x)=1，且

因此，斷言4成立。

注意到n=∑1≤i≤pli+∑1≤j≤qmj+2，由斷言4及引理1，有

推論2 對齊次廣義雙星G=S2(x:l(p);y:l(q))，有

hc(G)=l2(p+q)(p+q-1)+l(p-q)+1。

證明 根據齊次廣義雙星的定義，在定理2中對任意的i=1,2,…,p，j=1,2,…,q，令li=mj=l，即得推論2的結論。

[1] Gary Chartrand,David Erwin,Ping Zhang.Radio Labelings of Graphs[J].Bulletin of the ICA,2001,33:77-85.

[2] Gary Chartrand,David Erwin,Ping Zhang.A Graph Labelings Problem Suggested by FM Channel Restrictions[J].Bulletin of the ICA,2005,43:43-57.

[3] Gary Chartrand,Ladislay Nebesky,Ping Zhang.Hamiltonian Colorings of Graphs[J].Discrete Applied Mathematics,2005,146:257-272.

[4] Gary Chartrand,Ladislay Nebesky,Ping Zhang.On Hamiltonian Colorings of Graphs[J].Discrete Mathematics,2005,290:133-143.

[5] Gary Chartrand,Ladislay Nebesky,Ping Zhang.A Survey of Hamiltonian Colorings of Graphs[J].Congressus Numerantium,2004,169:179-192.

[6] R Khennoufa,O Tongi.A Note on Radio Antipodal Colourings of Paths[J].Math Bohem,2005,130:277-282.

[7] Yufa Shen,Wenjie He,Xue Li,et al.On Hamiltonian Colorings for Some Graphs[J].Discrete Applied Mathematics,2008,156(15):3 028-3 034.

[8] Wu Tingzeng,Hu Shengbiao.On the Spectral Radii ofm-Starlike Tree[J].Operations Research Transactions,2011,15(3):45-50.

[9] Béla Bollobás.現代圖論[M].北京：科學出版社,2001.

(責任編輯：朱寶昌)

Hamiltonian Chromatic Number for Two Classes of Tree Graphs

SHEN Yu-fa,GAO Ye,WANG Ying,WU Li-meng

(School of Mathematics and Information Science & Technology，Hebei Normal University of Science & Technology，Qinhuangdao Hebei，066004，China)

A Hamiltonian coloring of a connected graphGof ordernis an assignmentcof colors (positive integers) to the vertices ofGsuch thatc(u)-c(v)|+D(u,v)≥n-1 for every two distinct verticesuandvofG, whereD(u,v) is the length of a longestu-vpath inG. For an Hamiltonian coloringc, the value of isc, denoted byhc(c), while the Hamiltonian chromatic number ofGis min{hc(c):cis taken over all humiltonian colorings ofG}, denoted byhc(G). In this paper, we obtain the exact values of Hamiltonian chromatic number ford-starlike trees and generalized double stars, as two classes of tree graphs.

Hamiltonian coloring; Hamiltonian chromatic number;d-starlike trees; generalized double stars

10.3969/J.ISSN.1672-7983.2015.02.001

河北省自然科學基金項目(項目編號：A2015407063)；秦皇島市科學技術研究與發展計劃項目(項目編號：201401A038)，河北科技師范學資助計劃項目(項目編號：CXTD2012-08；2013YB008)。

2015-04-12; 修改稿收到日期: 2015-05-12

O157.5

A

1672-7983(2015)02-0001-06

申玉發(1965-)，教授，博士。主要研究方向：圖論與網絡最優化。