時標上的一類二階中立型方程正解的存在性

邸聰娜，邵香媛，王玉寬

(河北科技師范學院數(shù)學與信息科技學院，河北 秦皇島，066004)

?

時標上的一類二階中立型方程正解的存在性

邸聰娜，邵香媛，王玉寬

(河北科技師范學院數(shù)學與信息科技學院，河北 秦皇島，066004)

考慮時標上具有正負系數(shù)的二階非線性中立型動力方程正解的存在性，首先構造適當?shù)臅r標上的連續(xù)算子,再利用Banach壓縮映射原理，最后得出其正解存在的充分條件。

時標；中立型；正解；非線性

關于中立型微分方程振動性的研究，在理論上和實際應用中都有著及其重要的意義[1～4]。自從Stefan Hilger提出時標理論[5]，對導數(shù)和微分賦予了新的定義，很多學者便致力于時標上中立型方程振動性的研究[6～11]。文獻[11]中作者考慮了

正解的存在性。筆者將其推廣到非線性情況，考慮時標上具有正負系數(shù)的二階非線性中立型動力方程

(1)

其中τ(t),γi(t),δj(t)∈Crd(T,T),τ(t),γi(t),δj(t)0為常數(shù)(i=1,2,…，m，j=1,2,…,l)；m≥1,l≥1為正整數(shù)；P(t)∈Crd(T,R)且P(t)≠0，Qi,Rj∈Crd(T,R+)；fi,gj∈C(R,R)且xfi(x)>0 (x≠0)，xgj(x)>0 (x≠0)。

為了方便，本次研究假設關于t的不等式(如未說明的)是對一切足夠大的實數(shù)t成立的。并考慮如下假設：

(H1)fi(0)=0，gj(0)=0；且fi,gj均滿足Lipchitz條件，即對于某區(qū)域D，存在常數(shù)Lfi(D)>0，Lgj(D)>0，使得對?x≥0,y≥0，有|fi(x)-fi(y)|≤Lfi(D)|x-y|和|gj(x)-gj(y)|≤Lgj(D)|x-y|。

首先利用時標上的導數(shù)積分運算，鏈式法則，含參量積分求導，構造適當?shù)倪B續(xù)算子,再利用Banach壓縮映射原理，最后得出正解存在的充分條件。

1 預備知識

定義1[5]設T為時標，對t∈T，定義前跳算子σ:T→T，σ(t)=inf{s∈T:s>t}，后移算子ρ;T→T，ρ(t)=sup{s∈T：s>t}，而μ:T→[0,∞),μ(t)=σ(t)-t。如果σ(t)>t，則稱t是右疏的；而如果ρ(t)infT，ρ(t)=t，則稱t是左稠的。

定義2[5]設f：T→R，如果f在T的右稠密點連續(xù)，左稠密點存在有限極限，則稱f是rd連續(xù)的。把所有rd連續(xù)的函數(shù)組成的集合記成Crd=Crd(T)=Crd(T,R)。

2 定理及證明

假設supT=∞，且定義[t0.tif,+∞)={t∈T,t0≤t<+∞}，給出正解的存在性定理。

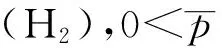
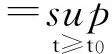
(2)

(3)

(4)

(5)

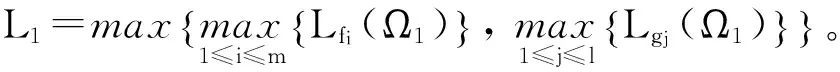
易知T1是連續(xù)的。由條件(H1)和(4)式，對?x∈Ω1及t≥t1，在此有

另一方面，由定理的條件及(2)，(5)式，可得

從而a1≤T1x≤A1。因此，T1Ω1?Ω1。又對?x1，x2∈Ω1， t≥t1,由條件(H1)及(2)，(3)式,可得

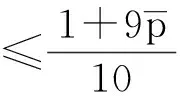
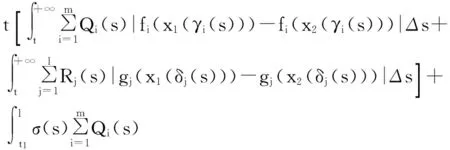
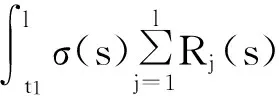
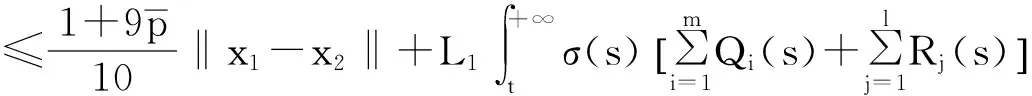
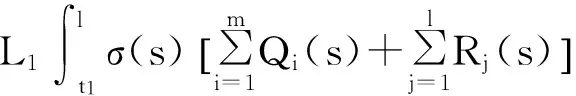
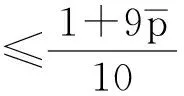
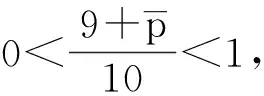
由Banach壓縮映射原理知，存在x(t)∈Ω1使得T1x(t)=x(t)，將T1x(t)=x(t)代入方程(1)計算得，x(t)就是方程(1)的一個最終正解。證畢。

定理2 若方程(1)滿足條件(H1)和(H2)，并且存在兩個常數(shù)p1,p2，使得1≤p1≤P(t)≤p2<+∞，則方程(1)一定存在一個最終正解。

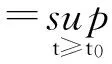
(6)

(7)

(8)

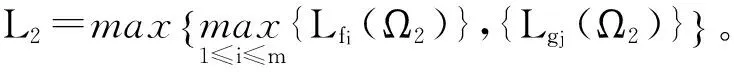
易知T2是連續(xù)的，由定理條件及(6)式，對?x∈Ω2， t≥t2，有

另一方面，由定理條件及(7)式得

從而a2≤T2x≤A2，因此T2Ω2?Ω2。又對?x1, x2∈Ω2， t≥t2，由條件(H1)及(8)式，可得

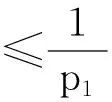
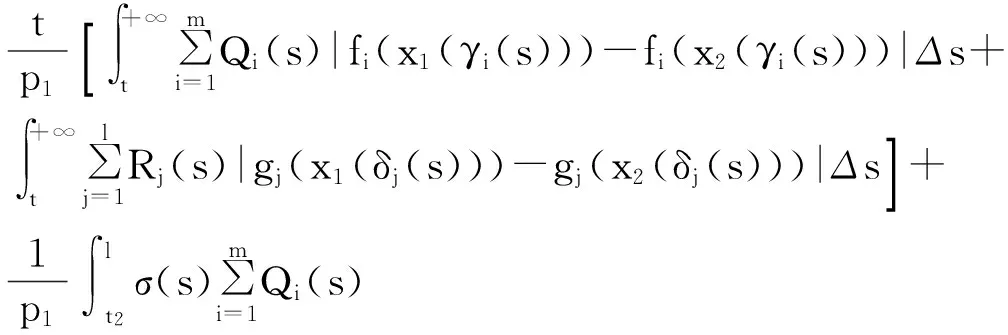
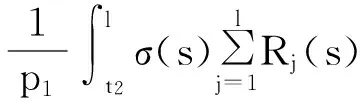
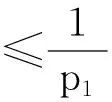
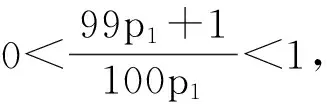
由Banach壓縮映射原理知,存在x(t)∈Ω2使得T2x(t)=x(t)，將T2x(t)=x(t)代入方程(1)計算得，x(t)就是方程(1)的一個最終正解。證畢。

注：對于-1

3 結 論

本次研究將文獻[11]中的二階中立型方程推廣到非線性方程，利用Banach壓縮映射原理，得到非線性方程非振動的充分條件，完善了時標上中立型方程的非振動性理論。

[1] L H Erbe,W K Kong,B G Zhang.Oscillatory theory for functional differential equation[M].New York：Dekker,1995.

[2] ZHANG Zhen-guo,YANG Ai-jun,DI Cong-na.Existence of positive solutions of second-order nonlinear neutral differential equations with positive and negative terms[J].JOURNAL OF APPLED MATHEMATICS and COMPUTION,2007,25:245-253.[3] YU Yuan-hong,WANG Hong-zhou.Non-oscillatory solutions of second-order non-linear neutral delay equations[J].J Math Anal App1,2005,311:445-456.

[4] LI W.Positive solutions of second-order nonlinear differential equations[J].J Math Anal App1,1998,211:326-337.

[5] Bohner M,Peterson A.Dynamic Equations on Time Scales:An Introduction with Applications[M].Boston:Birkh?user,2001.

[6] 陳大學,劉潔純.具有分布時滯的二階非線性中立型時標動力方程的振動定理[J].系統(tǒng)科學與數(shù)學,2010,30(9):1 191-1 205.

[7] 楊軍,陳雁東,張忠軍,等.時標上具有正負系數(shù)的中立型時滯動力方程的穩(wěn)定性[J].黑龍江大學自然科學學報,2012,29(2):160-164,168.

[8] 楊紅玉,葛琦,余秀萍，等.二階時標非線性中立型動力學方程的振動性[J].數(shù)學的實踐與認識,2008,38(18):253-256.

[9] Liuailian,Wuhongwu,Zhsiming.Oscillation nonautonomous neutral dynamic delay equations on time scales[J].Acta Mathematica Scientia,2006,26B(1):99-106.

[10] Ravi P Agarwal,Donal O’Regan,S H Saker.Oscillation Criteria for Second-Order Non-linear Neutral Delay Dynamic Equations[J].Mathematical Analysis and Applications,2004(300):203-217.

[11] 邸聰娜,李民良,郭雅彩，等.時標上具有振動系數(shù)的中立型動力方程非振動解的存在性[J].河北科技師范學院學報,2010,24(1):50-53.

(責任編輯：朱寶昌)

The Existence of Positive Solution for Second-order Neutral Dynamic Equations on Times Scales

DI Cong-na,SHAO xiang-yuan,WANG Yu-kuan

(School of Mathematics and Information Science & Technology,Hebei Normal University of Science & Technology,Qinghuangdao Hebei,066004,China)

This paper studied the existence of non-oscillatory solutions for the second-order nonlinear dynamic equations with the positive and negative coefficients. By defining continuous operators and using Banach fixed theorem on the time scales, the sufficient condition of the existence of positive oscillatory solutions for the above equations is obtained.

time scales；neutral term；positive solution；non-linear

10.3969/J.ISSN.1672-7983.2015.02.007

秦皇島市科學技術局秦皇島市軟科學研究計劃項目(項目編號：201302A250)。

2015-04-12; 修改稿收到日期: 2015-05-26

O175.13

A

1672-7983(2015)02-0031-05

邸聰娜(1983-)，女，講師，碩士。主要研究方向：微分方程的穩(wěn)定性與振動性。