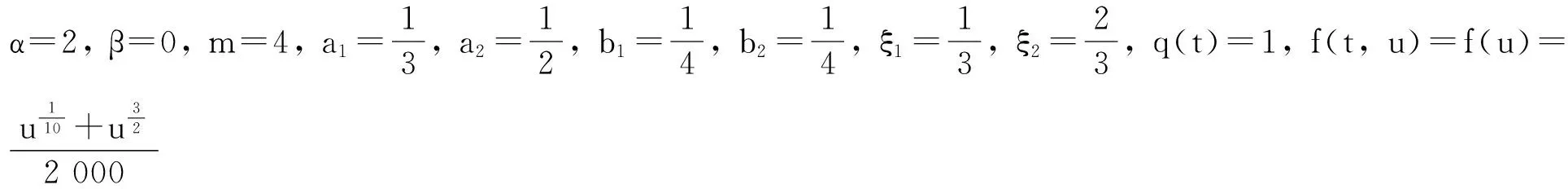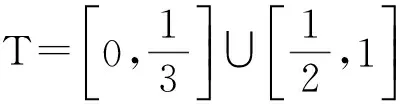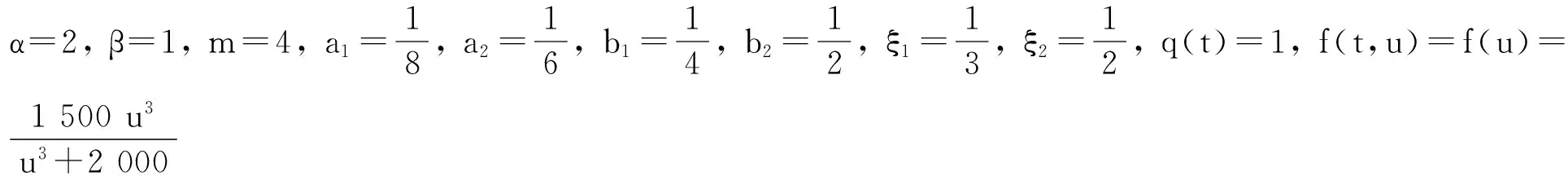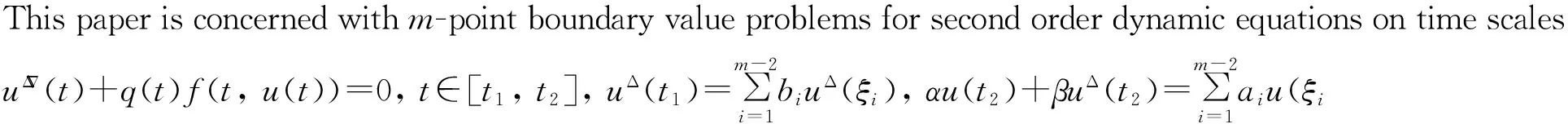時標上二階動力方程m點邊值問題的正解
武利猛,張 娟,申玉發,鄭國萍,楊曉靜
(1 河北科技師范學院數學與信息科技學院,河北 秦皇島,066004;2 河北科技師范學院科研處)
?
時標上二階動力方程m點邊值問題的正解
武利猛,張 娟,申玉發,鄭國萍,楊曉靜
(1 河北科技師范學院數學與信息科技學院,河北 秦皇島,066004;2 河北科技師范學院科研處)

時標;邊值問題;正解
近年來,時標作為數學的一個新研究分支已引起了許多學者的廣泛關注。一方面,它統一和推廣了現有的微分方程和差分方程的理論;另一方面,時標上動力方程的研究對于刻畫真實現象和過程的數學模型有著重要應用。例如:時標上的種群動力學、流行病模型、金融消費過程的數學模型等。 越來越多的學者對在時標上利用不動點定理解決動力方程的邊值問題產生了很大興趣[1~7]。目前,關于時標上二階混合導數動力方程m點邊值問題正解存在性的文章并不多見[8,9]。筆者借助于Guo-Krasnosel'skii不動點定理和Leggett-Williams不動點定理得到了至少存在2個正解和3個正解的判別條件,其中本次研究所討論的邊值問題在方程類型上有別于文獻[8,9],所得結果推廣了文獻[3]的研究結果。
本次將研究時標T上具有混合導數的動力方程m點邊值問題
(1)
(2)
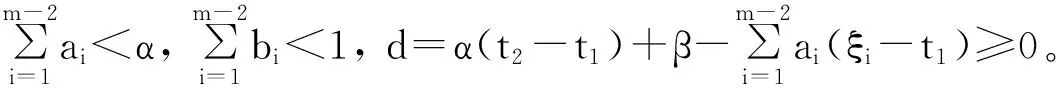
假設下列條件成立
(H1) q(t)∈Cld([t1,t2],[0,∞)),且存在t0∈[t1,t2],使得q(t0)>0。
(H2) f:[t1,t2]×[0,∞)→[0,∞)連續,且在T的任意一個包含t0的子集上f(t,·)>0。
在給出主要結果之前,先介紹一些基本定義和引理。
定義1 令Banach空間E=Cld[t1,t2]且范數‖u‖=supt∈[t1,t2]|u(t)|,定義錐P?E,且P={u∈E|u在[t1,t2]中是凹的,非增且非負}。

(A1) ‖Au‖≤‖u‖,?u∈K∩?Ω1,且‖Au‖≥‖u‖,?u∈K∩?Ω2
或者
(A2) ‖Au‖≥‖u‖,?u∈K∩?Ω1,且‖Au‖≤‖u‖,?u∈K∩?Ω2
引理2[3](Leggett-Williams不動點定理) 令P是實Banach空間E中的錐。定義
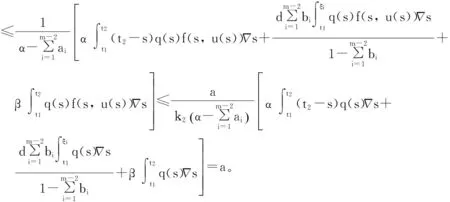
Pr={u∈P:‖u‖ (B1) {u∈P(ψ,q,l);ψ(u)>q}≠φ,且對于u∈P(ψ,q,l), ψ(Au)>q。 (B2) ‖Au‖ (B3) ψ(Au)>q,對于u∈P(ψ,q,r)且‖Au‖>l。 為了研究邊值問題(1),(2),首先研究如下形式的線性m點邊值問題 (3) (4) 引理3 如果h(t)∈Cld(T,R),那么邊值問題(3),(4)有唯一解 (5) 證明 對式(3)從t1到t進行積分,得到 (6) 再對式(6)從t1到t進行積分,得到 (7) 令t=ξi,t2分別代入式(6),有 (8) (9) (10) 令t=ξi,t2分別代入式(7),可得 (11) (12) (13) 將式(10),(13)代入式(7),可以在[t1, t2]得到式(5)。 證明 由uΔ(t)=h(t)≤0, 得到u(t)在[t1, t2]是凹的,那么uΔ(t)是遞減的。uΔ(ξi)≤uΔ(t1), i=1,2,…m-2, 由式(3) 知 引理5 如果u∈P,則 (14) 易知邊值問題(1),(2)有解, u=u(t)當且僅當u是算子方程的不動點。 則邊值問題(1),(2)至少有2個正解u1(t)和u2(t),使得0≤‖u1(t)‖≤p1≤‖u2(t)‖。 證明 由條件(H1),(H2),引理4和引理5可知AP?P。容易驗證A:P→P是全連續映射。設Ω1={u∈E:‖u‖ 則由(i)可知 從而可知‖Au‖≥‖u‖, u∈P∩?Ω1。 首先,工具便利引發民意浪潮。新媒體平臺上“人人都是發言人”,對政策的態度和情緒能夠隨時隨地“漂入”政治流中,而數據庫的存在進一步使得這些民意在短期內不會“漂出”,決策者需要時可以進行批量采集和提取,為政策變遷提供民意依據和參考。因此,新媒體工具大大增強了公眾參與政策討論的效能感,網絡民意不斷涌現。在本研究采集的500條微博文本中,有43條微博反映了普通公民的政策意向,占“政策觀點”類樣本總量的37.5%,遠遠高于傳統媒體中民意表達的數量占比。 設Ω2={u∈E:‖u‖ 令Ω3={u∈E:‖u‖<λR},選取u∈P且‖u‖=λR,有 綜上討論可知邊值問題(1),(2)至少有2個正解u1(t)和u2(t),使得0≤‖u1(t)‖≤p1≤‖u2(t)‖。 證畢。 推論1 假設下列條件成立: (C1) f0=f∞=∞; 則邊值問題(1),(2)至少有2個正解u1(t)和u2(t),使得0≤‖u1(t)‖≤p1≤‖u2(t)‖。 定理2 假設條件(H1),(H2)成立, 0 則邊值問題(1),(2)至少有3個正解u1(t), u2(t), u3(t)使得‖u1‖ 由bλ∈P(ψ,b,bλ)且ψ(bλ)=bλ>b,{u∈P(ψ,b,bλ):ψ(u)>b}≠φ,選取u∈P(ψ,b,bλ),則b≤u(ξm-2)≤u(t)≤‖u(t)‖≤bλ, t∈[t1, ξm-2]。 由條件(ii),當t∈[t1, ξm-2]得 由條件(iii)可知,當‖u‖≤a得 從而可知引理2中的條件(B2)成立。 例1 令T=[0,1]∪[2,3]考慮邊值問題 (15) (16) (17) (18) [1] Bohner M,Peterson A.Dynamic Equations on Time Scales:an Introduction with Applications[M].Boston:Birkh?user,2001.[2] Bohner M,Peterson A.Advances in Dynamic Equations on Time Scales[M].Boston:Birkh?user,2003. [3] Ismail Y.Existence of positive solutions for nonlinear three-point problems on time scales[J].Journal of Computational and Applied Mathematics,2007,206(2):888-897. [4] Han W,Liu M X.Existence and uniqueness of a nontrivial solution for a class of third-order nonlinearp-Laplacianm-point eigenvalue problems on time scales[J].Nonlinear Analysis,2009,70(5):1 877-1 889. [5] Sun H R,Li W T.Multiple positive solutions forp-Laplacianm-point boundary value problems on time scales[J].Applied Mathematics and Computation,2006,182(1):478-491. [6] Sun J P.Twin positive solutions of nonlinear first-order boundary value problems on time scales[J].Nonlinear Analysis,2008,68(6):1 754-1 758. [7] Song C X,Weng P X.Multiple positive solutions forp-Laplacian functional dynamic equations on time scales[J].Nonlinear Analysis,2008,68(2):208-215. [8] Liang S H,Zhang J H,Wang Z Y.The existence of three positive solutions ofm-point boundary value problems for some dynamic equations on time scales[J].Mathematical and Computer Modelling,2009,49:1 386-1 393. [9] Liu J,Sun H R.Multiple Positive Solutions form-Point Boundary Value Problem on Time Scales[DB/OL].(2010-08-10)[2015-06-30].http://www.boundaryvalueproblems.com/content/2011/1/591219. (責任編輯:朱寶昌) Positive Solutions tom-point Boundary Value Problems for Second Order Dynamic Equations on Time Scales WU Li-meng1, ZHANG Juan2, SHEN Yu-fa1, ZHENG Guo-ping1,YANG Xiao-jing1 (1 School of Mathematics and Information Technology, Hebei Normal University of Science & Technology, Qinhuangdao Hebei, 066004;2 Office of Science and research, Hebei Normal University of Science & Technology; China) time scales; boundary value problem; positive solutions 10.3969/J.ISSN.1672-7983.2015.02.005 國家自然科學基金項目(項目編號:11171113,11401385);河北省自然科學基金項目(項目編號:A2015407063);秦皇島市科學技術研究與發展計劃項目(項目編號:201401A038);河北科技師范學院博士基金資助項目(項目編號:2013YB008)。 2015-05-18; 修改稿收到日期: 2015-06-24 O A 1672-7983(2015)02-0020-07 武利猛(1983-),男,博士,講師。主要研究方向:微分方程理論。
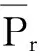
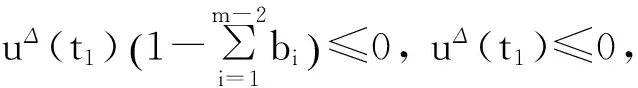
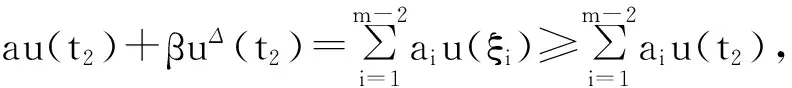
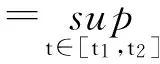
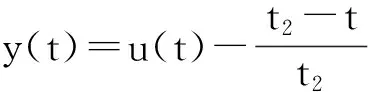
2 主要結果

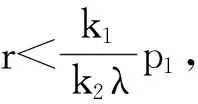
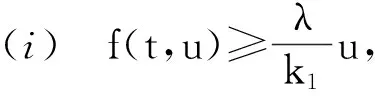
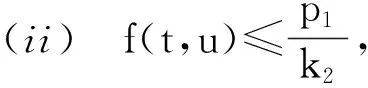
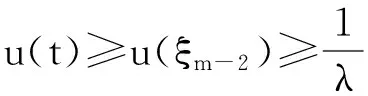
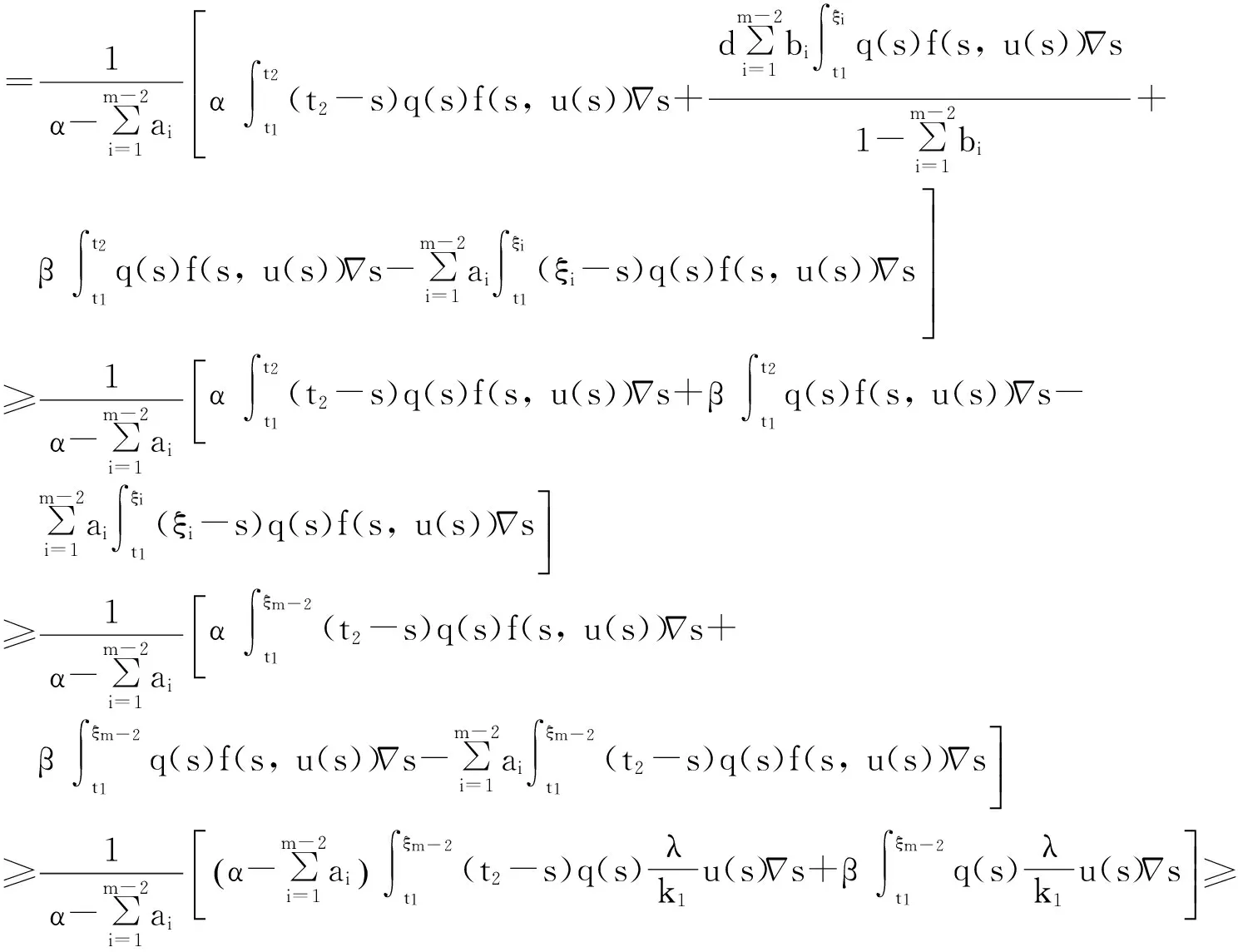

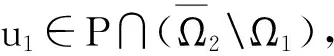
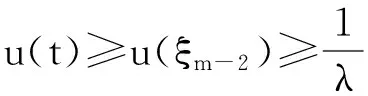
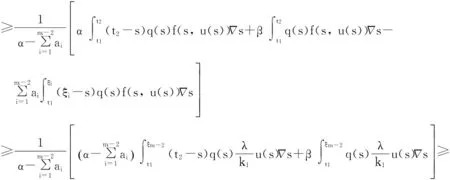
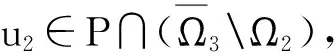
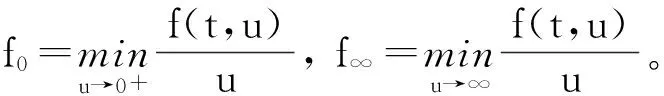
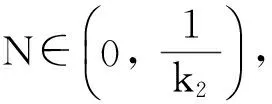

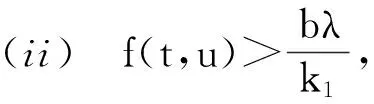
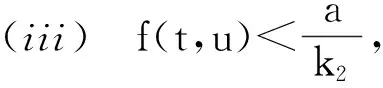
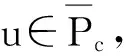
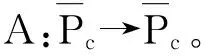


3 應用舉例