基于同態加密技術的安全多方乘積協議

夏 超 ，仲 紅 ，2，石潤華 ，2

1.安徽大學 計算機科學與技術學院，合肥 230601

2.安徽大學 計算與信號處理教育部重點實驗室，合肥 230039

1 引言

安全多方計算[1-2]（Secure Multi-party Computation，SMC）主要研究網絡環境下互不信任參與方之間的協作計算問題。通常有多個成員參與協作計算，但目前安全多方計算問題多數局限在兩方安全計算問題[3-4]的研究中。文獻[5]總結了部分特殊的安全兩方計算問題，包括安全兩方科學計算、安全兩方幾何計算、安全兩方統計分析等，并指出了多方計算協議由兩方協議推廣得到的方法。雖然安全多方計算問題的研究取得了一定的成果[6-7]，但是特殊的安全多方計算協議距離應用需求還有很大的差距。安全多方乘積（SMC）正是這樣的一類特殊安全多方計算問題。

安全多方乘積作為SMC最基本的運算之一，近年來得到了廣泛的關注。文獻[8]將一般的多方求積問題轉化成求和問題；在此基礎上，文獻[9]給出一個安全兩方乘積協議并應用到除法協議中；文獻[10]提出基于簽名技術的安全多方乘積協議，可有效地防止攻擊者對信息的篡改；文獻[11]將普通的數量乘法擴展到矩陣乘法，提出了多方安全矩陣乘積協議并應用到求解線性方程組、矩陣特征值的SMC協議中。現有這些協議因采用茫然傳輸技術[12]，協議無須第三方的參與，安全性高，在秘密分享、科學計算等安全多方計算領域中具有重要價值。但是，這些多方乘積協議都是由兩方協議的擴展得到的，參與方兩兩之間需要頻繁通信，造成協議的通信代價高；而利用茫然傳輸技術的數據量大，造成了網絡帶寬消耗大，協議的執行效率低等問題。

多方參與的協作計算中，通信代價是衡量協議性能的重要因素。本文利用同態加密技術，在半誠實模型下，設計了適用于不同通信環境下的串行和并行的安全多方乘積協議。比如，在這樣的復雜通信環境中：參與方Alice計算一個中間數據時間為1，而Alice與其他參與方通信一次的時間要遠遠超過1。此時，參與方之間如果頻繁的通信會造成較高的通信代價，不利于協議執行。選擇通信輪次少的串行協議可有效的降低通信代價；相反，如果參與方之間通信一次的時間接近或小于1，通信環境較為理想的時候，并行協議能有效地減少參與方的等待時間，提高協議執行效率。

2 預備知識

2.1 同態加密

設加密算法為E(·)，解密算法為D(·)，明文空間M∈Z。如果對任意明文x，y∈M，x+y∈M，不存在多項式時間算法區分E(x)和E(y)，且對任意k∈Z，滿足E(x+y)=E(x)E(y)，E(kx)=E(x)k，那么此算法是加同態加密算法。Paillier算法[13]就是這樣的一個算法。

2.2 Paillier算法

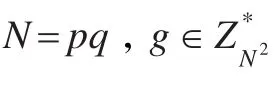
加密：任意明文m∈Zn，隨機選擇r∈Z*N，那么密文c=gmrNmodN2。

解密：解密密文c得到明文m=L(cλ(N)modN2)/L(gλ(N)modN2)。

2.3 半誠實模型下的安全性

本文假定各參與方是半誠實的，其安全性定義與文獻[14]相同，即n個參與方P1，P2，…，Pn，他們各自擁有xi，在不泄露各自任何信息的情況下合作計算多項式時間函數：

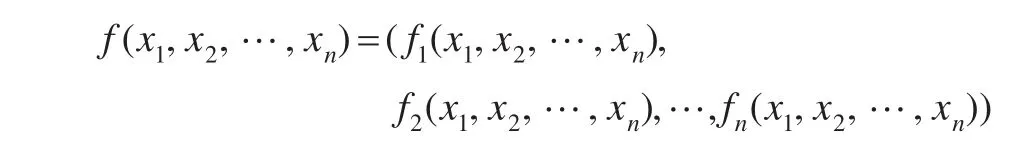
其中fi(x1，x2，…，xn)表示第i個分量。設計算f的協議標記為π，那么Pi(i=1，2，…，n)在執行協議π后得到的視圖(x1，x2， …xn)=(xi，ri，vi，1，vi，2， …，vi，m) ，其中ri是Pi隨機選擇的結果，vi，j表示Pi接收到的第j個消息。協議執行后，Pi得到的輸出序列為(x1，x2，…，xn)。

上述各方Pi(i=1，2，…，n)執行協議π能夠安全地計算出f，當且僅當下面的多項式時間算法Si(i=1，2，…，n)成立，即：

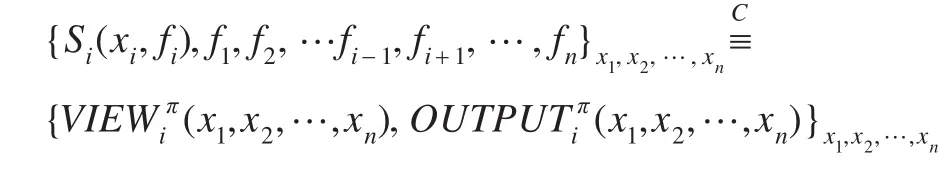
3 安全多方乘積協議

3.1 問題描述

假設有n個參與方Pi(i=1，2，…，n)，每個參與方Pi擁有一個秘密整數xi。所有參與方希望在不泄露各自秘密的前提下，計算出所有xi的乘積并且由參與方共享計算結果。

3.2 相關符號說明

RANDOM SELECTr1，r2，…，rn，表示選擇隨機n個整數r1，r2，…，rn；

x→y，表示將變量x賦值給變量y；

SEND(Alice，Bob，s1，s2，…，sn)，表示 Alice將信息s1，s2，…，sn發送給Bob；

Alice COMPUTE，表示Alice進行計算；

Alice GETs，表示Alice獲得信息s。

3.3 具體協議

以下給出串行和并行安全多方乘積協議的詳細步驟，數據傳輸流程分別如圖1、圖2所示。

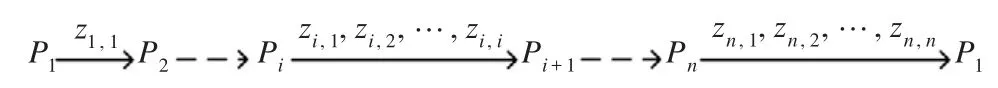
圖1 串行協議數據傳輸流程

圖2 并行協議數據傳輸流程

協議1串行的安全多方乘積協議

輸入：參與方Pi(i=1，2，…，n)擁有整數xi，Pi選擇2.2節Paillier算法并產生公私鑰(pki，ski)。

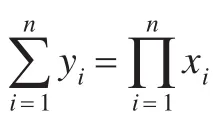
協議步驟如下：

協議1中，參與方Pi存在等待時間，改變協議的執行規則，得到協議2。

協議2并行的安全多方乘積協議

輸入：參與方Pi(i=1，2，…，n)擁有整數xi，Pi選擇2.2節Paillier算法并產生公私鑰(pki，ski)。

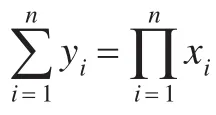
協議步驟如下：

3.4 協議分析

本節主要針對協議1和協議2的正確性、安全性和效率進行分析。

3.4.1 協議1的性能分析

正確性證明：

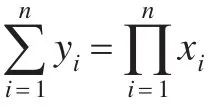
證明 在協議1步驟2中：

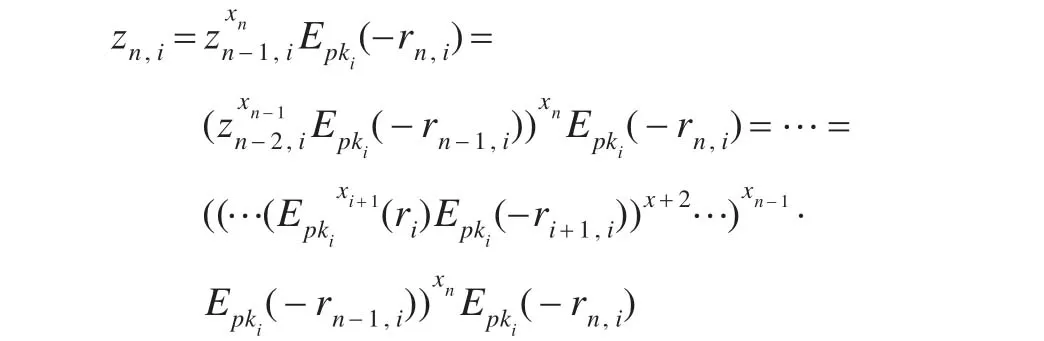
根據2.1節加同態性質，Pi解密zn，i得到：

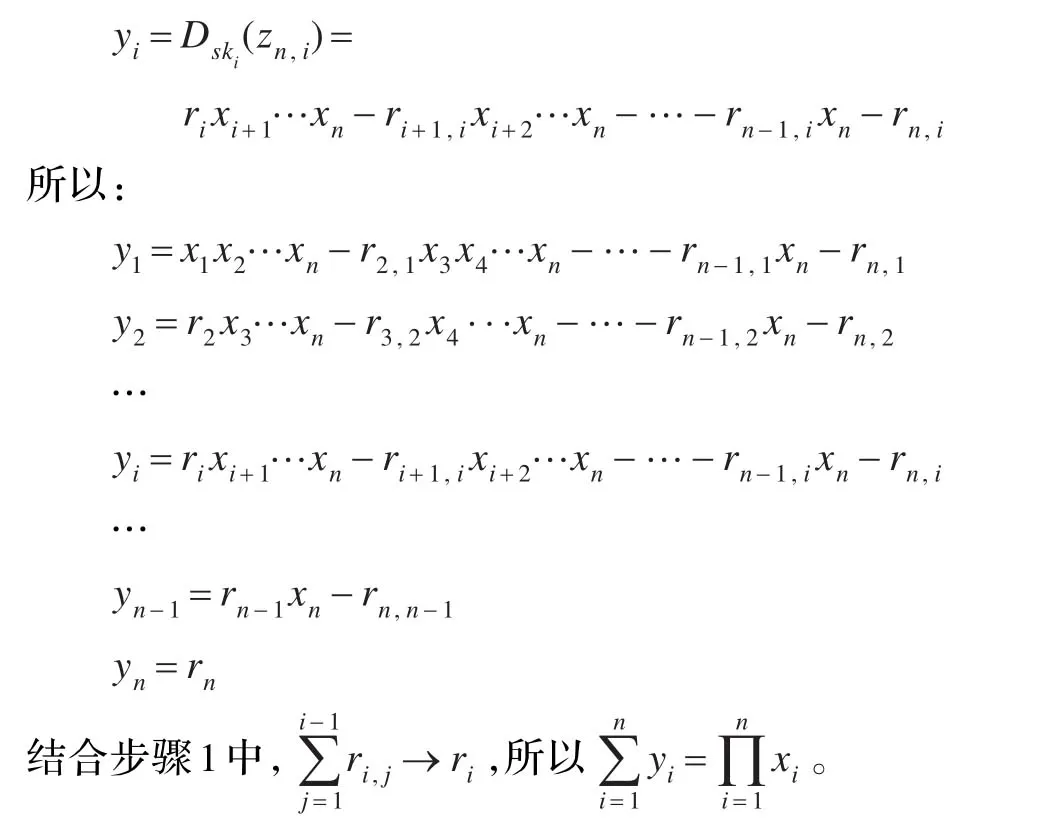
綜上所述，協議1是正確的。

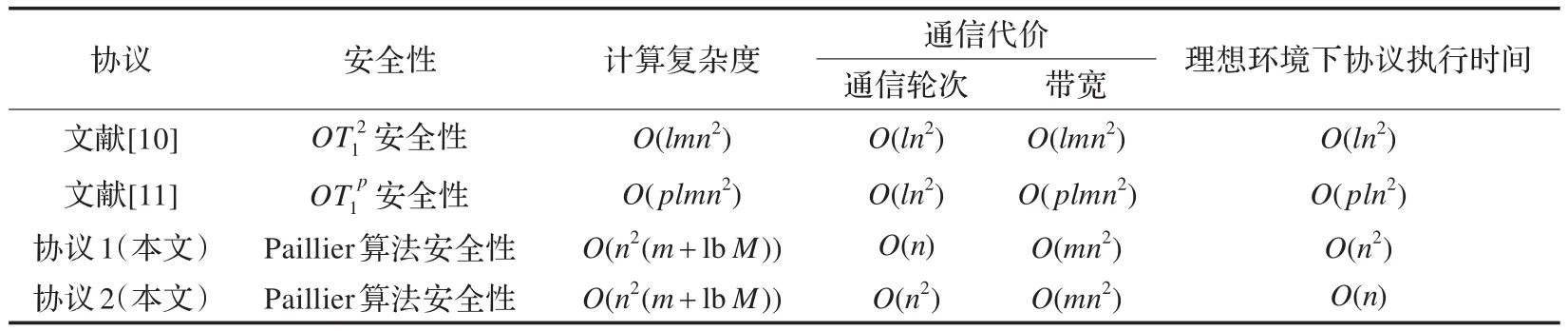
表1 安全多方乘積協議比較

安全性分析：

定理2在半誠實模型下，串行多方乘積協議參與方除了得到yi，無法得到其他參與方秘密。

證明設串行多方乘積協議標記為π，通過構造模擬器的方式對π進行安全性證明：

對Pi(i=1，2，…，n)的視圖：Pi通過協議π在步驟2中得到由Pi-1發送的數據zi-1，1，zi-1，2，…，zi-1，i-1。對Pi產生視圖可記為：

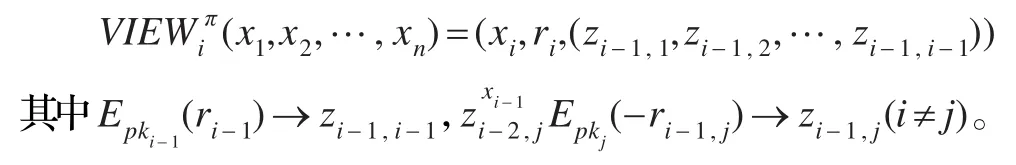
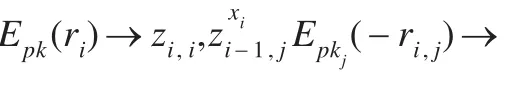
綜上所述，串行多方乘積協議是安全的，參與方除了得到yi，無法得到其他參與方秘密。

效率分析：

（1）計算復雜度。假設本協議的數據長度為mbit，Paillier加密方案的模為M，那么一次加密或者解密需要2lbM次模乘，一次模指運算E(x)k最多2m+1次模乘。步驟2中，Pi加密計算i個中間數據，需要i-1次模指運算和i次加密運算，步驟4中進行一次解密運算。所以總計算復雜度為O(n2(m+lbM))次比特模乘運算。

（2）通信 復雜 度。 由步 驟 2 中 SEND(Pi，Pi+1，zi，1，zi，2， …，zi，i) 和 步 驟 3 中 SEND(Pi，Pi+1，zn，i+1，zn，i+2， …，zn，n)可知，協議1的參與方Pi只與Pi+1進行兩次通信，發送n個數據。所以總的通信輪次是線性的，帶寬O(mn2)。

3.4.2 協議2的性能分析

定理3協議2的正確性、安全性以及計算復雜度同協議1，協議2通信輪次O(n2)，帶寬O(mn2)。

證明 在協議1中，參與方Pi一次計算i個中間數據且等全部計算結束之后發送給Pi+1。而由協議2的執行步驟步驟2可知，Pi每當計算出一個中間數據就立即發送給Pi+1。因此，協議2與協議1僅僅是數據流的不同，數據量以及計算方法沒有發生變化，所以協議2的正確性、安全性以及計算復雜度同協議1。由定理1和定理2可知協議2是安全正確的。

另外，協議2總數據量沒有變化，所以總帶寬為O(mn2)。但每次只實時發送一個數據，因此增加了參與方之間的通信輪次，總通信輪次為O(n2)。

3.4.3 協議比較

本協議與現有安全多方乘積協議的性能比較，如表1所示。表中，l、p為茫然傳輸安全系數，n為參與方個數，m為數據長度。文獻[11]提出多方矩陣乘積協議，當矩陣維數是1的時候就退化為數量乘積。假設在理想通信環境下，計算一個中間數據的時間為1。

由表1可知，本文利用同態加密技術，在保證安全性的同時，減少了數據量，避免了文獻[10]和文獻[11]中所有參與方兩兩之間都需要頻繁通信的情況，降低了通信代價。在計算代價相當的情況下，協議1和協議2各有優勢，串行協議通信輪次少，適用于通信較為復雜的網絡環境；當網絡環境較為理想或者參與方數量較多時，并行協議參與方無須等待，可以減少協議的執行時間。

此外，本文的通信模型為環形，此模型可進一步優化。根據參與方之間的通信代價，設計一個通信代價最低的環，提高協議執行效率；也可以結合信任評估模型[15]設計一個通信方之間信任度最高的環，提高協議的安全性。與文獻[10]和文獻[11]中的復雜網狀模型相比，本文降低了對通信環境的要求，無需所有參與方之間都存在通信關系，只要能形成一個通信環，協議便能正確執行，減少了被攻擊的途徑。

4 結束語

安全多方計算在信息和通信安全中都占有重要的地位，而同態加密技術是安全多方計算中的關鍵技術之一。結合實際，本文提出了兩個適用不同環境的安全多方乘積協議，協議無須第三方的參與，在保證安全性的同時降低了通信代價，提高了協議的執行效率。此外，現有的安全多方計算協議多為兩方協議的擴展，本文提出一個SMC基礎協議，為研究安全多方計算其他問題提供了新思路。本文是基于半誠實模型下的協議，惡意模型下參與方可能不完全遵守協議，如何對參與方的行為進行驗證，構建安全的多方計算協議有待進一步研究。

[1]Yao A C.Protocols for secure computations[C]//Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science.Los Alamitos：IEEE Computer Society Press，1982：160-164.

[2]Goldreich O，Micali S，Wigderson A.How to play any mental game[C]//Proceedings of the 19th Annual ACM Conference on Theory of Computing，1987：218-229.

[3]劉文，羅守山，王永濱.安全兩方向量優勢統計協議及其應用[J].電子學報，2010，38（11）：2573-2577.

[4]秦靜，張振峰，馮登國，等.一個特殊的安全雙方計算協議[J].通信學報，2004，25（11）：35-42.

[5]Du Wenliang.A study of several specific secure two-party computation problems[D].West Lafayette：Purdue University，2001.

[6]肖倩，羅守山，陳萍，等.半誠實模型下安全多方排序問題的研究[J].電子學報，2008，36（4）：709-714.

[7]劉文，王永濱.安全多方信息比較相等協議及其應用[J].電子學報，2012，40（5）：871-876.

[8]Maurer U.Secure multi-party computation made simple[C]//Proceedings of the 3rd International Conference on Security in Communication Networks，2003：14-28.

[9]李禾，王述洋.關于除法的安全兩方計算協議[J].計算機工程與應用，2010，46（6）：86-88.

[10]張華.陳智雄.肖國鎮.一個基于簽密技術的安全多方乘積協議[J].計算機科學，2005，32（2）：50-52.

[11]羅文俊，李祥.多方安全矩陣乘積協議及應用[J].計算機學報，2005，28（7）：1230-1235.

[12]Naor M，Pinkas B.Oblivious transfer with adaptive queries[C]//Advancesin Cryptology（CRYPTO’99）.Berlin Heidelberg：Springer-Verlag，1999.

[13]Paillier P.Public-key cryptosystems based on composite degreeresiduosity classes[C]//Advancesin Cryptology（EUROCRYPT’99）.Berlin Heidelberg：Springer-Verlag，1999：223-238.

[14]Goldreich O.Secure multi-party computation（manuscript Version1.3）[EB/OL].（2009-10-09）[2013-01-18].htttp：//www.wisdom.weizmann.ac.il/～oded/pp.html.

[15]Duma C，Shahmehri N，Caronni G.Dynamic trust metrics for peer-to-peer systems[C]//Proceedings of the 16th International Workshopon DatabaseandExpertSystems Applications.[S.l.]：IEEE，2005：776-781.