基于模糊CMAC的移動機器人軌跡跟蹤控制

金 娟，王耀南

湖南大學 電氣與信息工程學院，長沙 410082

1 引言

近年來對非完整系統的研究得到了國內外學者的普遍關注。作為一類典型的非完整控制系統，移動機器人的鎮定和軌跡跟蹤問題較為復雜，主要是因為受非完整約束的系統不滿足Brockett的光滑鎮定條件，不存在連續時不變的反饋控制律使其鎮定到某一位置[1]。文獻[2-3]采用Lyapunov直接法和積分反演技術對移動機器人的軌跡跟蹤問題進行了研究，對滿足一定條件的參考模型實現了全局指數跟蹤。文獻[4]采用基于CMAC的算法實現了跟蹤，算法簡單但存在抖動。上述方法主要基于非完整移動機器人的運動學模型，要實現完美的軌跡跟蹤控制，需要考慮移動機器人的動力學特性。文獻[5]針對移動機器人的動力學模型，首先利用力矩控制和反演技術結合，設計了軌跡跟蹤的控制律，所得結果具有全局穩定性。文獻[6]將魯棒自適應方法用于移動機器人的力矩控制，設計了全局穩定的軌跡跟蹤控制律，但沒有對存在未知參數和不確定擾動下的系統進行研究。文獻[7]針對存在未知參數和不確定擾動的系統提出了模糊自適應律，但是設計算法復雜。文獻[8-10]在極坐標系下采用滑模控制，在存在外界擾動的情況下也取得了良好的跟蹤效果。本文從移動機器人的運動學和動力學模型出發，利用模糊CMAC神經網絡來逼近系統的非線性和不確定性，同時與速度誤差結合起來構成力矩控制器，并用滑模項來補償不確定性擾動對系統的影響。所設計的控制器結構簡單，算法易于實現，對滿足一定條件的參考軌跡可以實現全局跟蹤，并且對于有界未知擾動具有很強的魯棒性。Lyapunov穩定性定理證明了其穩定性，仿真結果驗證了其有效性。

2 移動機器人模型

圖1所示的移動機器人是一個典型的非完整機械系統，它由兩個同軸安裝的驅動輪和一個輔助前輪組成，兩個驅動輪由兩個直流電機獨立驅動以負責機器人的運動和轉向。兩輪的半徑都為r，輪距為2R，移動機器人的重心位置為C，P為驅動輪連接線的中心，C與P的距離為d。用向量q=[xcycθ]T來表示移動機器人在笛卡爾坐標系中的位置，其中xc，yc表示重心C點在笛卡爾坐標系中的坐標，θ為坐標系{C，XC，YC}與笛卡爾坐標系的夾角。

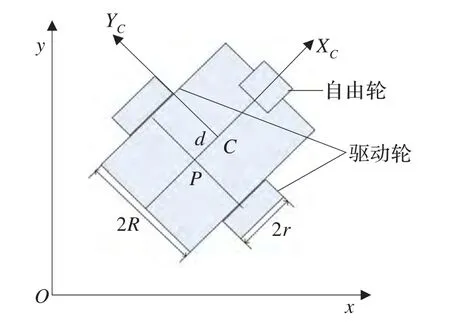
圖1 移動機器人示意圖

一般而言，具有n維系統狀態并受m維約束的非完整移動機器人的動力學方程可以表示為[11]：

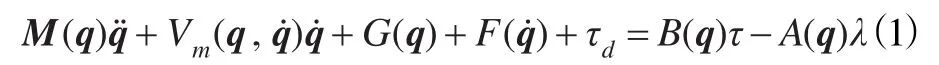
式中，M(q)∈Rn×n為正定對稱慣性矩陣；Vm(q，q˙)∈Rn×n為向心力和哥氏力矩陣；G(q)∈Rn為重力矩陣，F(q˙)∈Rn為摩擦力，對于在光滑平面運動的移動機器人，G(q)和 F(q˙)都為零；τd∈Rn為有界的未知擾動；τ∈Rr為控制輸入向量；B(q)∈Rn×r為輸入變換矩陣；λ∈Rm為約束力；A(q)∈Rn×m為約束矩陣。

非完整約束可以表示為：

選擇一個n-m維的滿秩矩陣S(q)為 AT(q)零空間的一組基，即有：

從式（2）和（3）中可以得到一個輔助的速度控制輸入量 v(t)∈Rn-m，有：

對于圖1所示的移動機器人，非完整約束使其只能在與驅動輪輪軸垂直的方向上運動，即必須滿足純滾動和無滑動的條件：

因此，式（1）中的約束矩陣可以表示成：

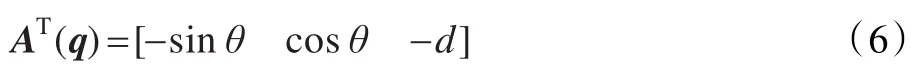
進而S(q)可表示成：

那么，式（4）所表示的運動學方程為：

其中，v(t)=[vω]T，v和ω分別表示移動機器人的線速度和角速度。

由Euler-Lagrange方程可得圖1所示移動機器人模型的動力學參數[8]：

其中，m表示移動機器人的質量，I表示轉動慣量，τr和τl分別表示左右輪的力矩。

將式（1）左乘ST(q)并化簡可得：

由文獻[11]可知式（10）的參數矩陣有如下性質：

性質1對于任意的q，慣性矩陣(q)是正定的。

性質2矩陣函數是斜對稱的，即對于任意向量α，有：

在此假設移動機器人的有界未知擾動滿足||-τd||≤dB。根據（9）可得（10）的參數矩陣為：

3 模糊CMAC

小腦神經關節控制器（CMAC）[12]是一種基于神經生物學的、簡單快速的神經網絡，能夠學習任意多維非線性映射。與BP神經網絡一類的全局逼近方法相比，CMAC有很多優點，它具有局部逼近能力、連續輸入輸出能力和一定的泛化能力，結構簡單，學習速度快，特別適合于實時控制。但是傳統的CMAC也有自身的不足，由于輸入狀態與聯想強度之間的關系只是簡單的“激活”和“不激活”的關系，不符合人腦認識事物的模糊性和連續性，導致CMAC的自適應性較差。文獻[13-15]將模糊理論引入CMAC，對CMAC的輸入空間劃分方式和聯想單元激活方式進行模糊化處理，使得輸入空間劃分方式以及聯想強度的激活活性可在線調整，從而提高了控制器的自學習能力。其仿真結果表明模糊CMAC具有更好的自適應性和魯棒性。本文不再對模糊CMAC的優越性進行仿真比較說明，而是直接將其用于對移動機器人動力學模型不確定參數的逼近。

模糊CMAC的具體模型如圖2所示。根據后文的需要，在此以逼近4輸入2輸出的函數為例進行說明。

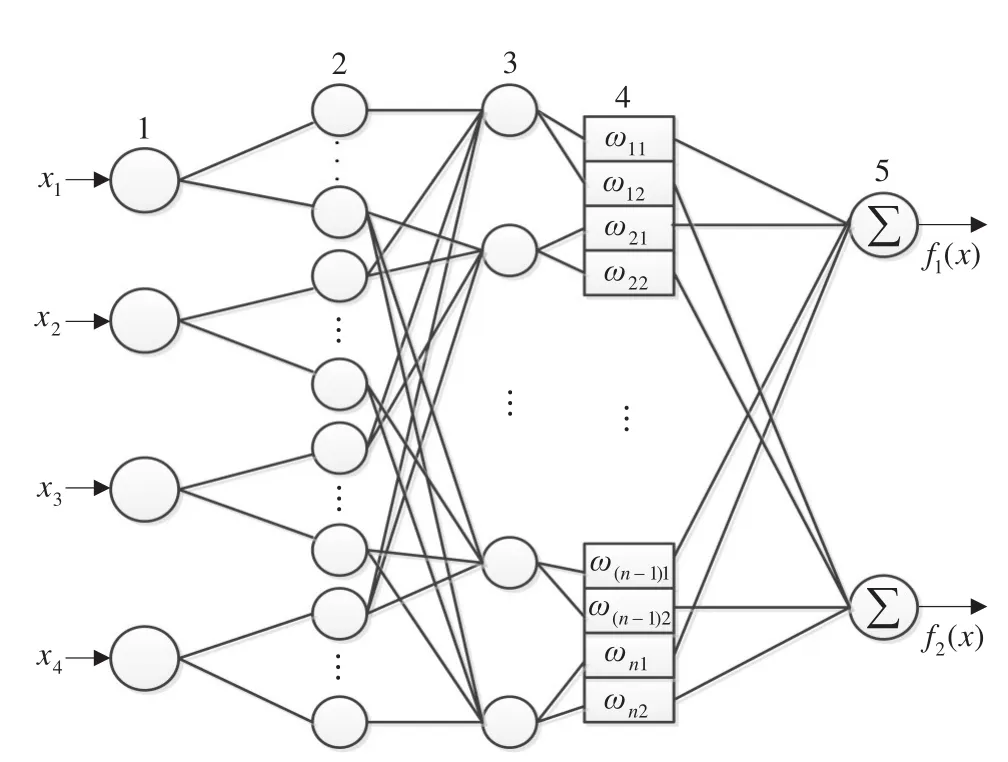
圖2 模糊CMAC結構圖

第一層為輸入層：

第二層為模糊化層，本文采用高斯基隸屬函數對輸入進行模糊化處理。

假設所有輸入xi是連續有界的，在每個輸入xi的論域上定義n個“塊”Bij，輸入xi對“塊”Bij的隸屬關系為：

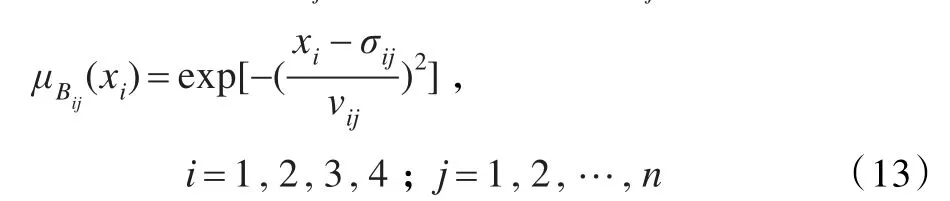
式中，σij表示函數的中心值，vij表示函數的寬度。則第二層的輸入與輸出的關系為：

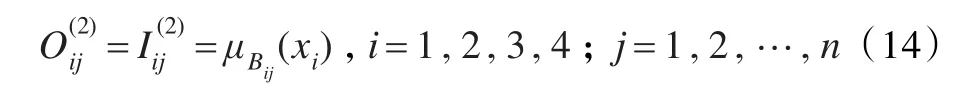
第三層為模糊相連層，用于得出對聯想單元的激活強度。所有輸入論域對應的塊組成n4個超立方體Hq，每個超立方體與一個聯想單元對應，每個聯想單元則存儲相應的聯想強度。激活強度相當于xi對于各個塊的隸屬度的“與”，本文用乘法實現“與”操作，有：

第四層以第三層求出的激活強度激活聯想單元的聯想強度，各個聯想單元輸入輸出關系為：

其中ωqi表示各個聯想單元的聯想強度。

第五層為輸出層，對聯想單元進行求和以恢復系統信息：

通過將ωqi寫成矩陣的形式，有：

4 控制器設計和穩定性分析

4.1 控制器設計

下面從移動機器人的運動學和動力學模型出發，設計軌跡跟蹤控制器。控制系統的結構如圖3所示。

用qr=[xryrθr]T表示參考軌跡，q=[xy θ]T表示移動機器人的實際運動軌跡，則在局部坐標系下的跟蹤誤差可以表示為ep=T(qr-q)，即

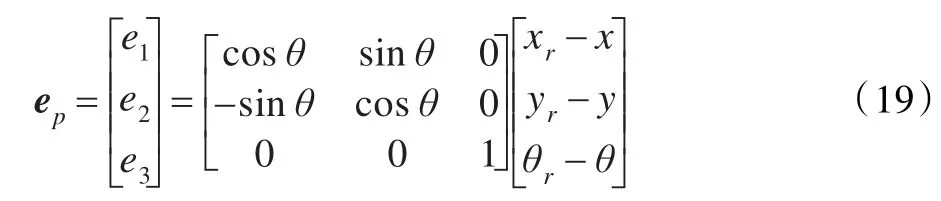
那么，誤差變化率為：

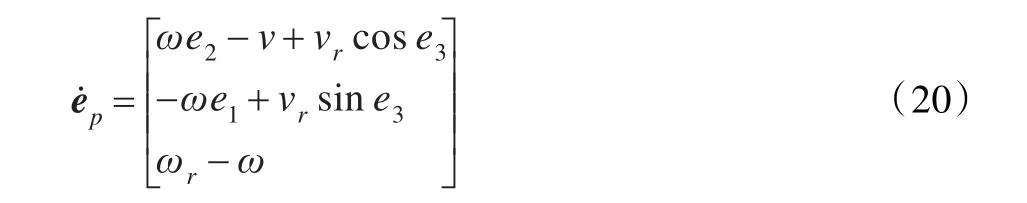
文獻[2]給出在給定速度vr＞0的前提下，跟蹤運動學模型（8）的速度控制輸入為：

其中，k1，k2，k3＞0 為設計參數。

對于參考速度vc，定義速度跟蹤誤差為ec，令ec=[e3,e4]T=vc-v，對該式求導并結合（10），可得速度跟蹤誤差下的動力學方程：

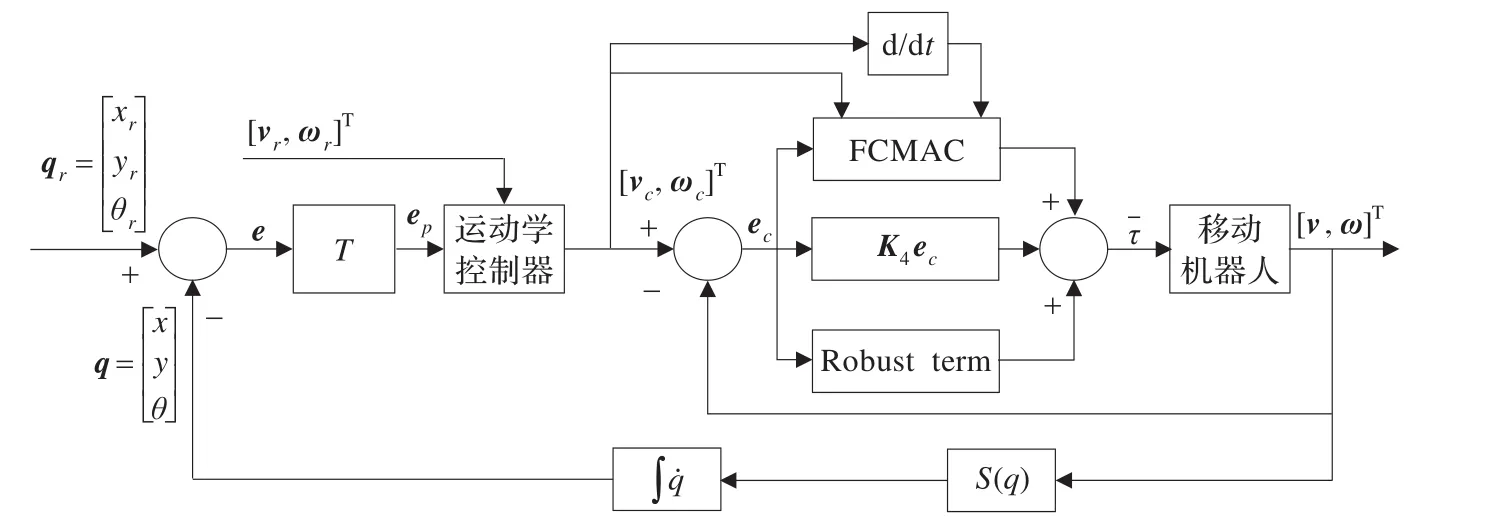
圖3 基于模糊CMAC的控制結構圖

那么通過計算力矩法來進行跟蹤控制的合適的控制輸入可選為：

K4ec為負反饋項，且K4為正定的對角增益矩陣；γ用于補償系統中未建模的不確定性擾動。

將此控制用于式（22），則速度跟蹤誤差動力學模型變為：

其中：

其中，Kd為正定對角矩陣，其值依賴于擾動的大小，需滿足 min(diag(Kd))≥dB。

4.2 穩定性分析和權值更新算法

選取Lyapunov函數如下：

其中

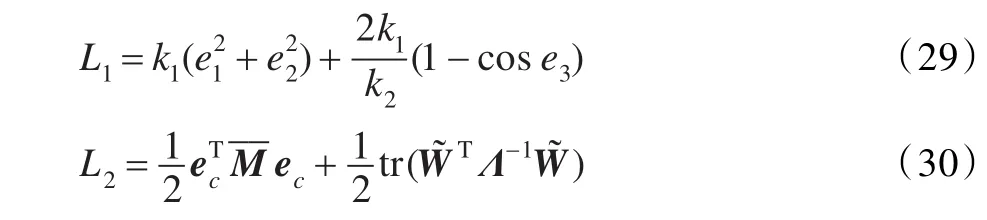
顯然，L≥0，只有在ep，ec，都為零時，有L=0。

對式（29）求導，有：

將式（20）、（21）代入上式中，得：

因為給定線速度vr＞0，所以L˙≤0。

對式（30）求導，有：

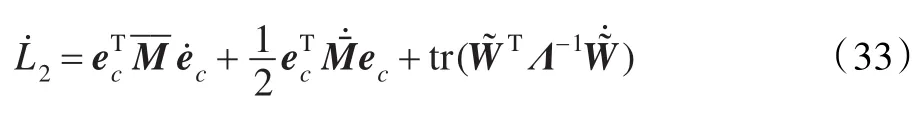
代入速度誤差模型式（26）得：

其中K4min、Kdmin分別為 K4和Kd的最小奇異值。

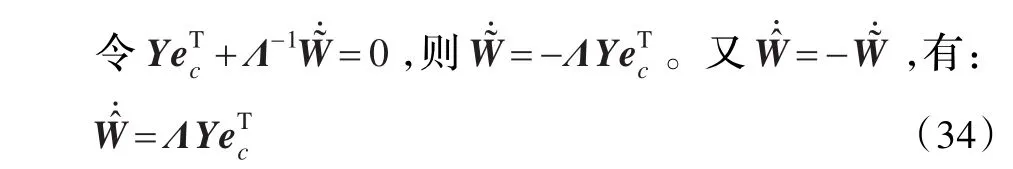
進而可簡化為：

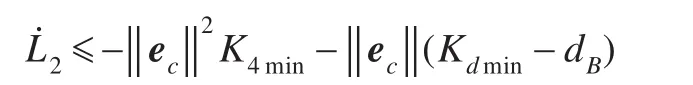
由于 min(diag(Kd))≥dB，有≤0 ，定理得證。

式（34）為模糊CMAC的權值更新學習算法，該算法簡單易于實現。

5 仿真結果及分析

為了驗證所設計方法的有效性，本文以圖1所示的兩輪差分驅動的非完整移動機器人為控制對象進行matlab仿真實驗，其中，m=10 kg，I=5 kg·m2，2R=0.4 m ，r=0.05 m ，d=0。

設參考軌跡為x2+y2=r2，r=2，其中參考線速度為vr=0.2 m/s，參考角速度為ωr=0.1 rad/s。參考機器人和實際機器人的初始位置分別為qr(0)=[2 0pi/2]T和q(0)=[1 . 7 0pi/2]T。控制器的參數選為k1=1，k2=2，k3=2，K4=15I2，Λ=0.7I2，Ik為k×k的單位矩陣。仿真時設=[2cos(5t);2sin(5t)]，并選取正定矩陣 Kd為[2.5，0；0，2.5]。

仿真結果如圖4和圖5所示，圖4為系統沒有加擾動的跟蹤情況，圖5為加擾動后的跟蹤情況。在兩組圖中，圖（a）實線所示為移動機器人的參考軌跡曲線，虛線為實際跟蹤曲線，圖（b）xe所示為x軸方向的跟蹤誤差，ye所示為y軸方向的跟蹤誤差，thetae表示方向誤差。由仿真結果可知，移動機器人能實現對給定曲線快速且平穩的跟蹤，并且位姿誤差也能快速收斂到零。通過對比有無擾動的情形可知，設計的控制器對有界不確定性擾動具有很強的魯棒性。

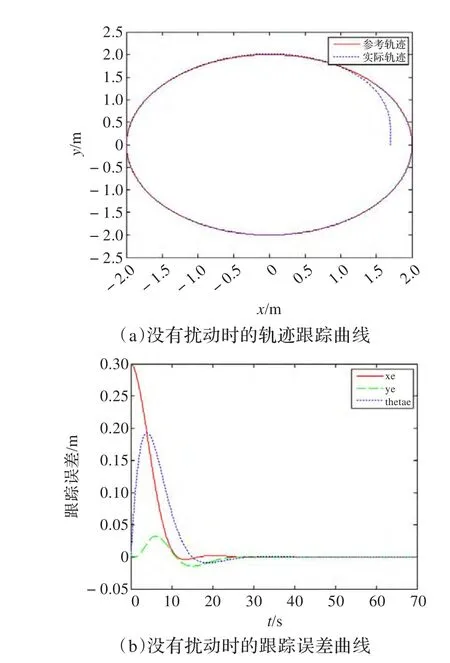
圖4 沒有擾動時的軌跡跟蹤曲線與跟蹤誤差曲線

圖5 有擾動時的軌跡跟蹤曲線與跟蹤誤差曲線

6 結論

本文從移動機器人的運動學和動力學模型出發，提出了基于模糊CMAC的跟蹤控制器，該控制器能夠很好的消除移動機器人的動態不確定性和擾動對系統的影響，Lyapunov穩定性定理保證了系統的穩定性和跟蹤誤差的漸近收斂。仿真結果表明了該控制器的有效性和魯棒性。

[1]Komannovsky H，Macclamroch N H.Developments in nonholonomic control systems[J].IEEE Control systems magazine，1995，15（6）：20-36.

[2]Jiang Z P，Nijmeijer H.Tracking control of mobile robots：A case study in backstepping[J].Automatica，1997，33（7）：1393-1399.

[3]吳衛國，陳輝堂，王月娟.移動機器人的全局軌跡跟蹤控制[J].自動化學報，2001，27（3）：326-331.

[4]Li Xin，Chen Wei，Chen Mei.Application of CMAC-based algorithm of critics&strategists on robot tracking control[C]//Proceedings of the International Conference on Networking and Digital Society，2010：298-302.

[5]Fierro R，Lewis F L.Control of a nonholonomic mobile robot：backstepping kinematicsinto dynamics[J].Journal of Robotic Systems，1997，14（3）：149-163.

[6]Chang Y，Chen B.Adaptive tracking control design of nonholonomic mechanical systems[C]//Proceeding of the 35th Conference on Decision and Control，1996：4739-4744.

[7]Tamoghna D，Indra N K.Design and implementation of adaptive fuzzy logic-based controller for wheeled mobile robots[J].IEEE Transactions on Control Systems Technology，2006，14（3）：501-510.

[8]Yang J，Kim J.Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots[J].IEEE Transactions on Robotics and Automation，1999，15（3）：578-587.

[9]Chwa D.Sliding-mode tracking control of nonholonomic wheeled mobile robots in polar coordinates[J].IEEE Transactions on Control Systems Technology，2004，12（4）：637-643.

[10]Park B S，Yoo S J.Adaptive neural sliding mode control of nonholonomicwheeledmobilerobotswithmodel uncertainty[J].IEEE Transactions on Control Systems Technology，2009，17（1）：207-214.

[11]Fierro R，Lewis F L.Control of a nonholonomic mobile robot using neural network[J].IEEE Transactions on Neural Networks，1998，9（4）：589-600.

[12]王耀南.機器人智能控制工程[M].北京：科學出版社，2004：83-109.

[13]王源，胡壽松.基于自組織模糊CMAC網絡的非線性系統魯棒自適應跟蹤控制[J].自動化學報，2002，28（6）：984-989.

[14]孫煒，王耀南.模糊CMAC及其在機器人軌跡跟蹤控制中的應用[J].控制理論與應用，2006，23（1）：38-42.

[15]Shieh H L，Bao Chin Y.A robust fuzzy CMAC for function approximation[C]//Proceeding of the9th International Conference on Machine Learning and Cybernetics，Qingdao，China，11-14 July，2010：2962-2966.