一類向量似變分不等式問題
張 娟,薛建明
(昆明理工大學津橋學院工學系,云南昆明650106)
近些年,凸的概念已經從很多角度得到了推廣和延伸[1-3]。Karamardian等于1990年證明了函數的廣義凸與它們的梯度函數的單調性是等價的,并指出廣義單調在變分不等式問題中的作用與目標函數的廣義凸性在數學規劃中的作用是相同的。
Ali Farajzadeh等[4]在可度量化的拓撲向量空間中建立了向量似變分不等式問題與向量優化問題之間的等價性,但其中所涉及的函數都是偽-invex的。YANG X M等[5]在空間Rn中給出了函數的廣義凸與它們的梯度函數的廣義單調之間的一系列關系。
文中在可度量化的拓撲向量空間中給出了Univexity,偽 -univexity及擬 -univexity等一類比invex函數更廣的函數的概念,并在偽-univexity的假設下得到了類似文獻[4]中的結果。
1 預備知識
設X是一可度量化的拓撲向量空間。記X上的度量為d,其中d滿足條件:d(x+z,y+z)=d(x,y),d(tx,0)=td(x,0),?x,y,z∈ X,t > 0。
定義 1[4]稱函數 f:X→ R在 x∈ X附近是M-Lipschitz,若存在一常數 M > 0,使得
|f(y)- f(z)|≤ Md(y,z),
其中,y,z為x的某一鄰域的任意點。稱函數f:X→R在X上是局部Lipschitz的,若它在X的每一點附近都是Lipschitz的。
定義2[4]如果函數 f:X→ R在 x∈ X附近是Lipschitz的,則函數f在x∈X沿著方向v∈X的Clarke廣義導數定義如下:
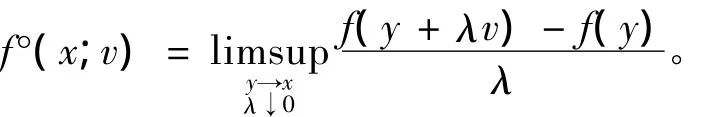
定義3[4]函數f:X→R在x∈X的Clarke廣義梯度定義如下:
?f(x)={ξ∈ X*:〈ξ,v〉≤ f°(x;v),?v∈ X}。因此,對?v∈X
f°(x;v)=max{〈ξ,v〉:ξ∈ ?f(x)}。這些定義和性質可以被推廣到局部Lipschitz的向量值函數f:X→Rp。記fi(i=1,…,p)為f的分量,則f在x∈X點的Clarke廣義梯度是集合
?f(x)=?f1(x)× ?f2(x)× … × ?fp(x)。
下面給出文獻[5-8]中Univexity以及單調性的推廣。
定義4 設X0是X的一非空子集。稱X0在u關于η:X0×X0→X是invex的,若對任意x∈X及λ∈[0,1],有 u+ λη(x,u)∈ X0。
稱X0關于η:X0×X0→X是invex的,若X0在每一點都是invex的。
定義5 稱非光滑函數f:X0?X→R
1)關于η,φ及k是univex的,若存在函數η:X0×X0→X,φ:R→R及k:X0×X0→R+,使得
k(y,x)φ[f(y)- f(x)]≥〈ξ,η(y,x)〉,?x,y ∈ X0,?ξ∈ ?f(x);
2)關于η,φ及k是嚴格univex的,若存在函數η:X0×X0→X,φ:R→R及k:X0×X0→R+,使得
k(y,x)φ[f(y)- f(x)] > 〈ξ,η(y,x)〉,?x,y ∈ X0,x ≠ y,?ξ∈ ?f(x);
3)關于η,φ及k是 (嚴格)偽-univex的,若存在函數η:X0×X0→X,φ:R→R及k:X0×X0→R+,使得
k(y,x)φ[f(y)- f(x)](≤)< 0?〈ξ,η(y,x)〉< 0,?x,y∈ X0,?ξ∈ ?f(x);
4)關于η,φ及k是擬-univex的,若存在函數η:X0×X0→X,φ:R→R及k:X0×X0→R+,使得
k(y,x)φ[f(y)- f(x)]≤ 0?〈ξ,η(y,x)〉≤ 0,?x,y∈ X0,?ξ∈ ?f(x);
5)關于η,φ及k是強偽-univex的,若存在函數η:X0×X0→X,φ:R→R,k:X0×X0→R+及常數α >0,使得
〈ξ,η(y,x)〉≥0?k(y,x)φ[f(y)- f(x)]≥α‖η(y,x)‖,?x,y∈ X0,?ξ∈ ?f(x)。
例1[8]Univex函數是比invex函數更廣的一類函數,如:
設 f(y)=y3,?y∈ R,φ(a)=3a,?a ∈ R,
則f是 univex的,但不是 invex的[4]。這是因為對y= - 3,x=1,f(y)- f(x)< ▽f(x)η(y,x)。
例2[8]偽-Univex函數是比Univex函數更廣的一類函數,如:
則f是偽-univex的,但不是univex的。這是因為對
▽f(x)η(y,x)> k(y,x)φ[f(y)- f(x)]。
條件A[7]設η:X0× X0→X,則對?x,y∈X0及 λ ∈[0,1],
η(y,y+ λη(x,y))= - λη(x,y),η(x,y+ λη(x,y))=(1 - λ)η(x,y)。
顯然,由條件A知,有
η(y+ λη(x,y),y)= λη(x,y)。
定義6 設X0是X中關于η:X0×X0→X的invex集。稱集值映射F:X0→2X0在X0上關于η是(嚴格)偽 -invex單調的,若
〈F(x),η(y,x)〉≥0?〈F(y),η(y,x)〉(>)≥0,
?x,y ∈ X0,x ≠ y。
定義7 設X0是X中關于η:X0×X0→X的invex集。稱集值映射 F:X0→2X0在 X0上關于 η是擬-invex單調的,若
〈F(x),η(y,x)〉> 0?〈F(y),η(y,x)〉≥0,?x,y ∈ X0,x ≠ y。
定義8 設X0是X中關于η:X0×X0→X的invex集。稱集值映射F:X0→2X0在X0上關于η是強偽-invex單調的,若存在一常數β>0,使得
〈F(x),η(y,x)〉≥ 0?〈F(y),η(y,x)〉≥β‖η(y,x)‖,?x,y ∈ X0,x ≠ y。
2 非光滑univex函數的刻畫
將文獻[9]中得到的結果推廣至可度量化的拓撲向量空間中的非光滑的情形。假設X0是X中的非空invex集。定理1 假設
1)X0是X中關于η的開invex集;
2)η滿足條件A;
4)集值映射 ?f在 X0上關于 η,φ 及 k是偽-invex單調的,
則f在X0上關于η,φ及k是偽-univex的。證 設 x,y∈ X0,x≠ y使得
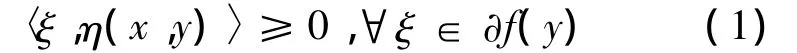
下證 k(x,y)φ[f(x)- f(y)]≥0。
假設上述不等式不成立,即
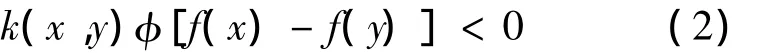
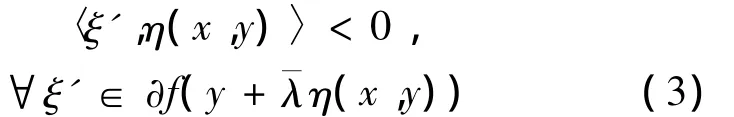
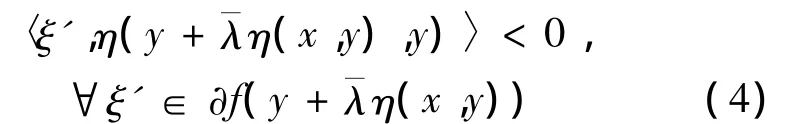
因為?f在X0上關于η是偽-invex單調的,由式(4)得,對某一∈(0,1),有
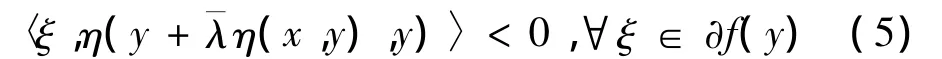
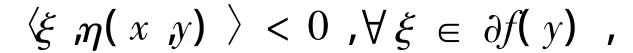
這與式(1)矛盾。因此,f在 X0上關于 η,φ及是偽-univex的。定理2 假設
1)X0是X中關于η的開invex集;
2)η滿足條件A;
4)集值映射?f在X0上關于η,φ及k是嚴格偽-invex單調的,則f在X0上關于η,φ及k是嚴格偽 -univex 的。
證 結合嚴格偽-univex的定義及條件1)~4),按照定理1的方法即可證得定理2成立。
定理3 假設
1)X0是X中關于η的開invex集;
2)η滿足條件A;
4)集值映射 ?f在 X0上關于 η,φ 及 k是擬-invex單調的,則 f在 X0上關于 η,φ及 k是擬 -univex 的。
證 假設f在X0上關于η,φ及k不是擬-univex的,則存在 x,y ∈ X0,使得
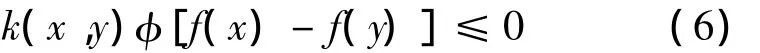
但
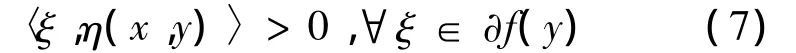
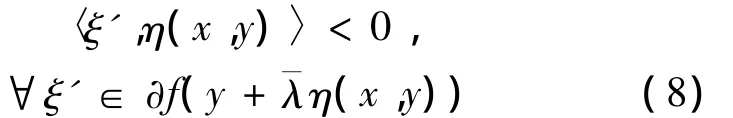
由條件A,有
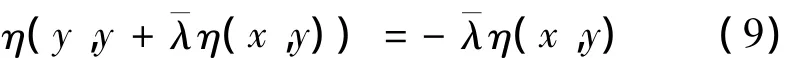
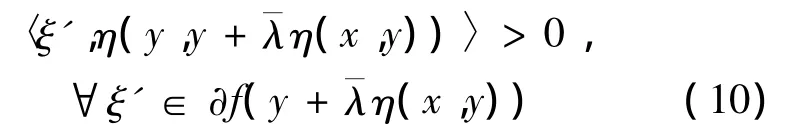
因為集值映射?f在X0上關于η,φ及k是擬-invex單調的,由(10),有
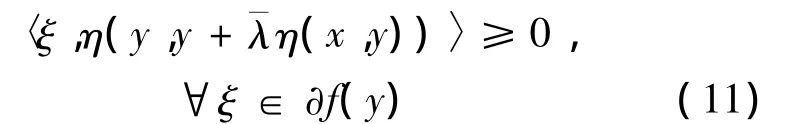
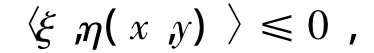
這與式(7)矛盾。因此,f在 X0上關于η,φ及k是擬 -univex 的。定理4 假設
1)X0是X中關于η的開invex集;
2)η滿足條件A;
4)集值映射 ?f在 X0上關于 η,φ 及 k是強偽-invex單調的,則 f在 X0上關于 η,φ及k是強偽-univex的。
證 設 x,y∈ X0,使得
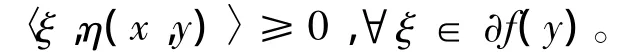
由條件A及假設1),有
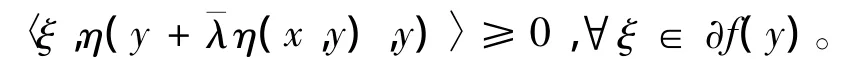
由集值映射?f在X0上關于η,φ及k是強偽-invex單調的,存在常數β>0,使得
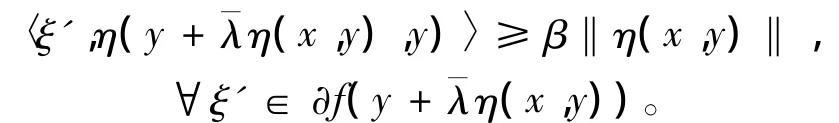
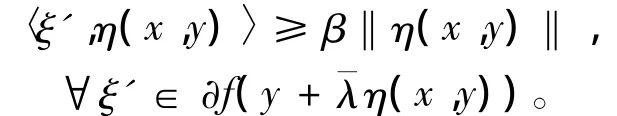
再由假設3)及k(x,y)>0,有
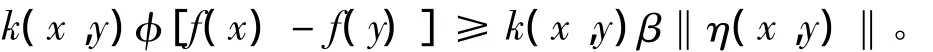
因此,f在X0上關于η,φ及k是強偽-univex的。
3 向量似變分不等式與向量優化問題的關系
考慮如下向量優化問題:
(NVOP)Minimize f(x)=(f1(x),…,fp(x))Subject to x∈X0,
其中fi:X0→R,i=1,…,p為非光滑局部Lipshcitz函數。
同時,考慮下面的似變分不等式問題:(GVVLIP)非光滑向量似變分不等式問題就是找到一個點y∈X0,且對?ξ∈?f(y),不存在x∈X0,使得〈ξ,η(x,y)〉≤0。(GWVVLIP)非光滑弱向量似變分不等式問題就是找到一個點 y∈ X0,且對 ?ξ∈ ?f(y),不存在x∈X0,使得〈ξ,η(x,y)〉< 0。
在非光滑univextiy的假設下,文中將推廣文獻[4]中的結果。定理5 假設
1)X0是X中的非空invex集;
2)f在X0上關于η,φ及k是非光滑univex的;
3)φ(a)≤0,當且僅當a≤0;
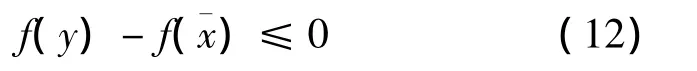
由式(12)及假設3),有
k(y,x)φ[fi(y)-fi()]≤0,i=1,…,p。又f關于η,φ及k是非光滑univex的,因此存在y∈X0,使得
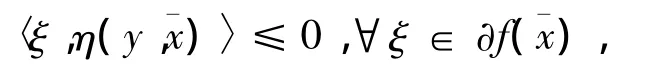
定理6 假設
1)X0是X中的非空invex集;
2)-f在X0上關于η,φ及k是嚴格-univex的;
3)φ(a)<0,當且僅當a<0;
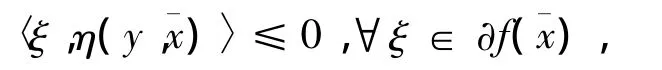
由 -f在X0上關于η,φ及k是嚴格-univex的,有
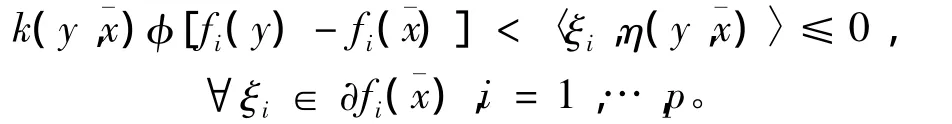
又由式12)有
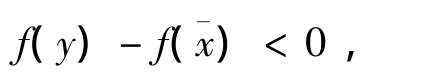
這與假設(4)矛盾。
由于(NVOP)的每一個有效解都是其弱有效解,因此由定理6有如下結論:推論1 假設
1)X0是X中的非空invex集;
2)-f在X0上關于η,φ及k是嚴格-univex的;
3)φ(a)<0,當且僅當a<0;
1)X0是X中的非空invex集;
反之,若
3)f在X0上關于η,φ及k,是嚴格偽-univex的;
4)φ(a)≤0,當且僅當a≤0;
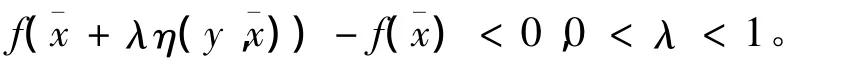

因此,不存在y∈X0,使得

再由假設4),有
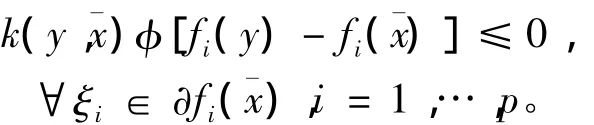
又f=(f1,…,fp)在 X0上關于 η,φ 及 k是嚴格偽-univex的,因此存在y∈X0,使得
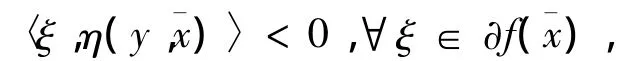
定理8 假設
1)X0是X中的非空invex集;
2)f在 X0上關于 η,φ及 k是非光滑嚴格偽 -univex 的;
3)φ(a)≤0,當且僅當a≤0;
定理9 假設
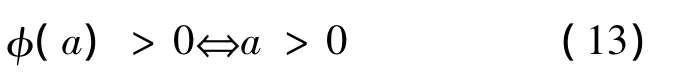
則所有的臨界點都是有效解,當且僅當f在X0上是嚴格偽-univex的。
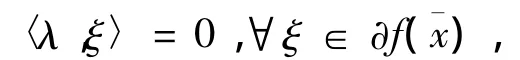
因此,
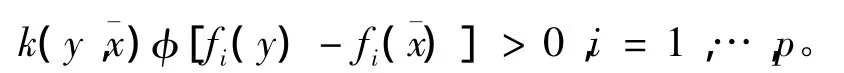
又由式(13),有
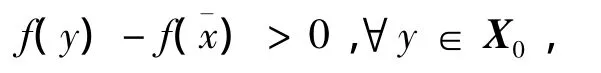
即不存在y∈X0,使得
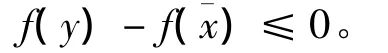
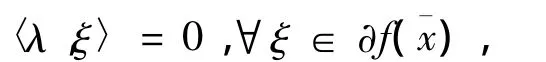
因此,
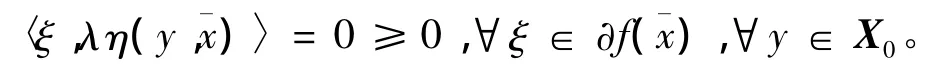
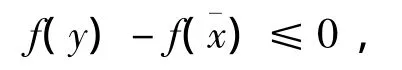
再由式(13)知,不存在y∈X0,使得
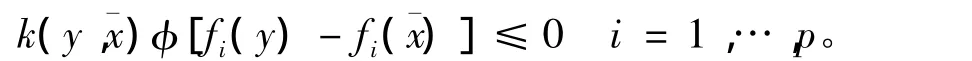
因此,f在X0上是嚴格偽-univex的。推論2 假設
1)X0是X中的非空invex集。
2)f在X0上關于η,φ及k是嚴格偽-univex的;
3)φ(a)<0,當且僅當a <0;φ(a)≥0,當且僅當a≥0。
[1]Hanson M A.On suficiency of the Kuhn-Tucker conditions[J].JMath Anal Appl,1981,80(2):545-550.
[2]Ruiz-Garzoon G,Osuna-Goomez R,Rufian-Lizana A.Generalized invex monotonicity[J].European Journal of Operational Research,2003,144(3):501-512.
[3]FAN Liya.Generalized invexity of nonsmooth functions[J].Nonlinear Analysis,2008,69(11):4190-4198.
[4]Ali Farajzadeh,Muhammad Aslam Noor,Khalida Inayat Noor.Vector nonsmooth variational-like inequalities and optimization problem[J].Nonlinear Anal,2009,71(7/8):3471-3476.
[5]YANG X M,Teo K L,YANG X Q.Higher-order generalized convexity and duality in non-differentiable multi-objective mathematical programming[J].JMath Anal Appl,2004,297(1):48-55.
[6]Mohan SR,Neogy SK.On invex sets and preinvex functions[J].JMath Anal Appl,1995,189(3):901-908.
[7]Weir T,Mond B.Pre-invex functions inmultiple objective optimization[J].JMath Anal Appl,1988,136(1):29-38.
[8]Mishra Shashi Kant,WANG Shouyang,LAIKin Keung.Generalized Convexity and Vector Optimization[M].Berlin Heidelberg:Springer-Verlag,2009.
[9]FAN Liya,LIU Sanyang,GAO Shuping.Generalized monotonicity and generalized convexity of nondifferentiable functions[J].J Math Anal Appl,2003,279(1):276-289.

