MQ函數和M atern函數在LM APS方法中的比較

楊海婷， 張學瑩

(河海大學理學院，江蘇 南京210098)

近年來，無網格方法在計算偏微分方程數值解方面發展迅速，當遇到網格劃分困難、網格突變以及網格移動等問題時，無網格方法具有明顯的優勢。

全局配點型 RBFs方法［1－2］是一種真正意義上的無網格方法，它成功地克服了上述困難，但是采用它求解偏微分方程時隨著插值節點數的增加，系數矩陣的條件數增大，容易導致系數陣奇異，滿秩甚至病態，這給處理大規模的問題帶來不便。為了改進這些問題，文獻［3－5］采用局部徑向基函數節點插值法減少了矩陣的病態性。之后，CHEN C S等人采用LMQ思想，在近似特別解(Method of Approximate Particular Solution，MAPS)［6］的基礎上提出了局部近似特別解法(簡稱 LMAPS)［7］。LMAPS方法具有MAPS和RBFs的優點，它不僅規避了全局矩陣的病態和滿秩，而且可以用較少的節點數獲得更高的精度。目前，LMAPS方法已經取得了很大的發展并廣泛應用于物理領域。

文中介紹了MQ函數中形參c的優化方法，分別選取MQ函數和Matern函數作為LMAPS方法中的徑向基函數，并將這兩種函數應用到規則區域和不規則區域上的偏微分方程進行數值求解，同時給出相應的誤差比較分析。

1 LMAPS方法的基本理論

1.1 控制方程

考慮偏微分方程

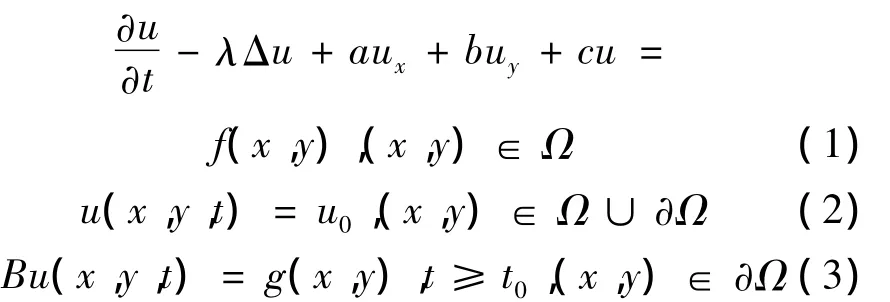
其中，λ，a，b，c是給定的常數，Δ是二階線性Laplace算子，B 是邊界算子，f(x，y)，g(x，y)和 u0是給定的函數。

1.2 LM APS方法的基本理論

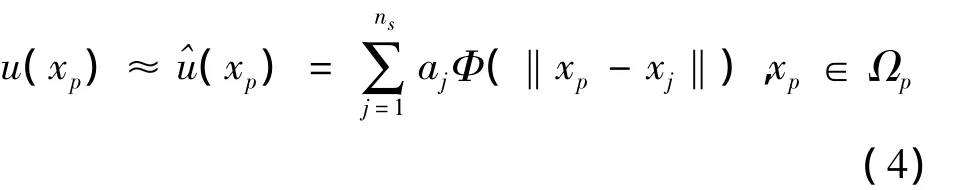
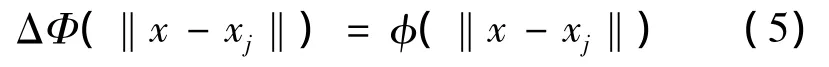
這里‖·‖是歐幾里得范數，φ是徑向基函數。

此處

并且

由于局部支撐域內各插值節點相異，從而矩陣Φns可逆，故有

對于?xp∈Ω，將方程(1)在空間上離散得到

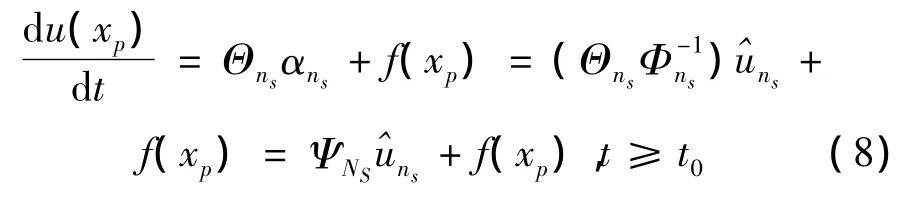
其中

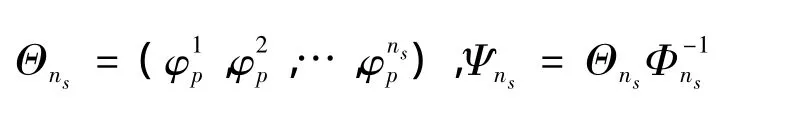
并且

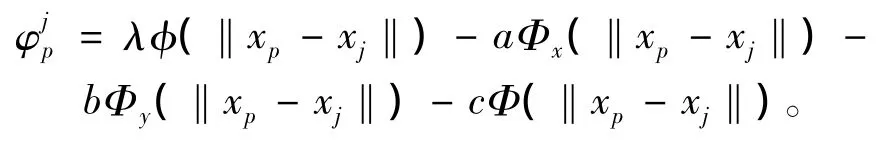
通過在適當位置添加零元素將向量Ψns延拓成n維向量 Ψn［7］，則有

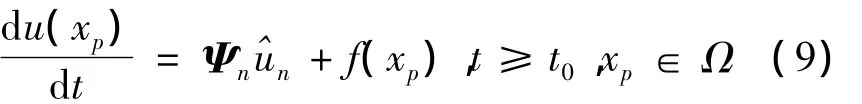
1.3 MQ函數和M atern函數

局部近似特別解方法是一種基于RBFs的無網格方法，用它求解偏微分方程得到的數值解的精度很大程度上取決于基函數。MQ函數具有收斂速度快、插值精度高的特點，而相比MQ函數，Matern函數插值的LMAPS方法則省去了調節形參c的時間，在降低計算量的基礎上提高了計算效率。文中選取MQ函數和Matern函數作為LMAPS方法中的基函數，并根據數值結果進行誤差比較分析。這里采用MQ函數的一般形式:

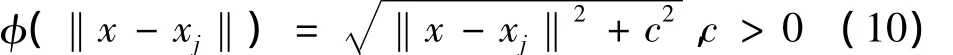
其中，x=(x，y)表示在物理空間上支撐域內點的坐標，c是形狀參數，對方程(5)求積分［8-9］可得

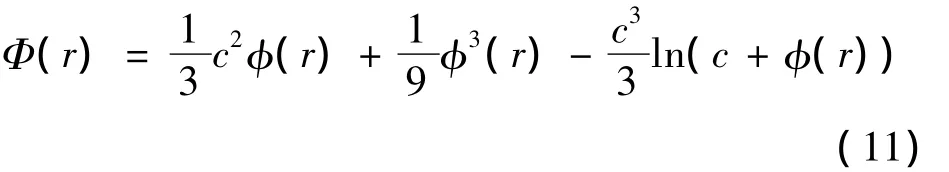
其中，r= ‖x－xj‖。

如果選取Matern函數作為基函數有

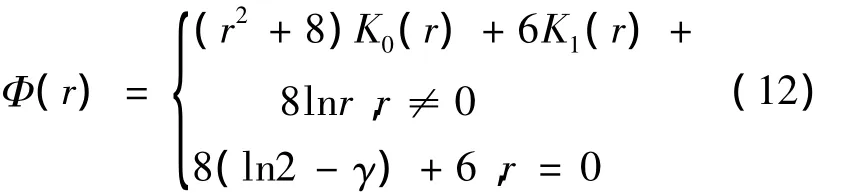
其中，ΔΦ =r2K2(r)，γ是歐拉常數，K0(r)和K1(r)分別是0階和1階第二類貝塞爾函數。

1.4 形參c的優化方法

由于形參c的選取直接影響基于MQ函數插值的LMAPS方法的近似精度，傳統意義下，通過不斷嘗試不同的形參c［10］或者一些特殊的方法，比如說，Contour Pade’算法［11］來規避系數陣的病態或滿秩從而得到一個合適的形參。但是這些方法都增加了計算成本，降低了計算效率并且給處理大規模問題帶來諸多不便。

為了尋找最優形參c，并且平衡用MQ函數作為基函數的LMAPS方法求解PDEs得到的數值解的精確性和穩定性，這里采用以分析交叉驗證(Leave－One－Out Cross Validation，LOOCV)［12］方法為理論基礎的Rippa LOOCV算法來解決離散數據插值問題中形參c的優化以及局部支撐域內ns的選取問題［12-13］。

2 數值算例

為了比較MQ函數和Matern函數在LMAPS方法中的近似精度，采用基于這兩種函數的LMAPS方法求解不規則區域和規則區域上的偏微分方程，并給出誤差分析。求解過程中選取kd－tree算法進行局部區域相鄰節點的搜索，并分別通過Rippa LOOCV算法以及不斷調試形參c來提高計算的近似精度和計算效率。最大絕對誤差(MAE)、最大相對誤差(MRE)、均方根誤差(RMSE)定義如下:

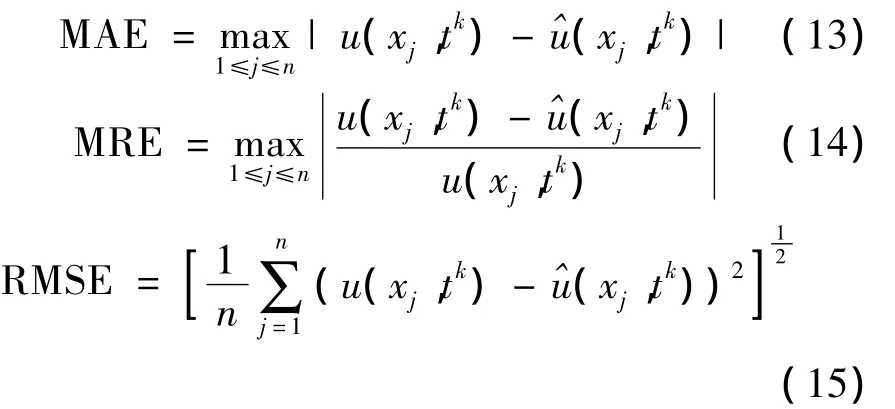
其中，n是總節點數，k是時間層，^u(xj，tk)和 u(xj，tk)分別表示k時間層上的數值解和精確解。

這里選取常見于靜電學、機械工程等物理領域的Possion方程以及被用來解決激波、淺水波、交通流動力學等物理問題的Burgers′方程作為數值算例來驗證上述兩種函數的有效性。

算例1 考慮不規則區域下不規則點分布的二維Possion方程其邊界是一個不規則區域，計算區域如圖1所示。

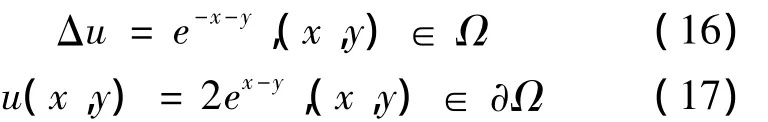
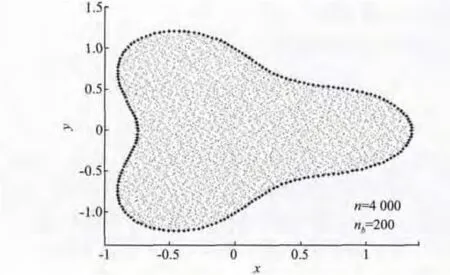
圖1 n=4 000，nb=200時不規則區域下節點不均勻分布的Possion問題的計算區域Fig.1 Computational domain and distribution of the interior and boundary points with n=4 000，nb=200

圖2 是總節點數n=4 000，邊界點數nb=200時，優化形參c后的MQ函數和Matern函數作為基函數得到的相對誤差對比圖。可以看出，這兩種函數的計算精度都比較滿意，在整個不規則計算區域上得到的誤差基本一致，并且都是平滑下降的。相比MQ函數，Matern函數在不規則邊界各角處的誤差出現了輕微的波動現象。

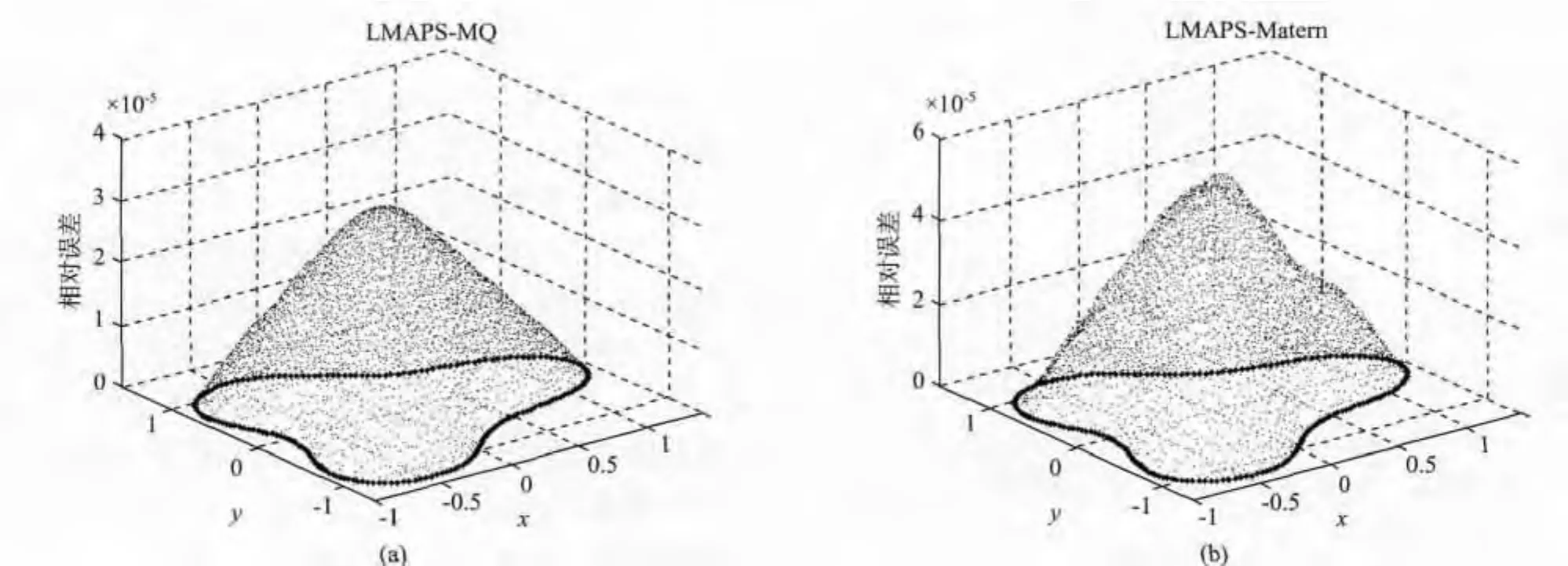
圖2 n=4 000，nb=200時MQ和Matern函數得到的相對誤差比較Fig.2 Profile of RAE using MQ and Matern with n=4 000，nb=200

表1為nb=200，n不同時，MQ和Matern函數得到的誤差結果。一般而言，n越多，網格劃分越密，所得的數值解精度越高，但實際并非如此。與MQ函數相反，隨著n的增大，Matern函數取得的誤差不斷增大，當增大到某個特定值時，MQ函數得到的誤差產生了較大的波動并出現了增大趨勢。這說明誤差不僅與總節點數目n有關，還與節點分布有著密切的關系。

總的來說，在處理不規則點不均勻分布問題時，優化形參c后的MQ函數得到的數值結果相比LMAPS－Matern方法具有更高的計算精度和計算效率。但是在總節點數n增大到一定程度條件下，此時從數值解的穩定性上來看，Matern函數相比MQ函數更有優勢。

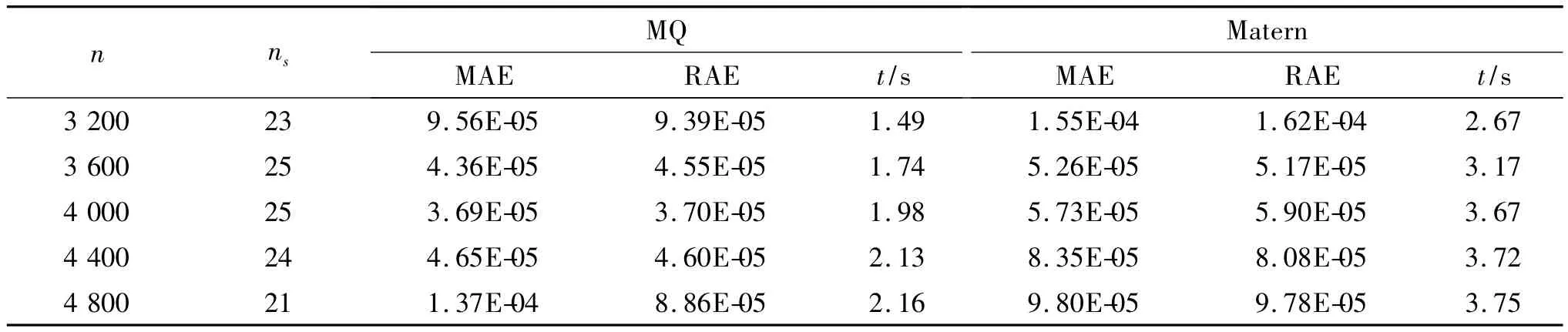
表1 MQ和Matern函數在不同n時數值結果的誤差對比Tab.1 Errors and com putational time versus nusing MQ and Matern

算例2 考慮二維不定常Burgers′方程組:

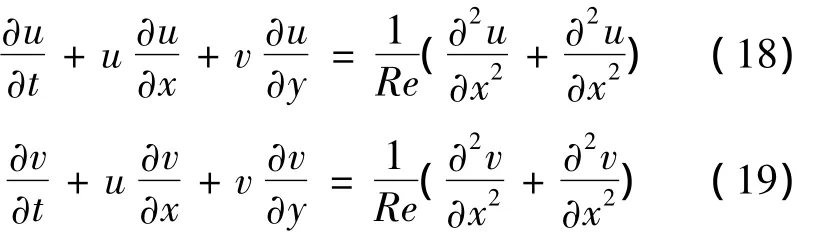
其中，Ω ∪ ?Ω = ［0，1］2，0 ＜ t＜ + ∞，方程的精確解［14］ 為

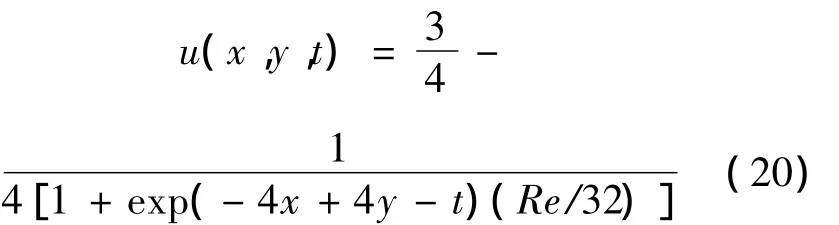
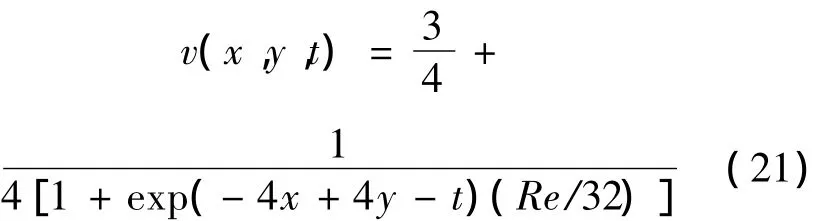
圖3，4 是在 n=441，Re=100，Δt=10－3的條件下，t分別取t=0，t=1，t=2時的數值解圖像。由圖可見，MQ函數和Matern函數求得的數值結果基本一致，隨著時間的增大，數值解的梯度變大，解的不連續性增強。此外，與v相反，得到的u的數值解的不連續區域在時間t的推動下逐漸向坐標中心移動。

圖3 n=441，Re=100，c=50時MQ函數在不同時刻得到的數值結果Fig.3 uand v distributions obtained by MQ with n=441，Re=100，c=50 at different time

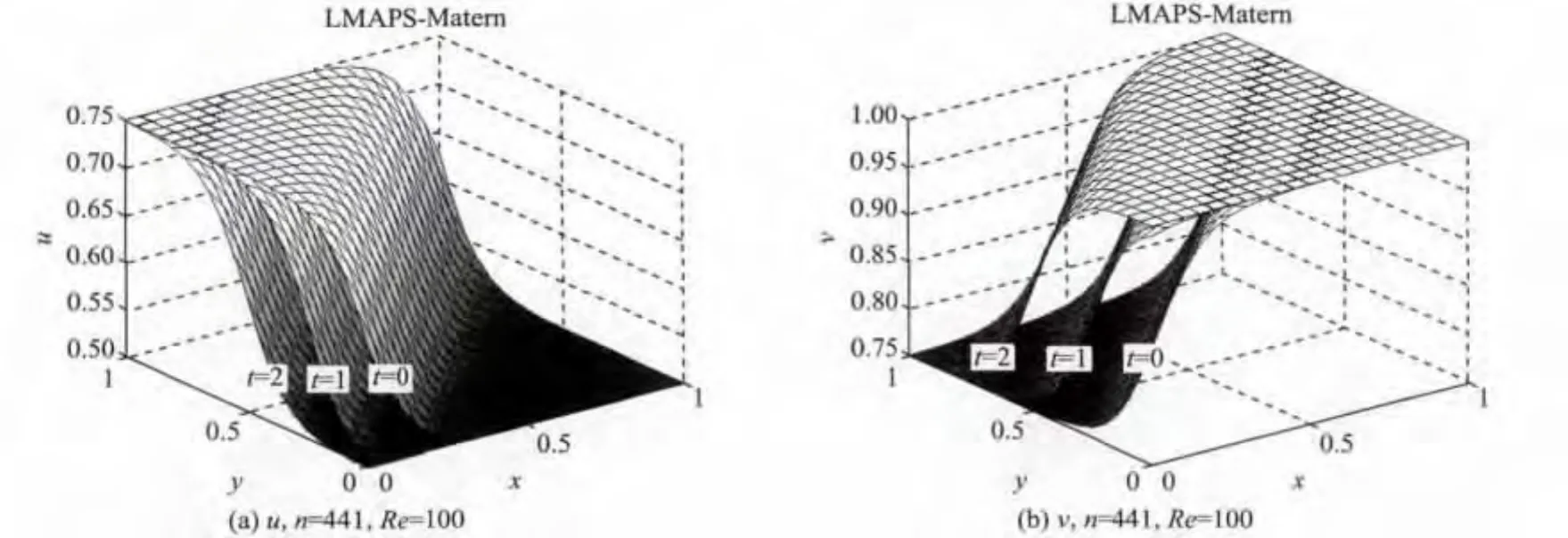
圖4 n=441，Re=100時M atern函數在不同時刻得到的數值結果Fig.4 uand v distributions obtained by Matern with n=441，Re=100 at different time

表 2，3 是 Δt=10－4，t=0.1 時，兩種函數得到的誤差。數值結果表明它們都達到了相似的近似精度，并且隨著Re的增大，誤差均明顯增大，當Re增大到某一特定值時，相比MQ函數，Matern函數得到了更精確的結果。同時隨著總節點數的不斷增多， Matern函數的優勢也更加明顯。

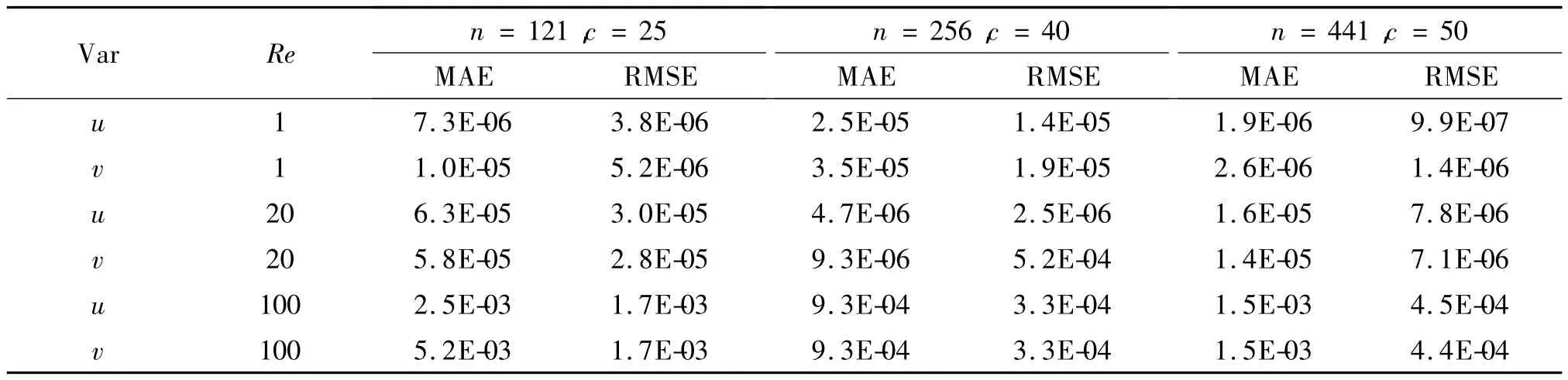
表2 t=0.1時MQ函數的誤差結果Tab.2 Obtained error by MQ for example 2 at t=0.1

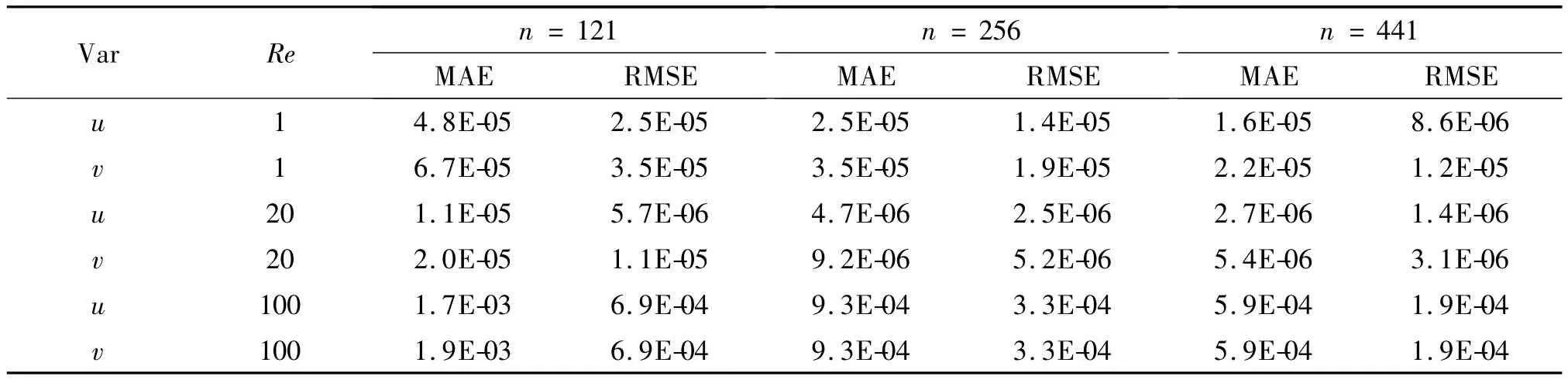
表3 t=0.1時Matern函數的誤差結果Tab.3 Obtained error by Matern for example 2 at t=0.1

結合圖3，4，在圖5中可以看出，隨著Re的增大，在數值解梯度較大的區域，這兩種函數取得的絕對誤差相比光滑的區域要大得多，并且誤差圖像出現了不同層次的波動。當Re達到100時，Burgers′方程接近半雙曲型，此時用這兩種函數作為徑向基函數的LMAPS方法都不能得到穩定的數值解;但是相比MQ函數，Matern函數得到了較高的精度以及較小的波動。總的來說，無論從近似精度還是計算效率上來看，Matern函數對于求解規則區域上多個變量的半雙曲型偏微分方程更有優勢。

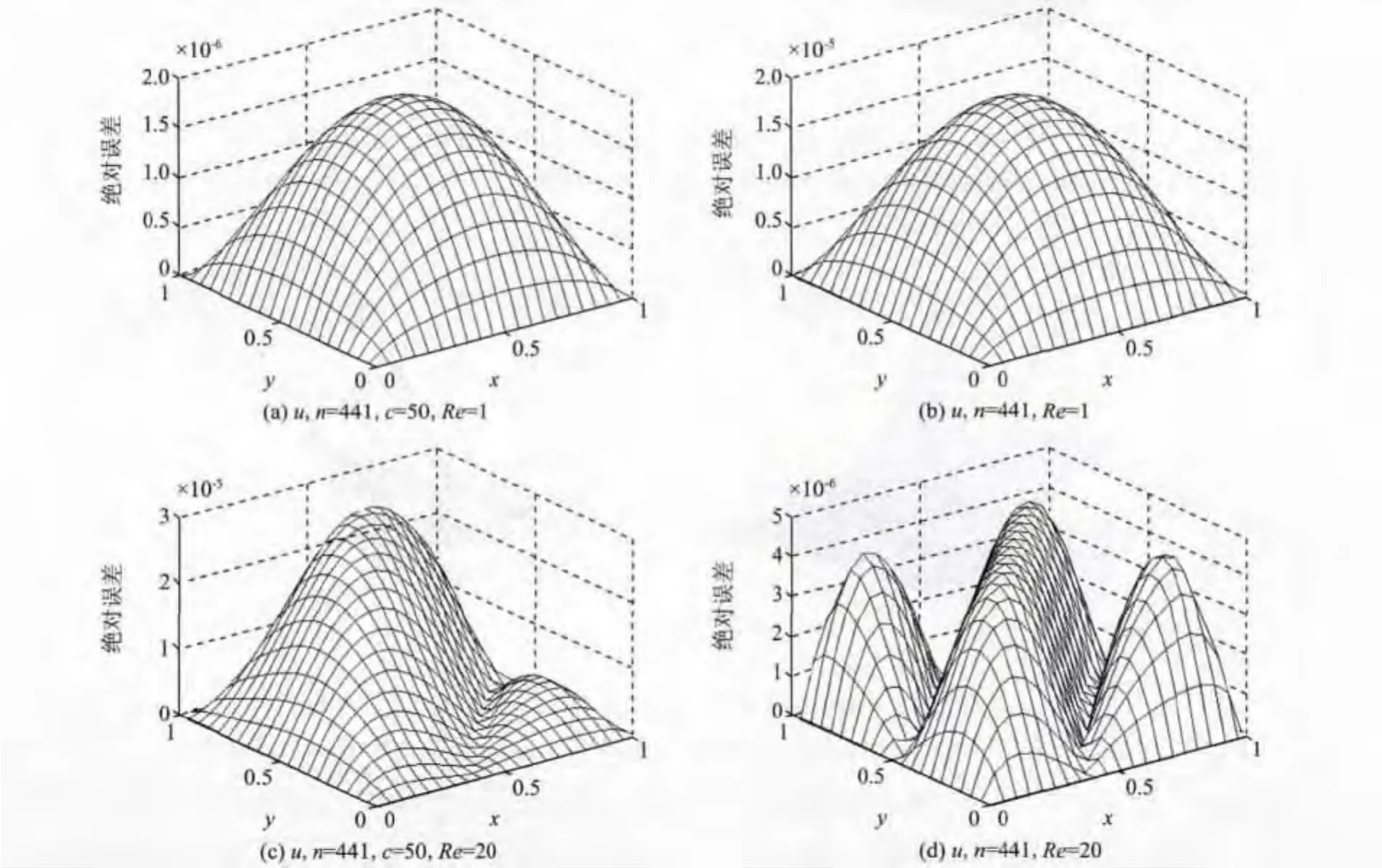
圖5 n=441，t=0.2時MQ和M atern函數在不同下的絕對誤差比較Fig.5 Comparison of the error p rofiles of uobtained by MQ and Matern with n=441，t=0.2

3 結語

介紹了基于徑向基函數插值的無網格LMAPS方法，分別選取MQ函數和Matern函數作為基函數，并利用局部配點法構造低階線性方程組進行插值近似來避免全局矩陣的病態和滿秩。文中選取不規則區域上的Possion問題，采用優化形參c后MQ函數與Matern函數進行誤差比較，同時選取規則區域上的二維Burgers′方程作為算例，并給出相應的誤差分析。

數值實驗表明這兩種函數都取得了較高的精度，由于避免了形參c的選取，優化形參c后MQ函數相比Matern函數得到更高的近似精度和計算效率。而無論是求解不規則區域點不均勻分布問題還是高維半雙曲型的偏微分方程，Matern函數得到的數值解都有著更強的穩定性。

［1］Kansa E J.Multiquadrics－a scattered data approximation scheme with applications to comutational fluid－dynamics.I.surface approximations and partial derivative estimates［J］.Comput Math Appl，1990，19:127－145.

［2］Kansa E J.Multiquadrics－a scattered data approximation scheme with applications to comutational fluid－dynamics.II.solutions to parabolic，hyperbolic and elliptic partial differential equations［J］.Comput Math Appl，2000，39:123－137.

［3］Wendland H.Piecewise polynomial，positive definite and compactly supported radial basis functions ofminimal degree［J］.Adv Comput Math，1995，4(1):389－396.

［4］WU Z.Multivariate compactly supported positive definite radial functions［J］.Adv ComputMath，1995，4(1):283－292.

［5］Vertnik R，Sarler B.Meshless local radial basis function collocation method for convective－diffusive solid－liquid phase change problems［J］.International Journal of Numerical Methods for Heat and Fluid Flow，2006，16:617－640.

［6］CHEN C S，FAN C M，WEN P H.The method of particular solutions for solving certain partial differential equations［J］.Numerical Methods of Partial Differential Equations，2012，28:506－522.

［7］YAO GM，CHEN CS，Kolibal J.A localized approach for themethod of approximate particular solutions［J］.ComputMath Appl，2011，61:2376－2387.

［8］SHU C，DING H，Yeo K S.Local radial basis function－based differential quadrature method and its application to solve twodimensional incompressible Navier－Stokes equations［J］.Computer Methods in Applied Mechanics and Engineering，2003，192:941－954.

［9］CHEN C S，FAN CM，WEN PH.Themethod of particular solutions for solving elliptic problems with variable coefficients［J］.International Journal of Computational Methods，2011，8:545－559.

［10］Kansa E J，Carlson R E.Improved accuracy of multiquadric interpolation using variable shape parameters［J］.Comput Math Appl，1992，24:99－120.

［11］Bengrt F，WrightG.Stable computation ofmultiquadric interpolants for all values of the shape parameter［J］.ComputMath Appl，2004，47:497－523.

［12］Rippa S.An algorithm for selecting a good value for the parameter c in radial basis function interpolation［J］.Adv ComputMath，1999，11:193－210.

［13］Bengrt F，Julia Z.The Runge phenomenon and spatially variable shape parameters in RBF interpolation［J］.ComputMath Appl，2007，54:379－398.

［14］Young D L，FAN C M，HU S P，et al.The Eulerian－Lagrangian method of fundamental solutions for two－dimensional unsteady Burgers equations［J］.Engineering Analysiswith Boundary Element，2008，32:395－412.

(責任編輯:楊 勇)