基于D-H參數法的二自由度并聯機械手逆運動學求解

于豐博，楊惠忠，卿兆波

YU Feng-bo, YANG Hui-zhong, QING Zhao-bo

（中國計量學院 機電工程學院，杭州 310018）

0 引言

在食品、電子和醫藥等輕工業領域，需要機械手對輕小物料進行中、短距離的搬運、分揀、上下料等操作[1～3]。與串聯機構相比，其重負荷比小，且具有精度高、剛度大、承載能力強等特點，故被廣泛應用于高速操作場合[4]。天津大學Diamond機械手在醫藥、飲料包裝中的成功運用充分體現了并聯機械手的高速、可靠優勢[5]。運動位置模型的快速、準確建立對機器人的定位精度控制及其產業化開發至關重要。因此，如何根據企業的不同需求，在最短時間內快速正確建立機械手運動模型具有重要的現實意義。

對二自由度的并聯平動機械手——Diamond機構，由于其機械結構簡單，國內學者多采用幾何法建立運動學求解模型[1～2，5～6]，但隨著機械手自由度的增加，機構幾何約束關系越復雜，求解難度也隨之增大。而通過D-H參數法建立的機械手運動學逆解模型，具有很好的適用性，且求解簡單快捷，并通過MATLAB編程驗證模型的正確性。

1 系統描述及運動學求解

1.1 系統描述

如圖1所示，并聯機器人由兩條支鏈（分別各有一個電機驅動）和動平臺組成，各支鏈包含兩個平行四邊形機構（分別由機架-主動臂-支架-連架副主動臂；支架-從動臂-動平臺組成）[1,7]。

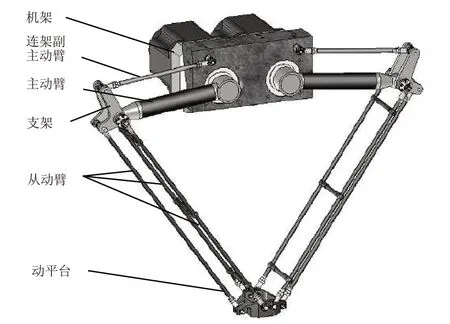
圖1 并聯機器人

圖2 為機器人中去除虛約束后的機構簡圖，即平面五連桿機構，P為末端位置點，l0、l1、l2分別為機架的半長、主動臂長度、從動臂長度。

1.2 連桿坐標系的建立及連桿參數的確定

在圖2機架中間及兩桿各關節處，根據John J. Craig對連桿坐標系建立的約定，確定了機械手的連桿坐標系[8～11]，如圖3所示。

基準坐標系{x0o0y0}建立在機架的中心位置；

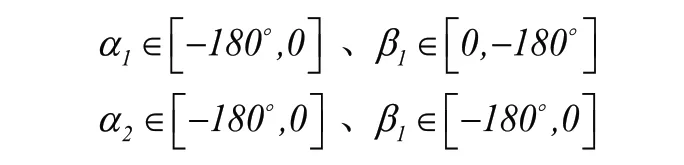
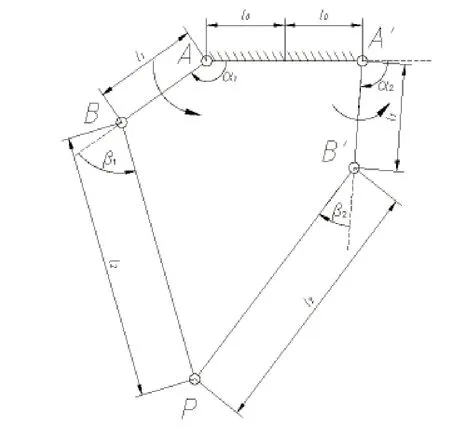
圖2 并聯機器人控制機構簡圖

符號遵從右手法則；oij代表支鏈i（1, 左支鏈；2, 右支鏈）中第j（1 , 2關節序號）關節處坐標系原點。

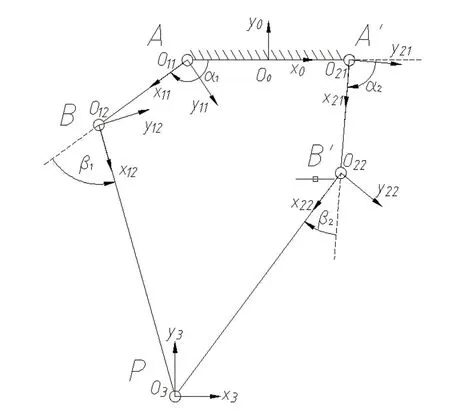
圖3 機械手各連桿坐標系

在對每根連桿建立坐標系的基礎上由Craig法則得到各連桿參數，該規定如下[8,9]：

得到的左、右兩支鏈各連桿參數分別如表1、表2所示。

表2 右支鏈連桿參數表

1.3 模型求解

將坐標系{i}經過旋轉、平移使其與{i-1}重合，則{i}在{i-1}中的位姿描述（即{i}到{i-1}的坐標變換矩陣）為[8～10]：

式中c 代表cos( )，s 代表sin( )，以后均采用這種方法表示。

1）左支鏈末端位置求解

將表1中參數代入式(1)求得各變換矩陣：

從而得到各連桿坐標系對基坐標系的變換矩陣：

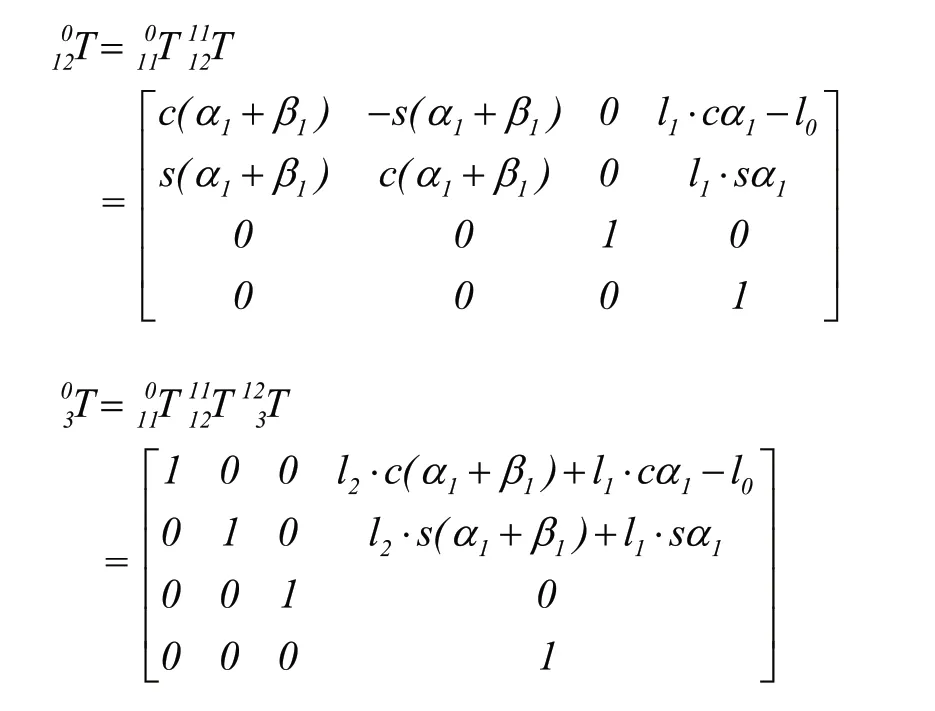
末端點P在基坐標系中的方位描述為：

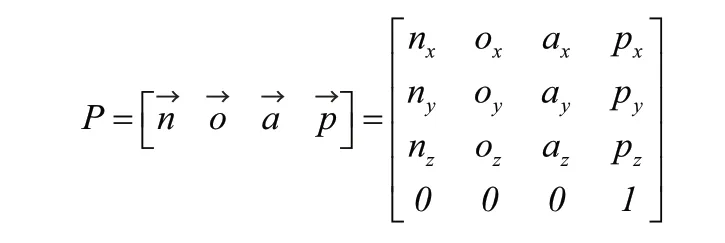
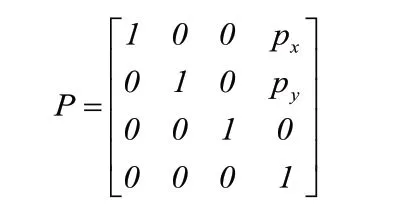
利用末端在基坐標系中的位姿矩陣與末端在工具坐標系（{x3o3y3}）中位姿經坐標系變換之后在基坐標中的描述應該相等建立求解方程的基礎：

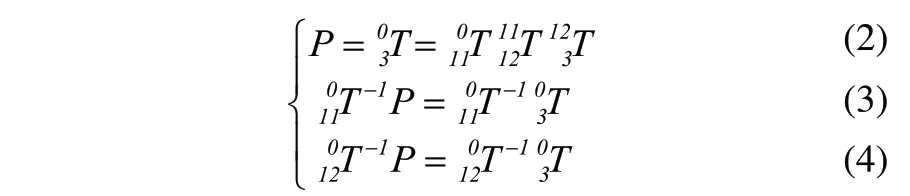
令式(2)等號兩端的（1,4）元素相等，式(3)等號兩端的（2,4）元素相等，式(4)等號兩端的（1,4）、（2,4）元素分別相等建立方程組，同時將各方程中

取非零及在取值范圍內的解，即：

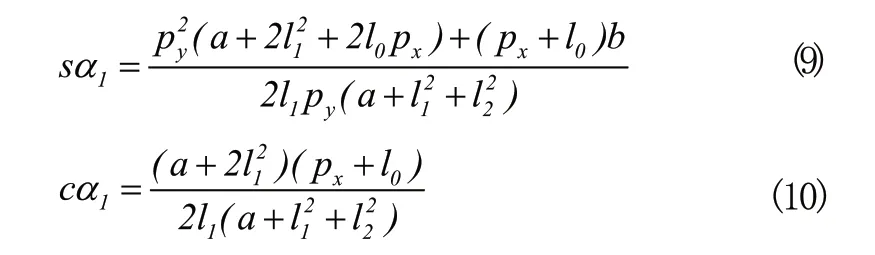
其中：

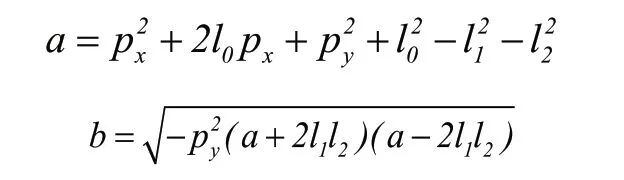
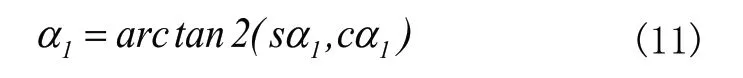
2）右支鏈末端位置求解

右支鏈主動臂轉角的求解過程與左支鏈雷同，此處不再贅述，最終求得：

2 模型驗證

圖4 末端運動軌跡

將圖4中末端運動軌跡中特殊點坐標值及各連桿長度代入式(11)、式(14)，求得轉角與作圖法獲得準確轉角對比分別如圖5中（1,1）、（2,1）（圖5中呈矩陣排列的圖）所示，特殊軌跡點相關參數分別如表3、表4所示；將軌跡特殊點處各關節轉角及連桿長度代入式(2)等號右邊矩陣（1,4）、（2,4）元素中，求得末端點在基坐標系中位置坐標與作圖法獲得準確坐標對比分別如圖5中（1,2）、（2,2）所示。

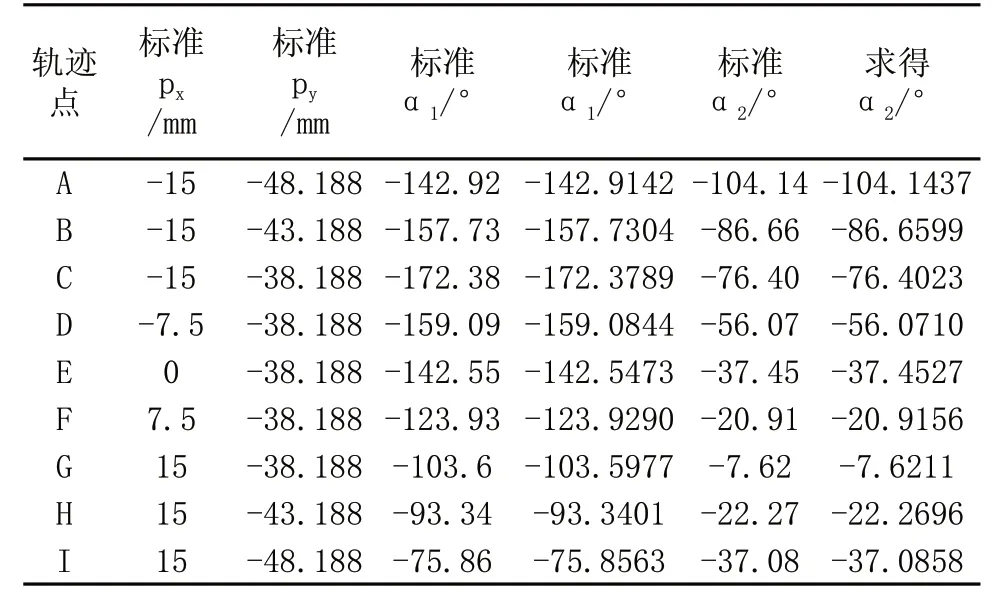
表3 末端軌跡點轉角對比相關參數表

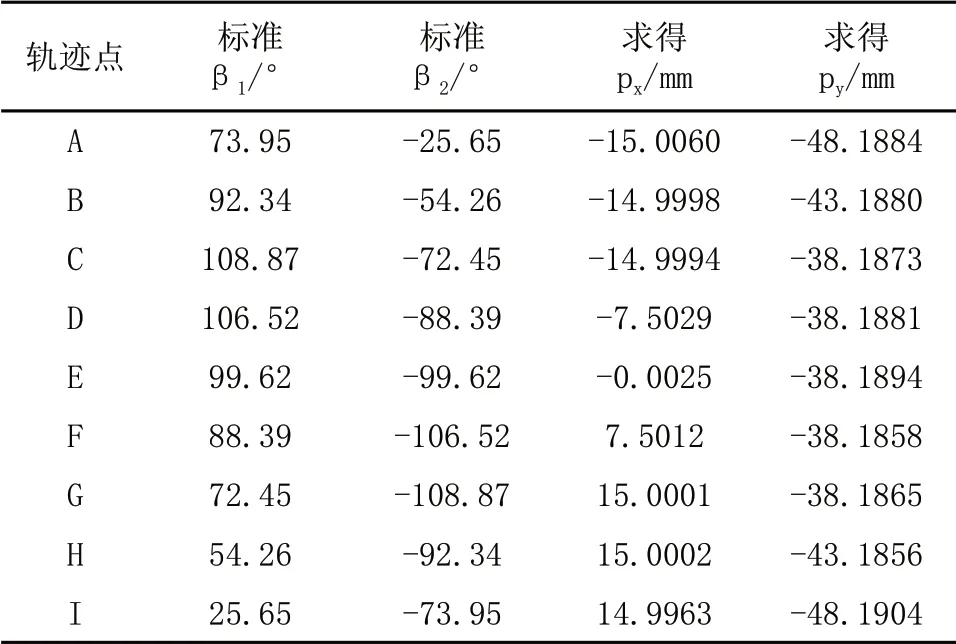
表4 末端點位置對比相關參數表

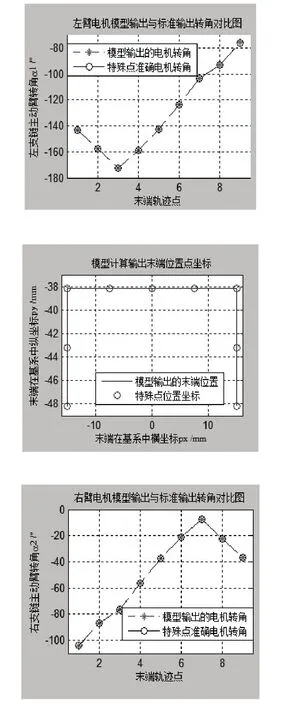
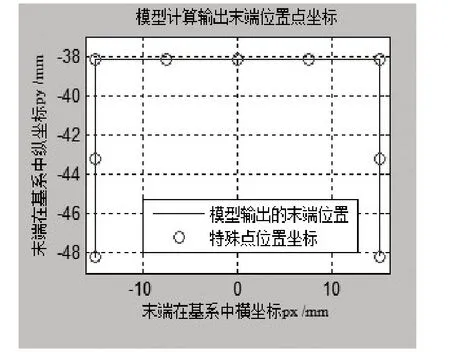
圖5 主動臂轉角及末端軌跡對比圖

由表3、表4及圖5可以看出通過模型求得主動臂轉角、末端點位置分別與標準轉角及標準末端位置值吻合一致，證明了模型建立的正確性。

3 結論

總觀整個求解過程，對兩個及以上自由度機械手只需確定相應的連桿參數通過矩陣坐標變換即可求得機械手末端位置逆解表達式。相比以往大多采用的幾何法，D-H參數法不必尋找連桿間幾何位置關系（自由度越多，幾何關系越復雜，建立模型的難度就越大），關節轉角滿足右手法則即可，具有更好的適用性。同時可以大大的縮短企業對滿足特定需求的機械手的研制周期，具有重要的現實意義。

[1] 梅江平,王攀峰,倪雁冰.二平動自由度高速并聯機械手位置控制[J].組合機床與自動化加工技術,2004,04(7):7-8.

[2] 李占賢,黃田,梅江平.二平動自由度高速輕型并聯機械手控制技術研究[J].機器人,2004,26(1):63-65.

[3] 許禮進,劉有余,劉陽.DELTA機器人逆運動學的分析與控制[J]. 制造業自動化,2014,36(9):66-67.

[4] Alain Codourey. Dynamic Modeling and Mass Matrix Evalution of the DELTA Parallel Robot for Axes Decoupling Control[J]. Institute of Robotics,1996:1211-1212.

[5] 梁香寧.Delta機器人運動學建模及仿真[D].太原:太原理工大學,2008:7-19.

[6] 李占賢.高速輕型并聯機械手關鍵技術及樣機建造[D].天津:天津大學,2004:14-17.

[7] Maira M.da Silva, Leopoldo P.R.de Oliveira, Olivier Bruls etal. Integrating structural and input design of a 2-DOF highspeed parallel manipulator: Aflexible model-based approach[J]. Mechanism and Machine Theory,2010,45:1509-1511.

[8] John J. Craig. Introduction to Robotics: Mechanics and Control [M].Third Edition. Beijing:China Machine Press,2005:19-128.

[9] 蔡自興,謝斌.機器人學[M].第三版.北京:清華大學出版社,2015, 19-60.

[10] 張福學.機器人技術及其應用[M].北京:電子工業出版社, 2000:165-219.

[11] Stefan Staicu. Matrix modeling of inverse dynamics of spatial and plannar parallel robots[J]. Multibody Syst Dyn,2012,27:240-244.