二階滑模控制方法及其對環形倒立擺的控制應用
孫靈芳,邢 宇,李 斌
SUN Ling-fang, XING Yu, LI Bin
(東北電力大學 自動化工程學院,吉林 132012)
0 引言
滑模控制方法是在二十世紀60年代由前蘇聯學者Utkin和Emelyanov提出的一種控制方法,實質上是一種非線性的控制,表現為控制的不連續性.該控制特性可以迫使系統在在一定特性下沿規定軌跡作小幅度、高頻率的上下運動[1]。這種控制的不連續性表現為不連續的控制量出現在滑模變量s的一階導數中,所以稱傳統滑模為一階滑模。滑模變量的一階導數的不連續性導致滑模控制存在“抖振”現象,這在實際工作中具有很大的危害.近幾十年來,科研工作者們一直在尋找抑制“抖振”現象的方法,如“邊界層”法、濾波方法、高為炳提出的“趨近律”法等。在此期間,由Levant提出的高階滑模控制方法得到了廣泛的關注.高階滑模不但可以保持傳統滑模具有的優點,而且可以有效地抑制了傳統滑模控制產生的“抖振”,從而提高了控制的精度[2]。
1 高階滑模的定義
首先介紹滑動階(Sliding Order)的定義[3]:
定義1 滑動階r是指滑模變量s的連續全導數(包括零階) 在滑模面s=0上為0的數目.
高階滑模的定義是由Levant和Firdman在1966年給出的,如下:
定義3 對于一個光滑的動態系統,滑模面s為光滑函數,r階滑動集是非空的,并且由不連續動態系統的Filippov軌跡組成,則滿足相關運動稱為關于滑模面 0),( =xts 的“r階滑模”。
2 二階滑模控制
根據高階滑模的定義可以知道,當且僅當系統軌跡位于狀態空間s=0和交界處時,系統具有二階滑模動態。
最早使用的高階滑模控制就是二階滑模控制,近幾年,二階滑模仍然運用非常廣泛,者正是由于二階滑模控制的控制器結構簡單,并且所需要的信息量不多。常見的二階滑模控制算法有三種,分別是螺旋(Twisting)算法、超螺旋(Super-Twisting)算法和給定收斂律(Prescribed Convergen Law)算法[4,5],下面主要介紹超螺旋算法。
2.1 問題描述
考慮如下非線性系統:
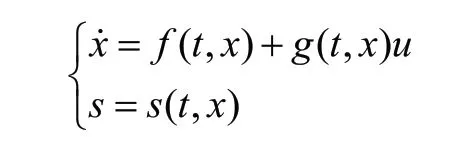
其中 ∈x Rn為系統狀態量, ∈u R為控制輸入,f(t,x)和g(t,x)為不確定光滑函數,s=s(t,x)為滑模面。二階滑模控制的目標是使系統狀態在有限的時間內到達滑模面s=s(t,x)并且具有二階滑動模態。
2.2 超螺旋(Super-Twisting)算法
超螺旋算法與其他二階滑模算法相比存在著特殊之處,它僅僅需要滑模變量s的信息,而且當控制系統的相對階為1時,利用超螺旋算法可以避免抖振。它的相軌跡是在 sso˙相平面上繞原點螺旋扭轉,在有限的時間內收斂到原點。
超螺旋算法的控制器由兩個部分組成,其中第一部分為其對時間不連續的導數項,第二部分為滑模變量s的連續函數,控制器的具體形式如下:
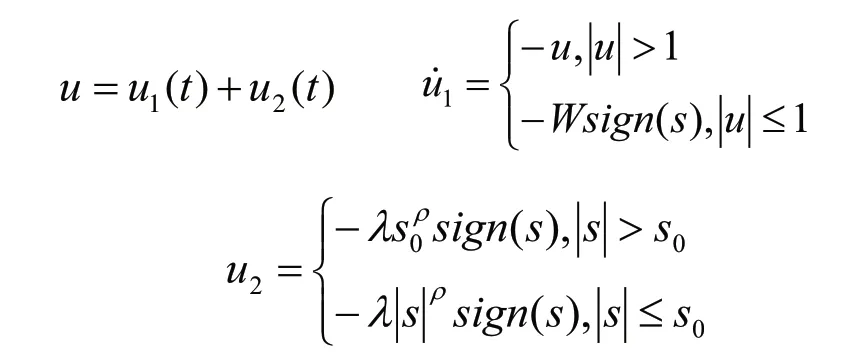
為了保證算法在有限時間收斂,則應滿足以下條件:
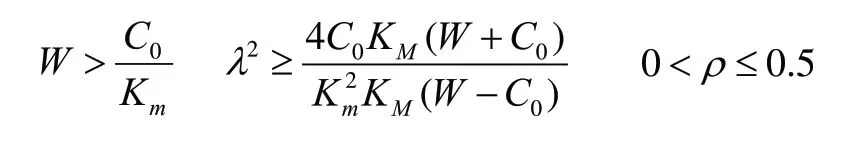
3 單級環形倒立擺的建模
倒立擺往往用來驗證一種理論的正確性和在實際應用中的可行性,是一個非線性、不穩定的被控對象。目前有許多對小車驅動直線倒立擺的控制研究,但是這種直線倒立擺有很多傳動裝置,存在誤差導致實驗失敗。與此相比,環形倒立擺沒有小車的拖動和連桿的行徑限制,所以對于控制情況來說有很大的改善。

圖1 環形倒立擺模型示意圖
單級環形倒立擺模型由一個連桿、一個擺桿和一個質量塊組成[6,7],如圖1所示。其中θ1為連桿與水平Y軸的夾角,θ2為擺桿與垂直方向上的夾角,順時針為正。在距離擺桿轉動中心l處取一小段dl,這一小段的坐標為:

則這一小段的動能為:
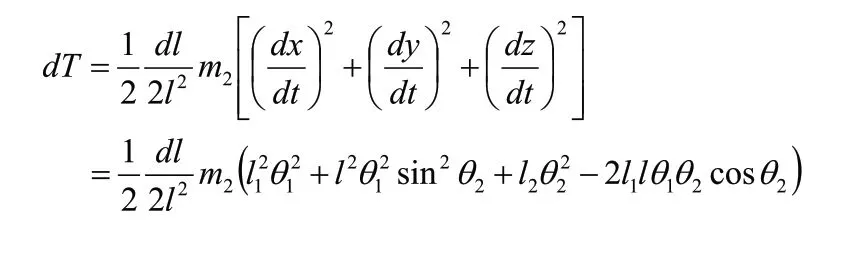
系統的總動能為:

其中Tm1代表連桿動能,為:
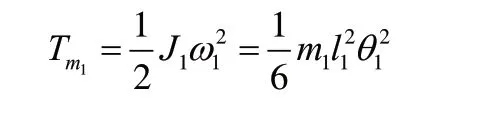
Tm2代表擺桿動能,為:
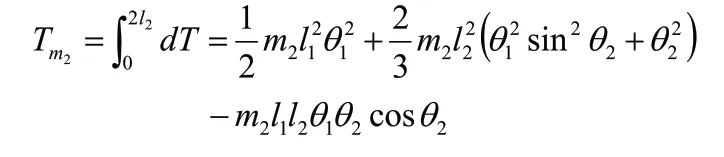
Tm3代表質量塊動能,為:
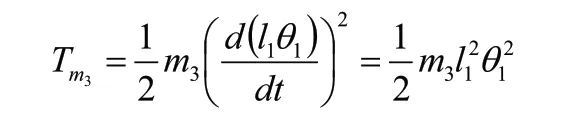
以擺桿靜止下垂時的質心為0勢能位置,則系統的勢能為:
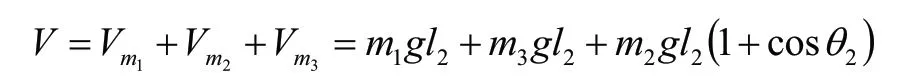
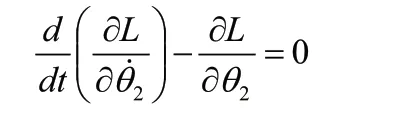
可以解得:
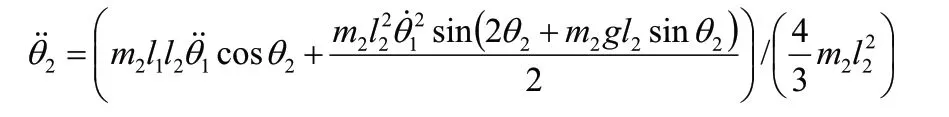

表1 參數物理意義及數值
將式在平衡位置進行泰勒級數展開并線性化[7],令會得到狀態空間方程如下:其中:
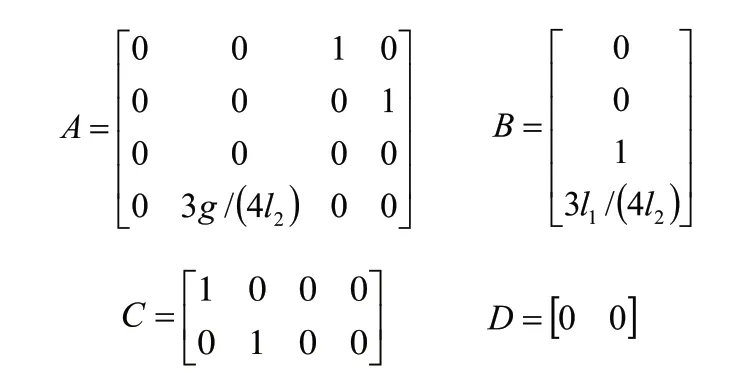
4 環形倒立擺的起擺及穩定控制仿真結果
在使用滑模變結構控制控制被控對象時,需要做兩部分工作:第一部分是控制器的設計;第二部分為滑模面的設計。本文使用超螺旋算法的控制器,下一步就是對控制器中的滑模函數s進行設計以達到控制需求。
1)設計滑模函數為:
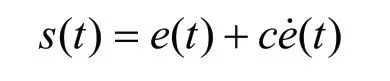
其 中c 必 須 滿 足Hurwitz 條 件,即c >0,為理想的角度信號。
經過不斷的試驗,取參數w=2,s0=100,λ=500,ρ=0.5,c=0.05,Simulink仿真模塊如圖2所示。
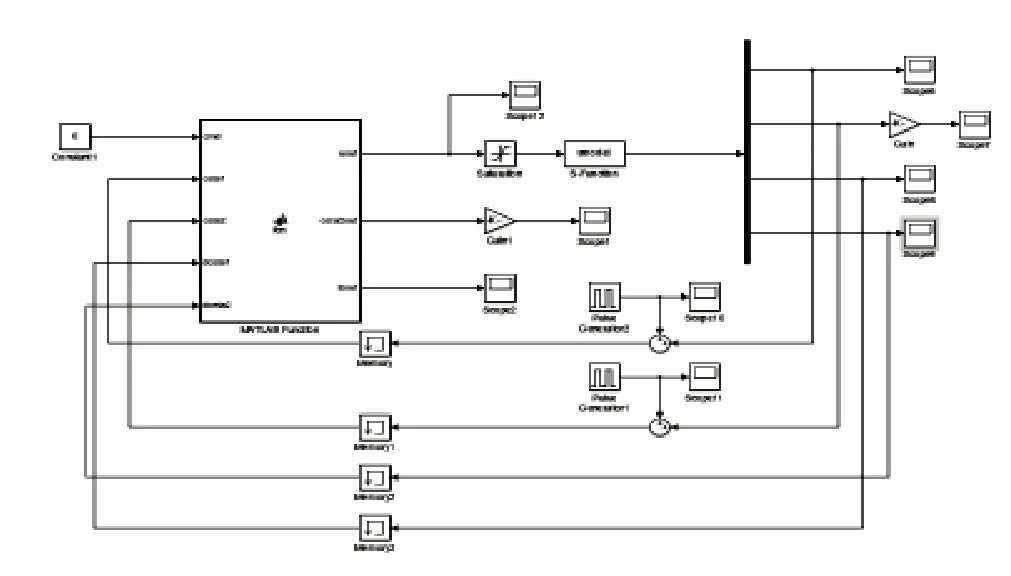
圖2 Simulink仿真模塊圖
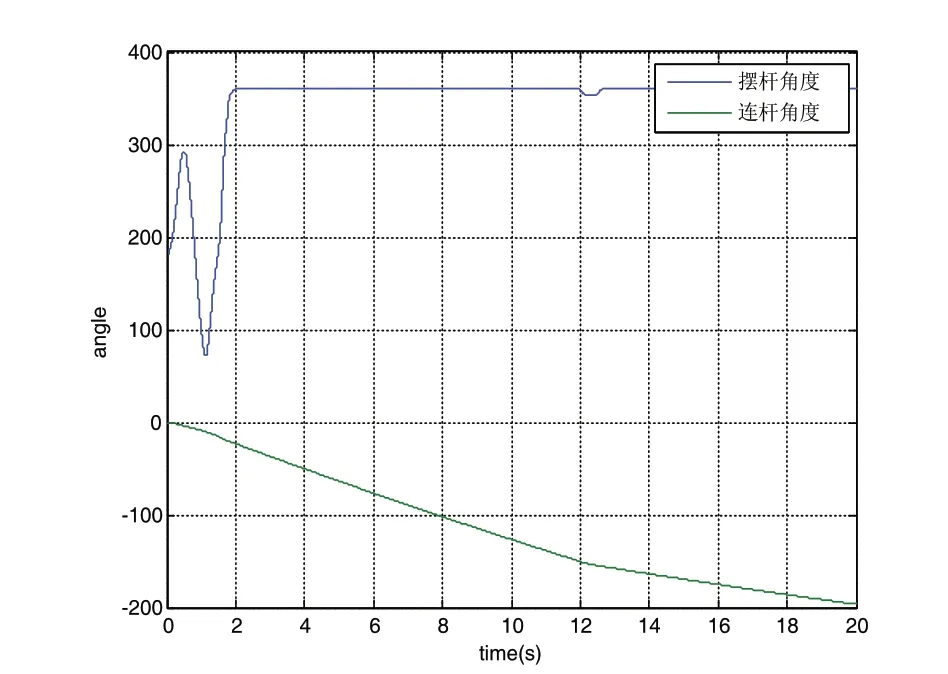
圖3 擺桿、連桿角度仿真曲線
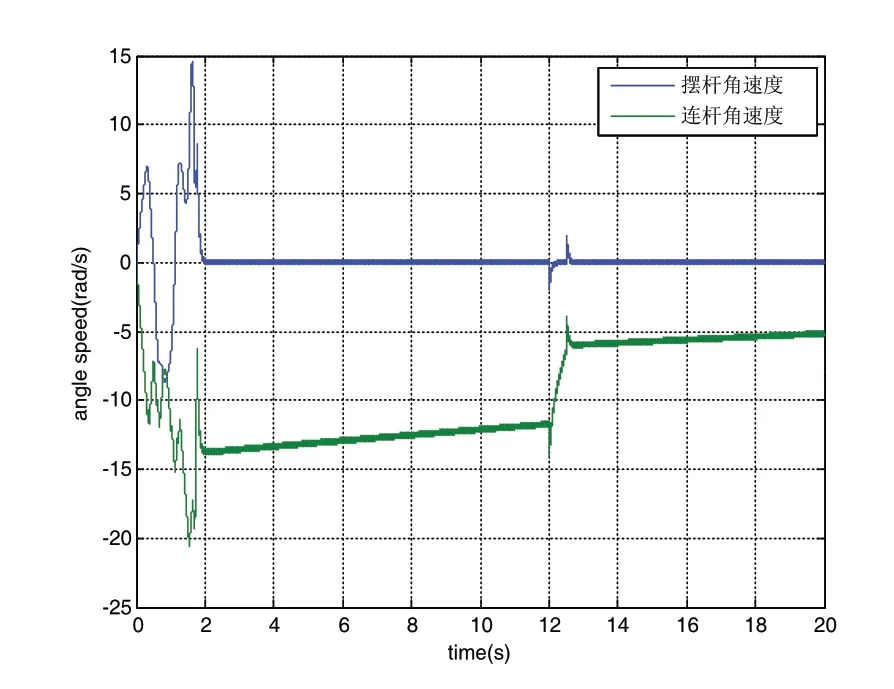
圖4 擺桿、連桿角速度仿真曲線

圖5 控制仿真曲線
由仿真結果可以看出,利用超螺旋算法的控制器可以使擺桿角度豎直穩定,起擺時間2s左右,并且2s后穩定,在第12s加入干擾脈沖,在小于1s內恢復平衡,魯棒性較好。但是結果同樣可以看出不能保證連桿角度穩定,由連桿的角度與連桿的角速度曲線可以明顯看出被控量發散,不能保證穩定且控制量抖振較大。
2)采用Ackermann公式設計滑模函數[8,9]:
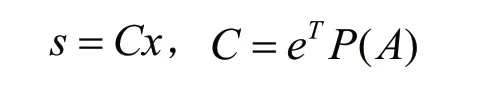
Ackermann公式描述為:
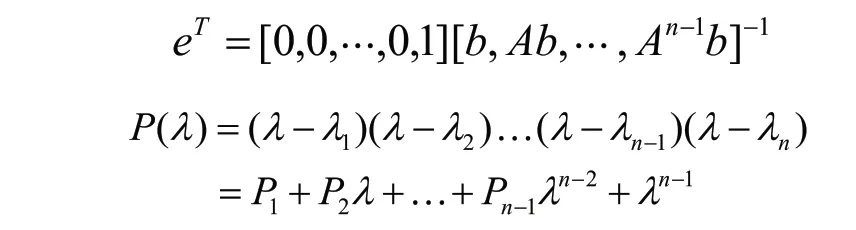
矩陣A和向量b由系統的狀態空間方程得到,此時向量b即是系統狀態空間方程中的矩陣為系統的特征多項式,是系統期待的特征值,從而可以算出C的值。
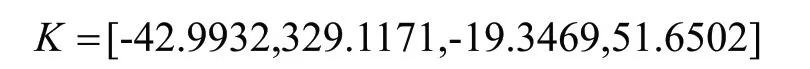
取參數 1=ω ,s0=500,λ=5,仿真結果曲線如下:

圖6 擺桿角度曲線圖
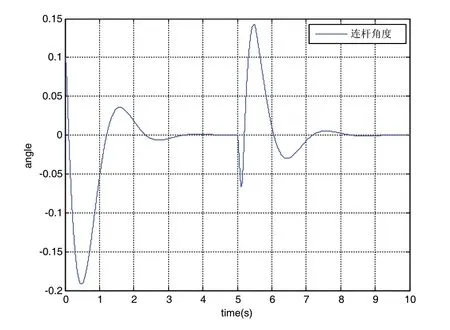
圖7 連桿角度曲線圖
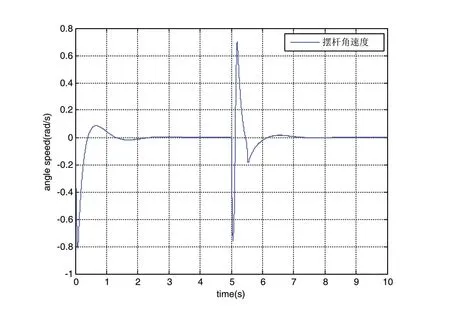
圖8 擺桿角速度曲線圖
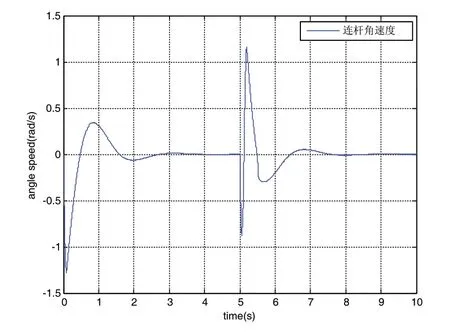
圖9 連桿角速度曲線圖
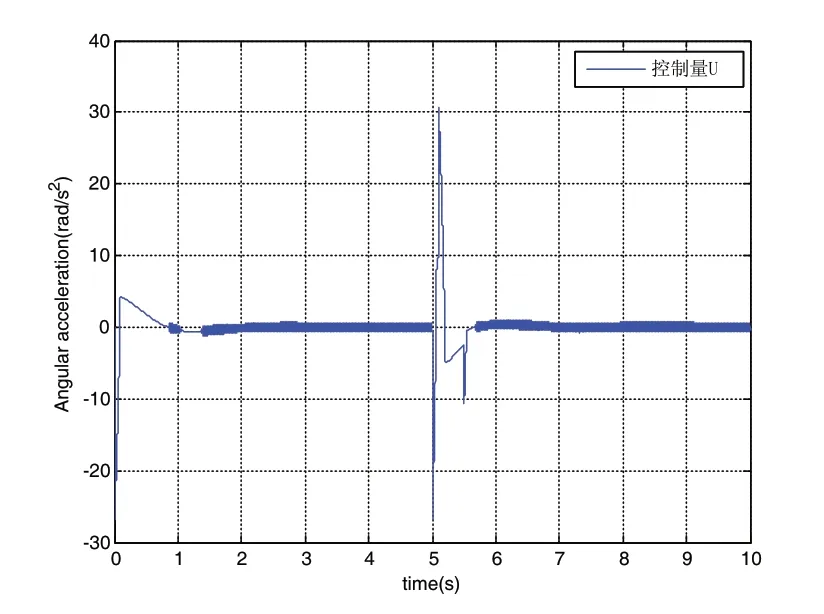
圖10 控制量曲線圖
由仿真曲線可以看出,利用Ackermann方法配置滑模面,可以保證四個被控量全部達到穩定狀態。在第5s時加入幅值為0.1,周期為10的脈沖信號作為干擾信號,由仿真結果可以看出:系統在2.5s左右可以快速穩定,相比較第一種滑模面,第二種穩定的時間大于第一種,但是超調量小于第一種使用滑模面的控制,并且抖振明顯減小。
5 結束語
本文利用了Lagrange方程完成了環形倒立擺的系統建模,使用了二階滑模超螺旋算法對環形倒立擺進行了簡單的控制。根據仿真結果,二階滑模控制克服了邊界層法犧牲系統魯棒性的缺點,保留了傳統一階滑模的主要優點和提高了控制精度,而且可以有效地削弱抖振.但是用二階滑模控制器時,主要的困難是如何讓調整不同算法的參數,盡管這樣,二階滑模控制仍然可以解決一大類控制問題。
[1] 劉金琨,孫富春.滑模變結構控制理論及其算法研究與進展[J].控制理論與應用,2007,24(3):407-418.
[2] Arie Levant.Higher order sliding modes,differentiation and outputfeedback control[J].Internation-al Journal of Control,2003,76(9--10):924-941.
[3] Arie Levant.Higher order sliding modes as an natural phenomenon in control theory[J].Robust control via variable structure an Lyapunov techniques,1996,217:107-133.
[4] Arie Levant.Homogeneity approach to high-order sliding mode design[J].Automatica,2005,41(5):823-830.
[5] Arie Levant.Principles of 2-sliding mode design[J].Automatica,2007,43(4):576-586.
[6] 王東亮,劉斌,張曾科.環形一級倒立擺起擺及穩定控制研究[J].微計算機信息,2007,23(2-1),1-2.
[7] 張姝,朱善安.環形單級倒立擺起擺控制研究[J].江南大學學報(自然科學版),2004,3(5):482-485.
[8] 孟祥萍,薛昌飛,張化光.基于Ackermann公式的分散滑模負荷頻率控制[J].東北大學學報(自然科學版),2000,21(2):128-131.
[9] 彭亞為,杜彬,陳娟.基于Ackermann公式的滑模控制設計方法[J].北京化工大學學報(自然科學版),2011,38(4):128-133.

