自動袋裝物料裝車機結構研究與分析

黃金鳳，武金藝，李 煒，崔建國

HUANG Jin-feng, WU Jin-yi, LI Wei, CUI Jian-guo

（河北聯合大學 機械工程學院，唐山 063009）

0 引言

在水泥、飼料、糧食、化工等行業生產中，需要將袋裝物料碼放在運輸車輛上。目前，國內這些行業中大部分采用人工或叉車裝車，其過程效率低、勞動強度大、環境惡劣。隨著包裝裝備的自動化，包裝速度明顯提高，迫切需要一配套的自動裝車設備，但是所裝物料種類、物料碼放順序、包裝袋材料等眾多因素都制約著自動裝車設備的研發。

自動袋裝物料裝車機是針對現有技術缺陷，結合袋裝物料包裝運輸生產實際，提供的一種環保、高效、重載的袋裝物料裝車機。該裝車機易于維護，工作過程中最大化的減少揚塵的產生，實現環保裝車，并且料袋碼放整齊，可最大化的利用車廂空間。

1 總體介紹

1.1 自動袋裝物料裝車機總體方案

自動袋裝物料裝車機主要完成袋裝物料的裝車工作。根據物料裝載要求和生產廠家實際工況，裝車機總體結構方案如圖1所示，由導軌、移動天車、吊架、斜皮帶、撥盤、電動缸、裝車機械臂等部分組成，其中導軌、移動天車、斜皮帶是生產廠家原有設備。

在自動袋裝物料裝車機總體結構中，整個結構坐落在移動天車上，沿導軌平移，保證同步運動，以實現袋裝物料能夠沿車長方向依次碼放。吊架安裝在移動天車上，安裝架固定在斜皮帶上，電動缸上部采用虎克鉸與吊架配合，下部采用關節軸承與安裝架鉸接，通過電動缸的伸縮變換帶動斜皮帶上下動作，滿足物料逐層碼放要求，同時以克服工作過程中斜皮帶產生的左右搖擺的慣性力，確保裝車精度。斜皮帶前端安裝一套撥盤機構，撥盤利用物料袋下落的慣性將其分撥到左右兩側，初步實現袋裝物料的橫向平移。機械臂接取來自撥盤的袋裝物料并迅速送至指定位置。

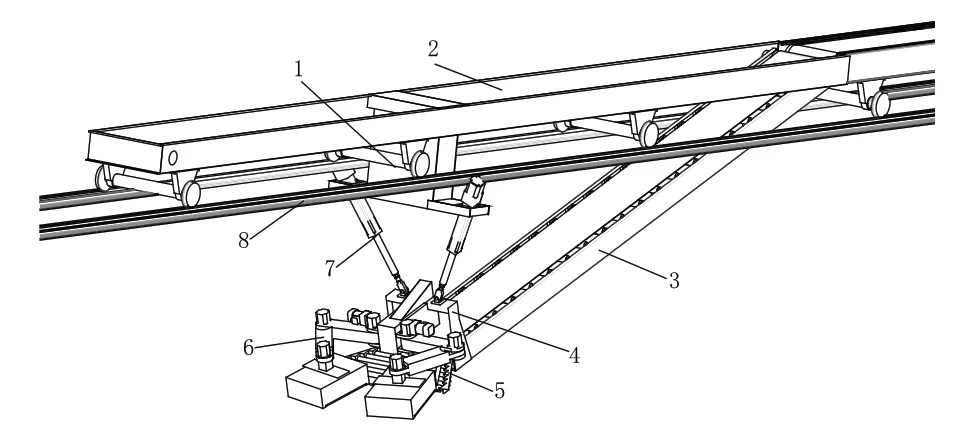
圖1 自動袋裝物料裝車機整體結構

1.2 裝車機械臂方案

裝車機械臂是袋裝物料自動裝車機的核心部分，直接決定著物料能否快速順利裝車，其結構示意圖如圖2所示。基于串聯機構的裝車機械臂，主要由基座、大臂、小臂及搬運廂等部分組成，各部分之間由肩關節、肘關節和腕關節相互連接，各關節采用伺服電機加諧波減速器結構，整個機械臂結構緊湊，易于控制。

依據物料行業的實際裝載要求，為提高裝車機械臂的工作靈活性，機械臂總體采用3自由度設計，且3個關節均為轉動關節。機械臂各關節上的伺服驅動電機，帶動機械臂的各個連桿在控制系統的作用下按已規劃好的運動軌跡運動，以實現末端搬運廂準確的裝卸袋裝物料至指定位置。為滿足袋裝物料的快速裝載要求，以及工作空間大的實際情況，自動袋裝物料裝車機的整體結構中采用了雙機械臂協調動作，提高裝載速度并擴大裝載范圍。機械臂關節主要尺寸參數如表1所示。

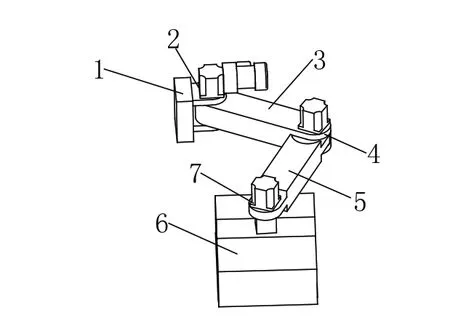
圖2 裝車機械臂結構

表1 裝車機械臂關節主要尺寸參數

考慮到自動袋裝物料裝車機繁重的工作狀況，惡劣的工作環境，及裝車機械臂快速的裝卸頻率，臂體在滿足強度、剛度要求的前提下，盡可能的選用輕型材料，以減小不必要的負重，減少附加慣性力。

2 裝車機械臂運動學分析

運動學分析在機器人學中占有非常重要的地位，機械臂運動學分析的主要內容是末端執行器的位姿與機械臂關節變量之間的關系[1]，主要分為兩大問題，即運動學正問題和運動學逆問題。根據機械臂各關節的轉角或位移推算出機械手末端執行器的位姿為運動學正問題，根據機械臂末端的位姿計算出各關節的轉角或位移為運動學逆問題[2]。

2.1 建立運動學模型

為了得到裝車機械臂的運動學方程，采用D-H參數法確定該機械臂的運動學模型。D-H法是由Denavit和Hartenberg于1955年提出的，是一種經典的研究機器人運動學的方法[3]。依據此理論將機械臂的基座、大臂、小臂、末端搬運廂抽象為連桿，并分別建立坐標系，建好的裝車機械臂坐標系如圖3所示。

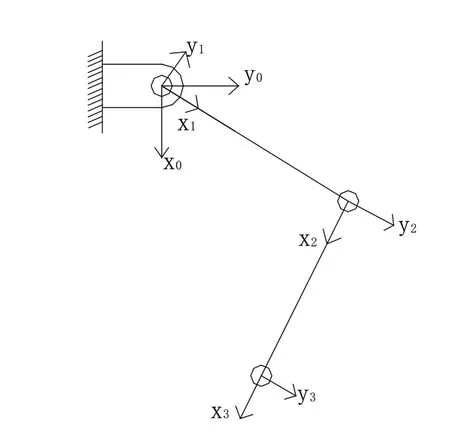
圖3 裝車機械臂坐標系

在坐標系確定之后，根據裝車機械臂的本體結構，確定各關節的D-H參數，確定的D-H參數如表2所示。

表2 D-H參數表

其中，αi-1為沿xi-1軸從zi-1移動到zi的距離；di為沿zi繞軸從xi-1移動到xi的距離；αi-1為繞xi-1軸，從zi-1旋轉到zi的角度；θi為繞zi繞軸，從xi-1旋轉到xi的角度。

2.2 運動學正解分析

機械臂正解分析主要建立機械臂的運動學方程以及求解末端執行器的位姿[4]。對于3自由度的裝車機械臂其運動學方程為：

其中A1、A2、A3各矩陣分別表示第i個連桿相對于第i-1個連桿的齊次變換。

根據已建立的裝車機械手D-H參數坐標系和參數，由機械臂的空間坐標變換方法得到連桿的D-H坐標變換矩陣公式(2)[5]，依據式(2)完成坐標系i-1和i之間的變換。

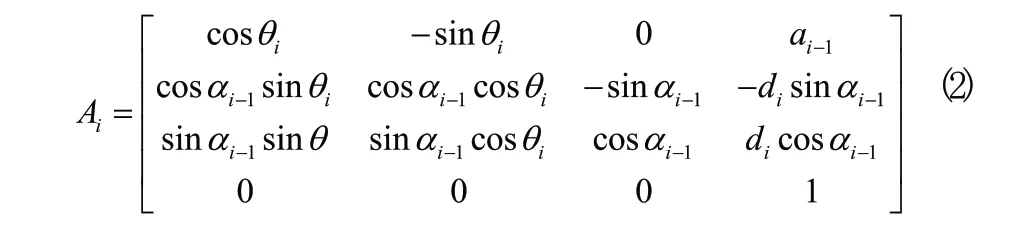
將表2中機械臂各關節連桿參數代入公式(2)中，得到各個變換矩陣如下：

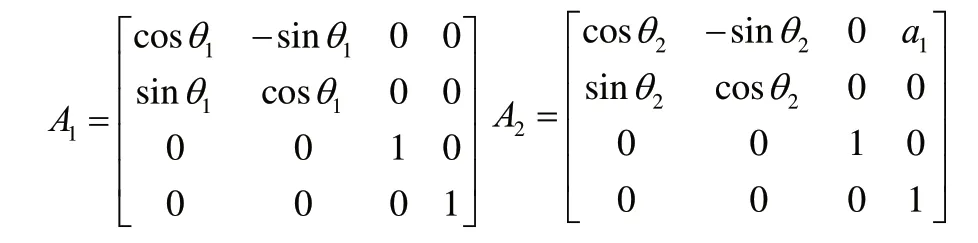
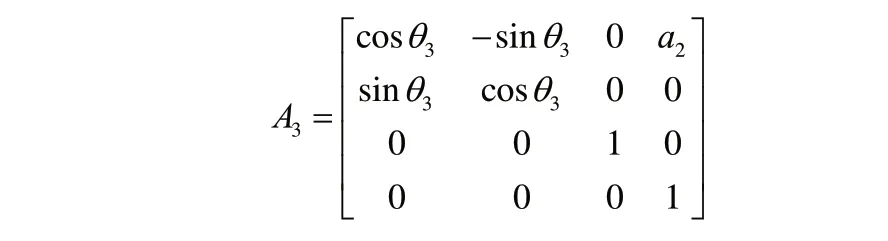
因此裝車機械臂的運動學方程為：

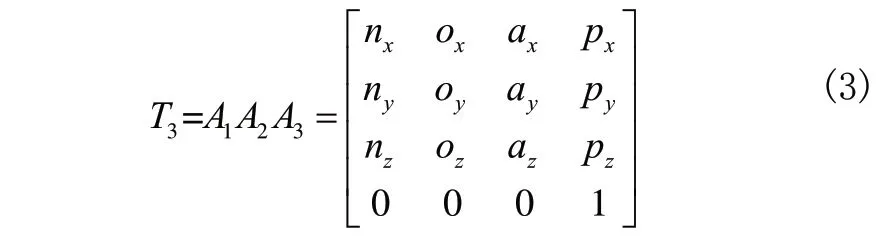
其中：

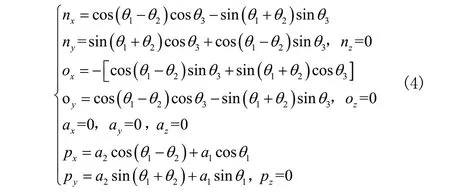
驗證正解的正確性是非常有必要的[6]。初始位置θ1=90°，θ2=0°，θ3=90°時，代入式(3)，計算機械臂運動學方程結果為：

該計算結果符合機械臂實際位姿。

當大臂轉過90°時，θ1=0°，θ2=0°，θ3=90°代入式(3)，計算機械臂運動學方程結果為：

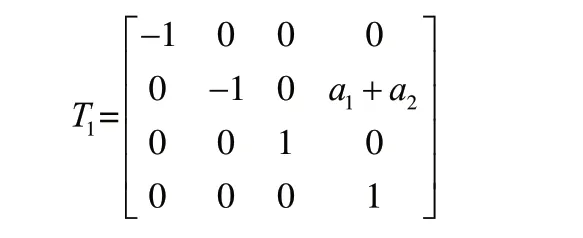
該計算結果符合機械臂實際位姿。

上述驗證表明機械臂末端執行器的位置坐標相對于基坐標系，x方向由大臂和小臂總長變為零，y方向由零變為大臂和小臂總長，z方向沒有變化，與機械臂實際運動情況相符。表明運動學方程的正確性。

通過以上運動學正解分析可以看出，末端執行器（搬運廂）的位姿向量為裝車機械臂關節轉角θ的函數，當給定3個關節的轉角θ1，θ2，θ3后，就可以按式(4)計算出末端執行器位姿和位置矢量，即確定裝車機械臂的末端執行器坐標系相對于基坐標系的位姿，得到機械臂運動學正解[7]。

2.3 運動學逆解分析

機械臂逆解分析主要是在末端執行器所要達到的目標已知的情況下求解各個關節變量，以驅動各個關節的電機，使末端執行器的位姿得到滿足[8]。對于3自由度的裝車機械臂來說，就是已知連桿的參數值和矩陣T3中的各個元素，求得相應的關節轉角θ1、θ2、θ3。

機械臂運動學逆解的分析方法有多種，主要有幾何法、解析法和數值法等[7]。幾何法即利用平面幾何關系求出它的運動學反解，幾何法分析運動學逆解比較直觀，可以減少分離變量法中復雜龐大的計算量，因此本文采用幾何法求解機械臂的運動學反解[9]。

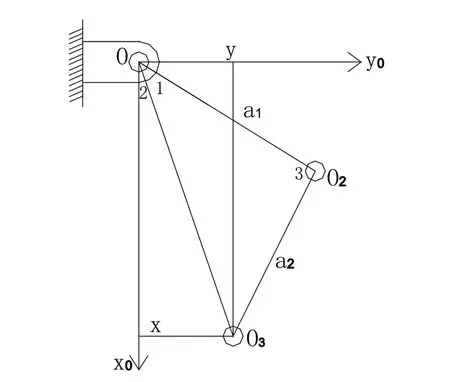
圖4 機械臂運動學逆解幾何法

如圖4所示，為了保證解存在，目標點(x,y)應滿足條件：

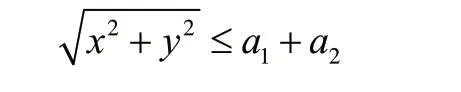
在O1，O2和O3組成的三角形內，應用余弦定理可得，

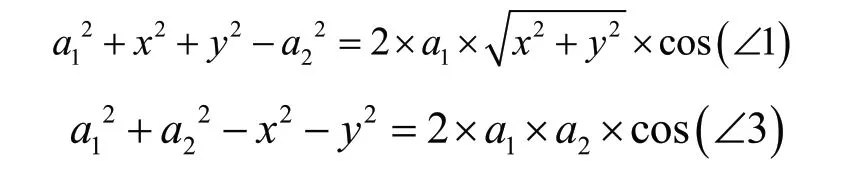
由此可得：

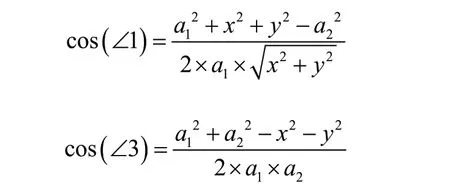
在滿足解的存在性的前提下，可能存在兩個解的情況：

因此：

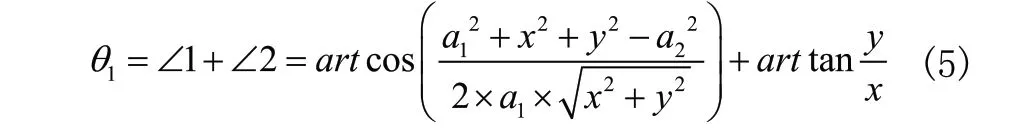
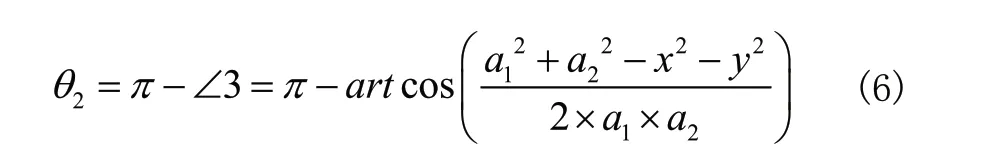
末端執行器（搬運廂）的方位角α由三個旋轉關節角度之和確定，即：

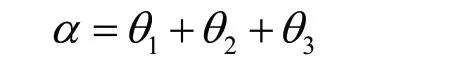
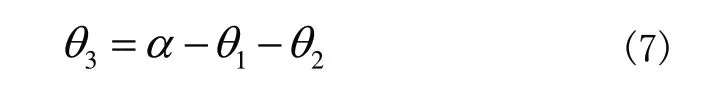
因此，當裝車機械臂的末端執行器要達到的目標位置已知時，代入式(5)～式(7)即可計算得到機械臂各個關節變量，從而得到裝車機械臂的運動學逆解。

3 裝車機械臂運動學仿真

根據生產廠家實際生產環境及袋裝物料裝載運輸過程中的實際要求，串聯的裝車機械臂只能沿特定的軌跡路線運動，為此根據物料裝載作業任務的要求進行軌跡規劃，規劃出機械臂預期的運動軌跡并進行仿真[10]，將結果以圖形的形式反映出來，得到機械臂直觀的運動情況。

袋裝物料裝載運輸過程中的實際要求及主要裝載參數如下所示：物料袋的外形尺寸為750mm×450mm×150mm；物料質量約為50千克/袋；物料包裝機打包速度1.5秒/袋；裝載車輛的車廂體積約為12m×2.3m×1.8m。

另外，裝車機總體結構的幾何安裝尺寸如下：雙機械臂的安裝間距500mm；機械臂與安裝架距離800mm；機械臂與撥盤垂直距離200mm；小臂末端安裝于搬運廂的頂部中心處。

針對物料裝載作業過程規劃末端搬運廂的x方向、y方向位移以及z方向轉角的仿真參數和時間，如表3～表5所示。

表3 搬運廂在x方向位移及時間規劃

表4 搬運廂在y方向位移及時間規劃

表5 搬運廂在z方向轉角及時間規劃

在此僅列出末端搬運廂的位置、速度、加速度的仿真曲線圖，如圖5～圖10所示。

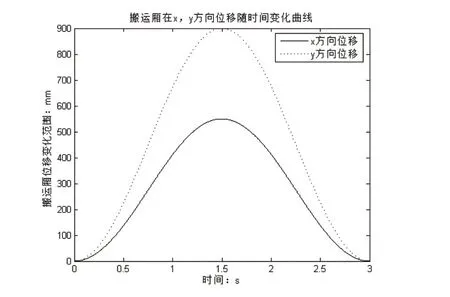
圖5 搬運廂x和y方向位移變化規律

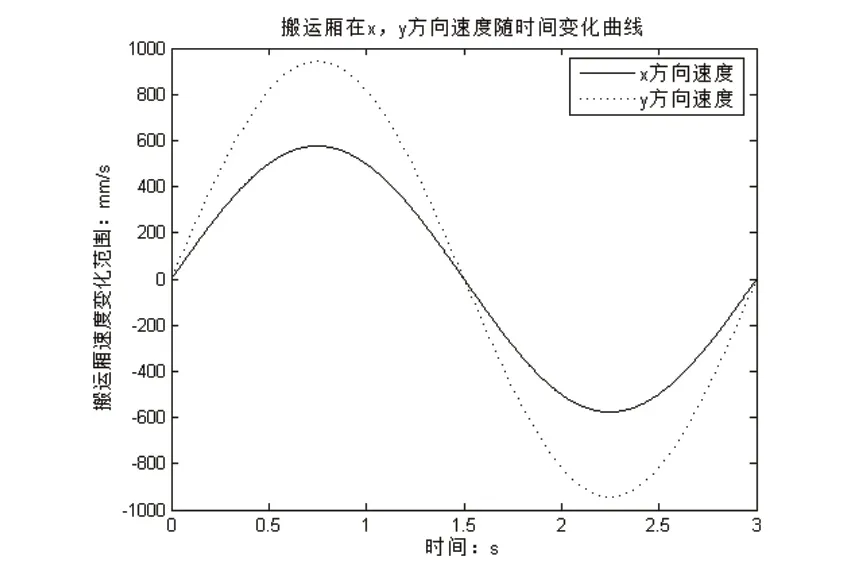
圖6 搬運廂x和y方向速度變化規律

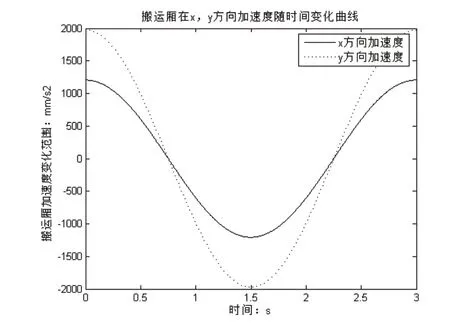
圖7 搬運廂x和y方向加速度變化規律

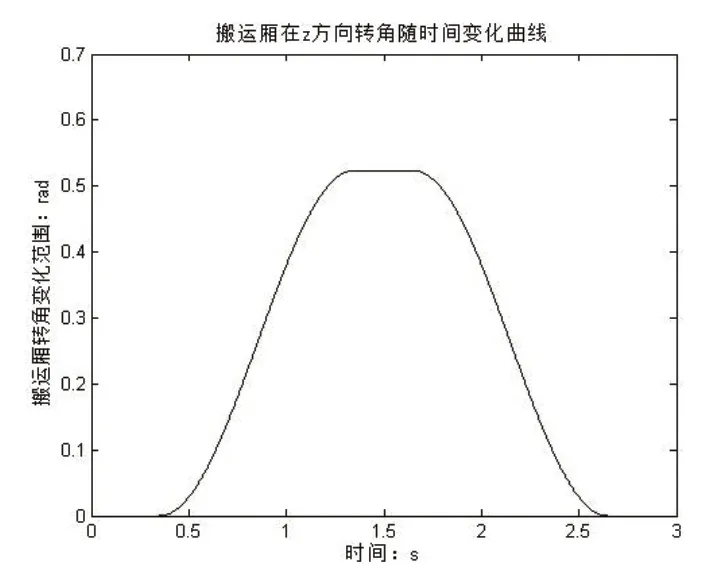
圖8 搬運廂z方向角度變化規律

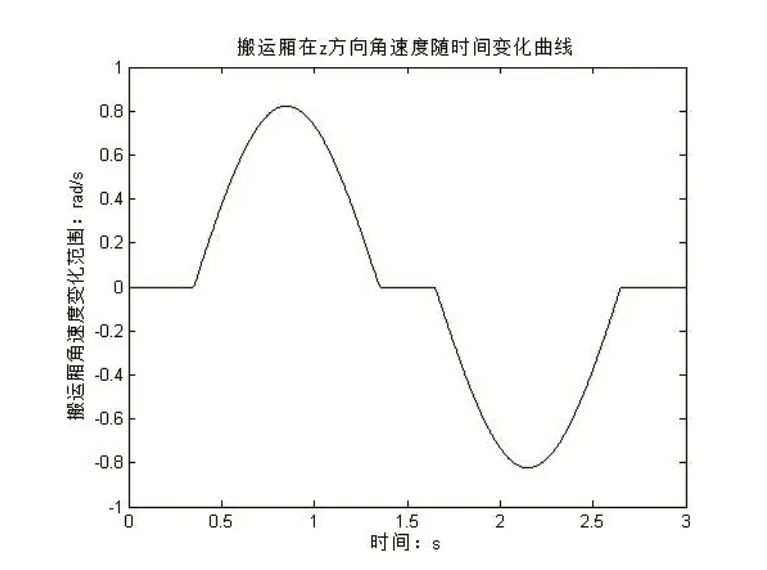
圖9 搬運廂z方向角速度變化規律

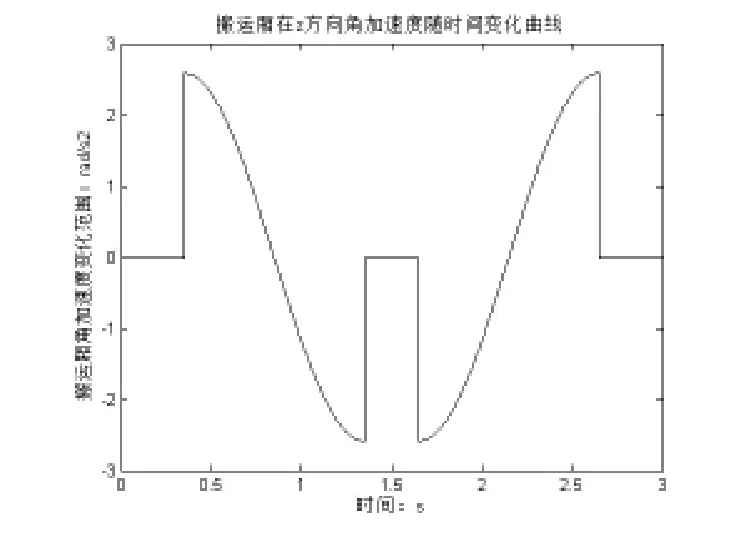
圖10 搬運廂z方向角加速度變化規律

通過末端搬運廂的仿真結果，可以看出在袋裝物料裝載操作過程中，搬運廂在x和y方向的位移變化量和z方向的轉角變化量均比較小，且速度、加速度變化平穩，變化范圍小，無突變，不會對機構產生沖擊，符合實際裝載條件，且表中具體數值為驅動伺服電機型號的選取提供理論數據。同時，搬運廂三方向位移、速度和加速度變化符合理論規劃，滿足設計要求，驗證了機械結構設計的合理性與可行性。

4 結論

1）根據袋裝物料行業實際需要，提出一種自動袋裝物料裝車機，研究分析其工作原理，并研發了串聯的裝車機械臂，該裝車機結構簡單，易于維護，工作空間大。對于串聯機械臂應用D-H參數法對其進行了運動學分析得到運動學正逆解。

2）利用MATLAB軟件使機械臂按照規劃好的裝載軌跡進行運動學仿真分析，得到構件的運動特性，驗證了運動學理論計算的正確性，表明了機構設計的合理性，為該機構的進一步研究和應用提供理論依據。

[1] 邢婷婷.上下料機械手的運動學及動力學分析與仿真[D].青島科技大學,2012.

[2] 楊麗,張鐵中.組培苗移植機器人的運動學求解[J].農業機械學報,2007,07:94-98.

[3] 張建業.力反饋主手機構設計若干關鍵問題研究[D].天津大學,2013.

[4] 劉振宇,趙彬,朱海波,鄒風山.六自由度機械臂分揀系統仿真平臺研究[J].機械設計與制造,2013,02:210-213.

[5] 楊文亮.蘋果采摘機器人機械手結構設計與分析[D].江蘇大學,2009.

[6] 李耀斌,趙新華.3-RRRT并聯機器人的位置正解研究[J].天津理工大學學報,2010,02:15-18.

[7] 胡飛,尹文慶,陳彩蓉.基于MATLAB的移栽機械臂運動學分析與仿真[J].江西農業學報,2012,12:151-153,157.

[8] 劉宏偉.基于ADAMS的五自由度機器人運動學仿真[J].機電產品開發與創新,2008,06:42-44.

[9] 范超.大型工業機器人操作臂機構設計與運動控制仿真[D].哈爾濱工業大學,2010.

[10] 趙獻丹,何慶中,趙虎,張良棟.基于Matlab和Pro/E的機械手運動軌跡仿真研究[J].煤礦機械,2010,06:60-62.