EMD分解與小波閾值聯合去噪在蔗地路譜信號處理中的應用

姜建瑋，李尚平，李 冰，解向陽

JIANG Jian-wei1, LI Shang-ping2, LI Bing1, XIE Xiang-yang1

（1.廣西科技大學 機械工程系，柳州 545006；2. 廣西民族大學，南寧 530006）

0 引言

對信號的去噪處理一直是信號處理領域的一個研究熱點。實際實驗測得的信號不可避免地都會有噪聲信號的引入，一旦噪聲污染達到一定的標準，會對后續的分析帶來嚴重的影響，導致后續工作的處理結果偏差過大或者直接導致結果錯誤，因此如何從采集的信號去除背景噪聲，獲得信號的真實信息，是一項非常重要的工作。傳統的去噪算法主要有傅立葉變換去噪法、Wiener濾波[1]、中值濾波[2]、小波變換去噪方法[3,4]等，進入二十一世紀以后，興起了EMD分解的信號去噪方法，很多學者陸續對其進行相關改進，使得這種去噪方法越來越在信號處理中受到學者們的青睞。本文結合了小波閾值去噪和EMD分解兩種去噪方法對項目前期所采集的蔗地路面譜隨機激勵信號進行去噪處理，對比之前的文獻，得到了蔗地路面激勵頻帶，同時對比了三種方法的去噪結果，驗證了本文使用方法的可靠性。

1 EMD分解基本理論[5]

EMD中文釋義為經驗模態分解，該方法適用于非線性、非平穩性信號，能夠把信號進行平穩化處理。其分解方法與傳統的傅里葉分析方法不同，該方法是基于信號的局部特性的一種信號處理方法。經過EMD分解后的信號會產生不同時間尺度的IMF分量，通過這種IMF分量能夠直觀真實的反應信號的特征，無論信號本身是線性或者非線性，是一種自適應分解方法。因此，在對非平穩性、非線性信號去噪時，EMD方法有著良好的處理效果和更大的優勢。EMD分解算法實際上是對信號的“篩分”過程。即對于原始信號x(t)，EMD分解產生各個IMF分量的過程如下[6]：

1）首先求出確定信號的所有局部極大值和極小值點，再采用三次樣條曲線把所有得出的局部極大值點連接起來擬合出極大值包絡Vmax(t)，所有得出的局部極小值點擬合出極小值包絡Vmin(t)，此時擬合出的極大值包絡和極小值包絡之間包含了信號所有的數據。

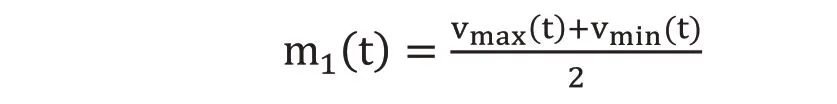
2）擬合完上包絡線Vmax(t)和下包絡線Vmin(t)以后，求出兩者的均值，可知：然后用原始信號x(t)減去求出的均值m1(t)，就得到一個去掉低頻分量的剩余分量h1(t)即：

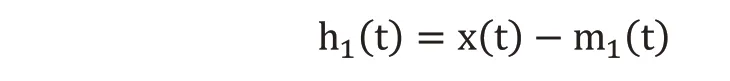
判斷剩余分量h1(t)能否符合固有模態函數定義的條件。如果符合條件，則這個剩余分量h1(t)作為一個IMF分量保存下來。

3）如果h1(t)不符合IMF定義的條件，則將h1(t)作為原始數據，重復2）～3）步驟，如下式：

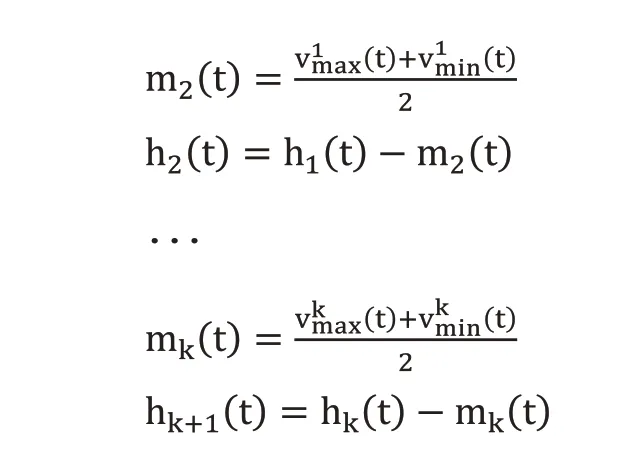
如果hk+1(t)符合固有模態函數成立的條件，則令：

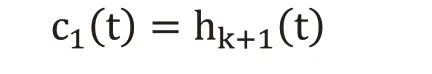
4）將原始信號x(t)分離出第一個IMF分量c1(t)，得：

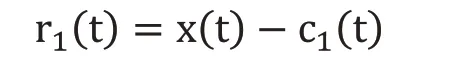
將r1(t)重新當作原始信號，然后重復步驟，得到第二個x(t)的IMF分量c2(t)，重復n次，直到得出第n次IMF分量cn(t)或者當殘差分量rn(t)是單調函數或者常數時，EMD分解過程終止。

最后，可用n階IMF分量和剩余殘差分量rn(t)擬合，從而構成原始信號x(t)，表示為下式：

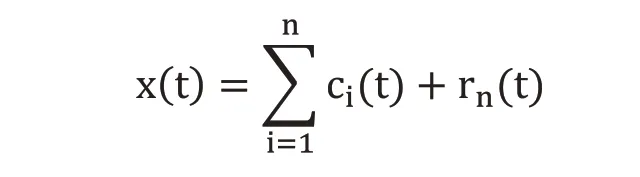
2 小波閾值去噪基本方法

使用小波分析可以將原始信號分解為一系列的近似分量和細節分量，信號的噪聲主要集中表現在信號的細節分量上。再使用一定的閾值處理細節分量后，經過小波重構就可以得到平滑的信號。在實際的工程應用中，有用信號通常表現為低頻信號或者是一些比較平穩的信號，而噪聲信號通常表現為高頻信號，所以，一般來說，一維信號的去噪可以分為以下三個步驟進行[7]：

1）信號的小波分解。選取小波基函數并需要決定分解層數。運用選取的小波基函數對信號進行固定層數的分解。

2）小波分解完成后，選擇一個閾值對得出的高頻小波系數采用硬閾值或者軟閾值的方式量化處理。

3）小波重構。根據小波分解后最底層的低頻系數與小波分解后產生的所有層的高頻系數，重構一維信號。

3 EMD分解與小波閾值聯合去噪

小波分析良好時頻性能非常適合處理非平穩信號，但是閾值的選取對信號去噪的效果影響差異比較大，而且在選用不同的小波基函數對信號的去早處理結果也會有較大的偏差，所以，小波變換的去噪方法雖然能夠對非平穩、非線性信號去噪，但是由于信號在去噪時要測試不同的小波基函數、閾值選取、尺度的選取等原因，使得去噪后的信號缺少了信號自身能夠表征的信息，不能夠很好地體現原始信號的自適應性。

EMD分解的實質是根據信號本身的內在特性而自適應地把非平穩、非線性的信號經過分解處理后得到各個線性和平穩性的IMF分量，因而不需要像小波變換一樣必須選擇合適的小波基函數。但在運用EMD算法進行去噪過程中，正如該算法的名字所言，其實質就是通過“經驗”選擇去除哪幾個IMF分量，同時保留哪幾個分量，從而達到去噪的效果。但是這種算法是一種“強制”去噪方法，眾所周知，實際的信號和大量的噪聲混雜在一起。因此，簡單地運用EMD去噪會很容易丟失含在噪聲當中的有效信息，不能較準確地得到有用信息。

針對上述兩種方法的局限性，本文對所采集的激勵信號采用EMD和小波聯合去噪的方法，可以相互彌補不足，使得去噪的結果更準確，對于這種方法目前已經有學者進行過相關研究，本文在東北石油大學的孫靈川的研究基礎上進行了這種方法的完善，對與分解后的IMF分量，對它們進行快速傅立葉變換，這樣可以了解具體各分量所在的頻率段，這樣更有助于個分量的篩選，同時對于低頻分量進行去除趨勢項和均值處理，去除采集時候的直流分量的影響。具體的去噪流程如圖1所示。

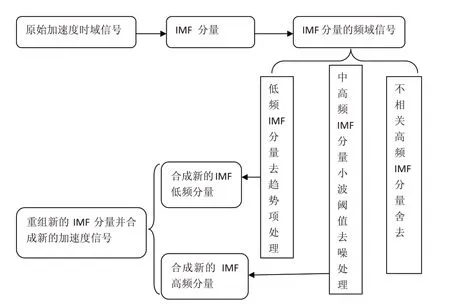
圖1 EMD分解與小波閾值聯合去噪流程

4 聯合去噪在蔗地路面激勵信號處理的應用

針對前期所采集的蔗地路面譜加速度響應信號，如圖2所示，現應用EMD分解與小波閾值聯合去噪對該時域信號進行去噪預處理，這對于后期路譜的位移信號擬合或者載荷譜信號編制的有效性有著不可或缺的作用。

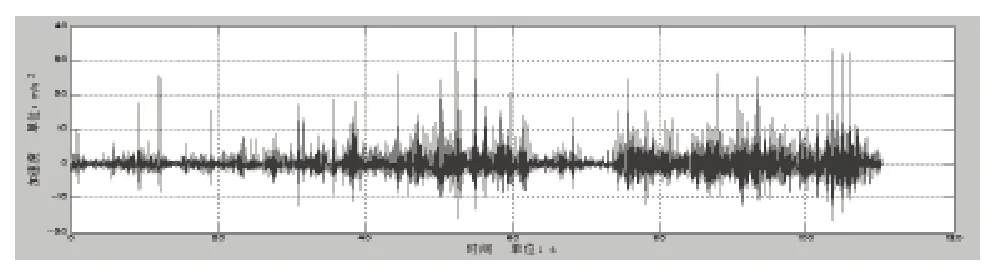
圖2 蔗地路面譜加速度響應信號

EMD分解以后的各個IMF分量如圖3所示。

由圖3可以知道，經過EMD分解以后，原始信號被分解成了十四個IMF分量，最后一個分量是殘余分量，為了更好的判斷個分量的頻域特性，圖4為各個分量進行FFT變換后的頻域特性。

從圖4可以發現，原始信號主要集中在0～10Hz之間，而第一、二階IMF分量頻率主要集中在10Hz以上，所以舍去第一階和第二階分量，而對于第三到第七階分量進行小波閾值去噪處理，這里選用小波基函數‘sym4’對信號進行4層分解，然后利用‘wdcmb’函數自動計算相應的閾值，并利用小波函數‘wdencmp’進行小波重構[8]，再對第八階到第十四階分量進行去除趨勢項和均值處理得到個分量如圖5、圖6所示，最后對去噪后的分量和去除均值和趨勢項的分量進行重組，從而得到完全去噪后的信號，圖5與圖6為利用上述方法去噪后的信號與原始信號的對比圖。

圖3 EMD分解后的各IMF分量

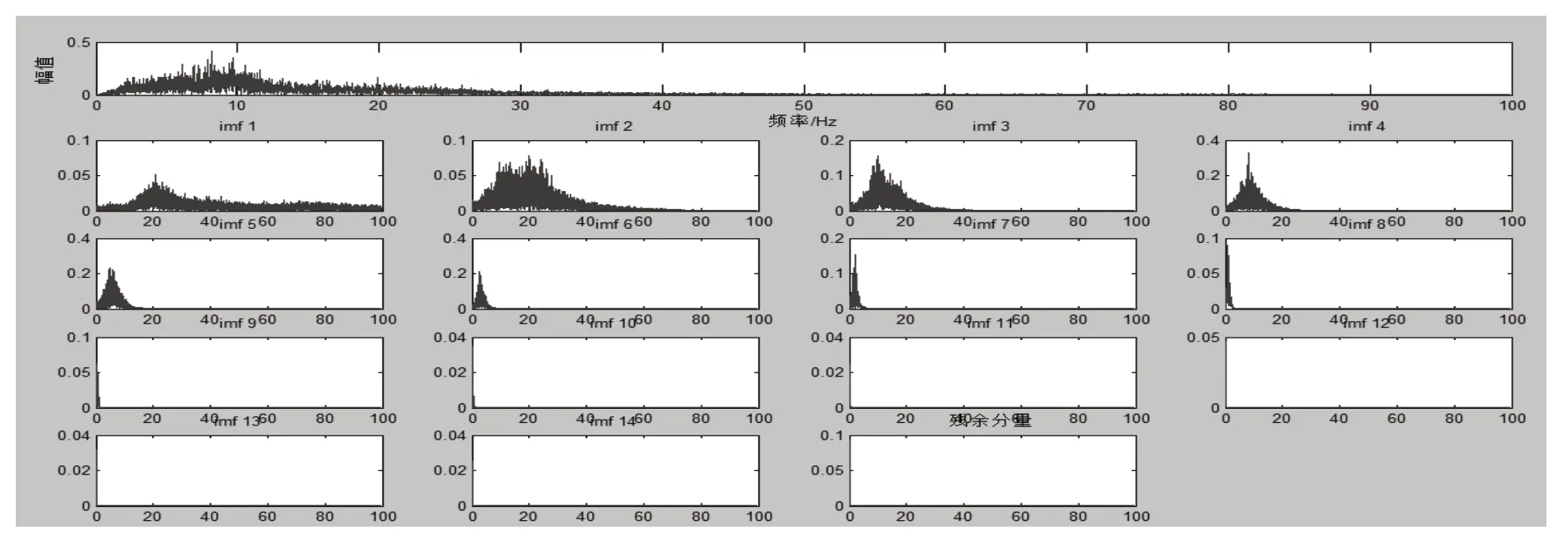
圖4 EMD分解后的頻域圖

圖5 去噪前后加速度時域對比圖

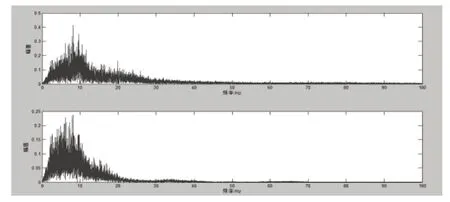
圖6 去噪前后加速度頻域對比圖

從頻域對比圖可以看到，對比原始信號的頻譜圖，去噪以后的頻譜圖頻率分布更集中，符合軟路面譜激勵頻率標準0～10Hz[9]，從去噪后的頻譜圖中可以看出，所采集的蔗地的路面激勵頻率主要集中在5Hz～10Hz之間。

5 結論

為了證明EMD分解與小波閾值聯合去噪在信號預處理中的優勢，下面利用三種方法分別針對蔗地路譜激勵信號進行去噪，其與原始信號的頻譜圖如圖7所示。

圖7 三種去噪方法與原始信號的頻譜對比圖

從上圖可以分析得知，小波閾值去噪由于閾值的自動選取不恰當導致在關鍵頻率下的振動幅度有所消減，而EMD分解去噪直接去除了高頻分量，分量直接進行重組，這樣得到的信號只是去除了高頻分量信號，相當于給了一個低通濾波，并沒有很好的達到去噪的效果，而聯合去噪很好的發揮了兩者的優勢，使得小波閾值去噪在EMD分解后的分量中有目的性的針對中低頻信號進行去噪，避免了由于閾值選取的不正確導致一些重要的低頻信號被剔除，盡可能的增加了去噪的準確度，效果顯著。

[1] 張賢達,保錚.非平穩信號分析與處理[M].北京:國防工業出版社,1998:25-80.

[2] 李士心.小波域中值濾波器設計的研究[J].電子科技大學學報,2003,3(雙l):19-21.

[3] 潘泉,孟晉麗,張磊,等.小波濾波方法及應用[J].電子與信息學報,2007,29(l):236-242.

[4] 文莉,劉正士,等.小波去噪的幾種方法[J].合肥工業大學學報:自然科學版,2002,25(2):167-172.

[5] 王婷.EMD算法研究及其在信號去噪中的應用[D].哈爾濱工程大學,2010.

[6] 李海濤,土成國,許躍生,等.基于EEMD的軌道-車輛系統垂向動力學的時頻分析[J].中國鐵道科學,2007(5):24-30.

[7] 王文圣,丁晶,向紅蓮.小波分析在水文學中的應用研究及展望[J].水科學進展,2002,13(4):515-520.

[8] 徐晨,趙瑞珍,甘小冰.小波分析?應用算法[M].北京:科學出版社,2004.

[9] GB/T 4970-1996.汽車平順性隨機輸入行駛試驗方法[S].中國標準出版社,1996:78-80.