數(shù)列單調(diào)性問題探究

☉遼寧省沈陽市教育研究院王恩賓

數(shù)列單調(diào)性問題探究

☉遼寧省沈陽市教育研究院王恩賓

這是一堂關(guān)于高三復(fù)習(xí)中數(shù)列問題的一個小的專題·該課對數(shù)列的單調(diào)性與函數(shù)的單調(diào)性進行了有機的結(jié)合，將二者的區(qū)別與聯(lián)系進行了剖析·利用信息技術(shù)將數(shù)列的單調(diào)性和函數(shù)的單調(diào)性進行了形象的描繪，在此過程中數(shù)形結(jié)合思想得到了滲透·通過對問題不同解法的探求，開拓了學(xué)生的視野，發(fā)散了學(xué)生的思維·通過編寫相似題型，激發(fā)了學(xué)生的學(xué)習(xí)潛力，拓寬了眼界，培養(yǎng)了創(chuàng)新能力和創(chuàng)新意識·

一、開場白

師：同學(xué)們好，前面已經(jīng)復(fù)習(xí)了函數(shù)和數(shù)列的基礎(chǔ)知識，對數(shù)列與函數(shù)有了比較深入的了解·數(shù)列和函數(shù)有著千絲萬縷的聯(lián)系，數(shù)列可以看作是一個函數(shù)，當(dāng)自變量為正整數(shù)（或它的有限子集）時，自變量從小到大依次取值時所對應(yīng)的一列函數(shù)值·因為從數(shù)列第二定義可以看出數(shù)列就是一列函數(shù)值，所以很多數(shù)列問題都可以借助函數(shù)的性質(zhì)進行解答·

二、鞏固基礎(chǔ)

師：在前面給大家的導(dǎo)學(xué)案中給出了學(xué)生自主學(xué)習(xí)的內(nèi)容，下面請各小組在小組內(nèi)用2分鐘時間交流、修正自主學(xué)習(xí)的問題，并請一名同學(xué)進行實物展示自主學(xué)習(xí)的第一個問題·

生1：我要展示的是自主學(xué)習(xí)部分的問題1·

問題1：數(shù)列的單調(diào)性的定義·

遞增數(shù)列的定義：如果數(shù)列｛an｝滿足an＜an+1，那么稱數(shù)列｛an｝為遞增數(shù)列；

遞減數(shù)列的定義：如果數(shù)列｛an｝滿足an＜an+1，那么稱數(shù)列｛an｝為遞減數(shù)列·

師：生1同學(xué)關(guān)于數(shù)列遞增、遞減的定義非常準(zhǔn)確，但有時在證明數(shù)列的遞增（或遞減）時還經(jīng)常應(yīng)用an-1＜an（或an-1＞an），此時一定要注意n≥2，n∈N+這一前提條件，即證明后一定要驗證n=1時結(jié)論是否成立，這是學(xué)生解題過程中經(jīng)常出現(xiàn)錯誤的地方，一定要引起足夠的重視·

生2：我要展示的是自主學(xué)習(xí)部分的問題2·

問題2：等差數(shù)列、等比數(shù)列的單調(diào)性·

數(shù)列單調(diào)性及其滿足的條件遞增數(shù)列，d＞0不增不減，d=0遞減數(shù)列，d＜0等比數(shù)列遞增數(shù)列，a1＞0，q＞1（或a1＜0，0＜q＜1）遞減數(shù)列a1＞0，0＜q＜1（或a1＜0，q＞1）等差數(shù)列

師：該同學(xué)很好地將等差數(shù)列和等比數(shù)列這兩個重要數(shù)列遞增、遞減的條件進行了整理，做的非常好·如果將等差數(shù)列、等比數(shù)列單調(diào)遞增、遞減的這些條件和結(jié)論通過圖像的形式進行記憶，那么效果會更好·如圖1所示，是老師作出的數(shù)列an=a1qn-1在a1＞1，q＞1時，條件、結(jié)論、圖像三者有機結(jié)合的一個反映數(shù)列單調(diào)遞增的圖像·請同學(xué)們課后用GeoGebra軟件將其他情況下數(shù)列增減性的圖像作出來·

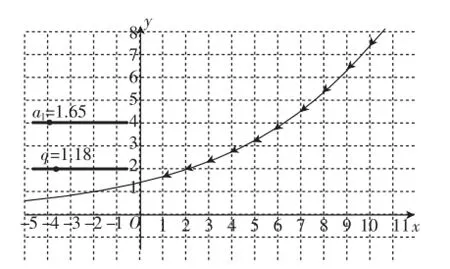
圖1

三、源于教材

師：導(dǎo)學(xué)案上兩個自主探究的問題都是選自教材上的問題，下面我們研究第一個問題·

問題3：（必修5P39）已知兩個等差數(shù)列的公差不相等，但第5項相等，這兩個等差數(shù)列中除了第5項外，還有序號相同且數(shù)值相等的項嗎？為什么？

生3：設(shè)等差數(shù)列｛an｝，｛bn｝的公差分別為d1，d2，且d1≠d2，a5=b5·假設(shè)兩個等差數(shù)列中除了第5項外，還有序號相同且數(shù)值相等的項，那么an=a5+（n-5）d1=bn=b5+（n-5）d2，得到d1=d2，與已知d1≠d2相矛盾·因此，兩個等差數(shù)列中除了第5項外，沒有其他序號相同且數(shù)值相等的項·

師：該同學(xué)利用反證法推導(dǎo)出等差數(shù)列不存在項數(shù)和項完全相同的情況，推理過程很嚴(yán)謹(jǐn)·還有沒有同學(xué)用其他方法解答此問題？

生4：因為等差數(shù)列an=a1+（n-1）d1=d1n+（a1-d1）可以看作是自變量為正整數(shù)（或有限子集）的一次函數(shù)（或常數(shù)），當(dāng)自變量從小到大依次取值時，對應(yīng)的是一列函數(shù)值，所以點（n，an）一定落在直線p：y=d1x+（a1-d1）上·

同理：點（n，bn）一定落在直線q：y=d2x+（a1-d2）上·因為兩個數(shù)列｛an｝，｛bn｝具有相同的第5項，所以直線p，q有一個交點（5，a5）·因為兩條直線在斜率不同的情況下最多只能有一個交點，不會有第二個交點，所以也不會存在這樣的數(shù)列，除了第五項之外再有序號相同且數(shù)值相等的項·

師：該同學(xué)將等差數(shù)列的通項公式與一次函數(shù)圖像有機地建立聯(lián)系，將抽象的代數(shù)問題幾何化，借助幾何圖形直觀形象地對問題進行了闡述·雖然沒有畫圖，但數(shù)形結(jié)合思想在解答中完美地得到了體現(xiàn)，值得鼓勵·

師：自主探究中還要求探究問題4·

問題4：（必修5P48）已知兩個等比數(shù)列的公比不相等，但第5項相等，這兩個等比數(shù)列中除了第5項外，還有序號相同且數(shù)值相等的項嗎？為什么？

生5：設(shè)等比數(shù)列｛an｝，｛bn｝的公比分別為q1，q2，且q1≠q2，a5=b5·假設(shè)兩個等比數(shù)列中除了第5項外，還有序號相同且數(shù)值相等的項，那么an=a5·qn-51=bn=b5·qn-52，得到qn-51=qn-52，如果n-5為偶數(shù)，那么q1=-q2是符合要求的，與已知q1≠q2不矛盾·

因此，兩個等比數(shù)列中除了第5項外，還有其他序號和數(shù)值均相等的項·

例如：等比數(shù)列an=2n-1，bn=（-2）n-1的奇數(shù)項相同，偶數(shù)項互為相反數(shù)·

師：圖2所示的是給出的公比互為相反數(shù)的兩個等比數(shù)列的圖像的對照圖·當(dāng)公比為負(fù)數(shù)時，對應(yīng)的數(shù)列為擺動數(shù)列，正負(fù)交替出現(xiàn)，圖中三角形點、圓形點部分分別為的圖像（注意三角形點和圓形點重合的點）·

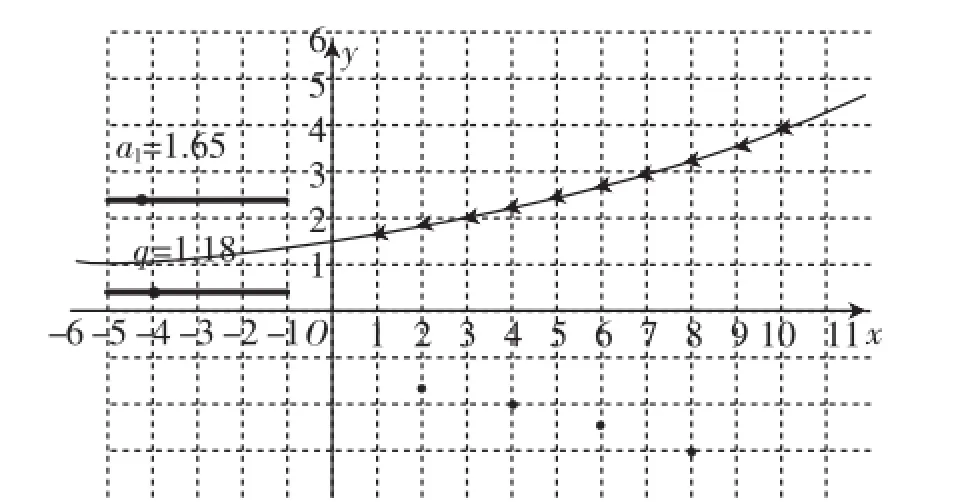
圖2

師：前面回顧了數(shù)列單調(diào)性的定義，下面用5分鐘時間結(jié)合數(shù)列單調(diào)性的定義各小組給出教材上問題5的不同的解題思路和解題方法·

問題5：（必修5P28）若數(shù)列｛an｝的通項公式是an=是第幾項？

生6：要判定數(shù)列項的最大值和最小值，可以先判定數(shù)列的變化規(guī)律，根據(jù)數(shù)列的變化規(guī)律再考慮數(shù)列的最大項和最小項·

師：該同學(xué)首先利用定義判定了數(shù)列的變化規(guī)律，再利用分離系數(shù)的方法確定數(shù)列各項的大小關(guān)系，推理過程嚴(yán)密·但是，此種方法運算的過程比較麻煩，對抽象思維的要求比較高，計算量較大，因此用此種方法很多同學(xué)還存在一些困難·除了用上面的方法確定數(shù)列項的大小外還可以用什么方法解答？

其次，在函數(shù)圖像上作出數(shù)列的各個點（n，an）；

第三，根據(jù)函數(shù)圖像數(shù)形結(jié)合就可以得到第10項最大，第9項最小·

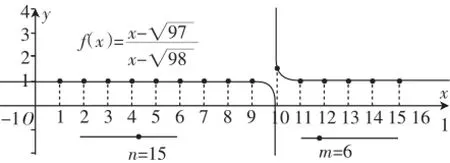
圖3

師：哪位同學(xué)還能提出不同的解題思路？

師：該同學(xué)的思路非常好，此種方法是將an=與過兩點A（x，y），B（x，y）直線的斜率公式k=1122相對比可知，a相當(dāng)于過兩點M（n，n），N（

n）的直線的斜率，因此當(dāng)n變化時，動態(tài)的M點與靜態(tài)的N點形成的線段的斜率的最大值就是要求的an的最大值·從理論上看這種思考方法非常的好，但由于點M（n，n）都在直線y=x上，點N（雖然不在直線y=x上，但是相對的位置非常接近，所以用肉眼很難判定斜率的大小·如圖4所示，即使用計算機作出的圖形也無法判定斜率的不同·由于此題中點的特殊性，因此此題不適合用此方法·但是，如果N點不在M點所在的直線附近，那么此種方法可以采用，并且可以起到一目了然的作用·

圖4

師：從上面三種解題方法看，請一個同學(xué)談一下自己的體會·

生9：解決數(shù)列單調(diào)性問題可以從以下幾方面考慮：

（1）首先想一想從哪些角度可以解決此問題，確定解決此問題的思路或方向·

（2）若從函數(shù)角度解決問題，則需要將數(shù)列問題抽象為函數(shù)問題，利用函數(shù)的圖像和性質(zhì)進行解題·

（3）因為數(shù)列和函數(shù)有很多可以相通的地方，所以數(shù)列問題可以借助函數(shù)進行解題，但數(shù)列并不是函數(shù)，因此要注意二者的區(qū)別·

師：該同學(xué)總結(jié)的非常好·

四、高于教材

師：剛才我們研究了教材上的習(xí)題，同學(xué)們有很多好的解答問題的方法·下面給大家?guī)追昼姷臅r間，請各個小組設(shè)計一個與問題5類似的試題，并說明設(shè)計思路·

生10：我們小組考慮改變兩個常數(shù)為變化的數(shù)值，將問題從特殊變換成一般·

設(shè)計問題1：數(shù)列｛an｝的通項公式是λ∈N+，它的前n項中最大的項是第幾項？最小的項是第幾項？如圖5所示的圖像是我們借助GeoGebra軟件制作的取不同值時的圖像·

圖5

生11：小組2的同學(xué)研究了分式函數(shù)上數(shù)列的單調(diào)性變化情況，常見的函數(shù)當(dāng)然包括二次函數(shù)，因此我們設(shè)計的題目是針對二次函數(shù)進行設(shè)計·

設(shè)計問題2：數(shù)列｛an｝的通項公式是an=n2+2n，n∈N+，它的前n項中最大的項是第幾項？最小的項是第幾項？

師：兩個小組的設(shè)計非常好，能夠?qū)⒊Ｒ姷暮瘮?shù)與數(shù)列進行有機的整合，為數(shù)列單調(diào)性問題的分類提供了依據(jù)·下面結(jié)合該小組同學(xué)的設(shè)想看下面的問題·

五、問題探究

問題6：若數(shù)列｛an｝的通項公式是an=n2+λn，｛an｝是單調(diào)遞增數(shù)列，求實數(shù)λ的取值范圍·

生12：因為數(shù)列｛an｝的通項公式是an=n2+λn，｛an｝是單調(diào)遞增數(shù)列，所以an+1＞an，所以（n+1）2+λ（n+1）＞n2+λn，所以λ＞-（2n+1）·因為-（2n+1）max=-3，所以λ＞-3·

師：該同學(xué)利用遞增數(shù)列的定義建立關(guān)于n、λ的不等式，通過分離系數(shù)得到關(guān)于λ的恒成立不等式，因此λ只需大于-（2n+1）的最大值-3即可·

師：除了上面的解法還可以怎么考慮此問題？

生13：若將an=n2+λn看成關(guān)于二次函數(shù)，則此函數(shù)的圖像是開口向上的拋物線，點（n，an）都是拋物線上的點·如果函數(shù)an=n2+λn的對稱軸n=≤1，即λ≥-2時，根據(jù)二次函數(shù)圖像的特點，都有an+1＞an，此時數(shù)列為遞增數(shù)列·

師：該同學(xué)能夠?qū)n=n2+λn看成關(guān)于n的二次函數(shù)，并利用二次函數(shù)的圖像和性質(zhì)來研究數(shù)列的單調(diào)性，很好地在函數(shù)與數(shù)列之間建立起聯(lián)系的橋梁，體現(xiàn)了數(shù)形結(jié)合思想·但是，考慮到了函數(shù)和圖像間的聯(lián)系，卻忽略了函數(shù)與數(shù)列之間的區(qū)別·數(shù)列是一列特殊的函數(shù)值，因此數(shù)列的單調(diào)性既與函數(shù)的單調(diào)性有聯(lián)系，又與函數(shù)的單調(diào)性有區(qū)別·

（1）如果函數(shù)an=n2+λn的n=1，即λ≥-2時，根據(jù)二次函數(shù)圖像在對稱軸右邊單調(diào)的特點，都有an+1＞an，此時數(shù)列｛an｝為遞增數(shù)列；

所以λ＜-2，且1+λ＜22+2λ，所以-3＜λ＜-2·

綜上（1）（2）所述，實數(shù)λ的取值范圍是λ＞-3·

六、鞏固加深

師：利用上面研究問題的方法解答下面的問題·

問題7：已知數(shù)列｛an｝的通項公式是若｛an｝是單調(diào)遞增數(shù)列，求實數(shù)λ的取值范圍·

生14：因為｛an｝是單調(diào)遞增數(shù)列，所以a以λ＜n（n+1）min=2，所以λ＜2·

師：該同學(xué)的方法思路簡單，根據(jù)數(shù)列單調(diào)性的定義，很容易將數(shù)列遞增的問題轉(zhuǎn)化為不等式恒成立問題，再求參數(shù)的取值范圍·下面請同學(xué)們利用函數(shù)的性質(zhì)進行解答·

n

師：該同學(xué)解答問題的思路很好，能夠?qū)?shù)列和函數(shù)聯(lián)系在一起研究，但是該同學(xué)在思考問題時，人為地將λ的取值范圍進行了縮小，造成解答問題不夠全面的情況·因為實數(shù)λ的取值范圍沒有確定，所以對λ的取值情況要根據(jù)函數(shù)的不同情況進行分類討論，再將各種情況進行合并，找到符合要求的λ的取值范圍·下面請各小組將該問題的解答補充完整·

生16：根據(jù)老師剛才的提示，我們小組認(rèn)為函數(shù)（fx）= x+為對號函數(shù)的條件是λ＞0，所以還要對λ＜0，λ=0兩種不同情況進行思考·我們小組分三種情況進行討論·

（2）當(dāng)λ=0時，an=n為單調(diào)遞增數(shù)列；

圖6

綜上（1）（2）（3）所述，｛an｝是單調(diào)遞增數(shù)列時，實數(shù)λ的取值范圍是λ＜2·

師：該同學(xué)的解法中，首先，將數(shù)列問題和函數(shù)問題結(jié)合在一起，利用函數(shù)思想解決數(shù)列問題；其次，利用分類討論思想將對函數(shù)不同的情況進行了討論；第三，實現(xiàn)了數(shù)列的單調(diào)遞增與不等式組的等價轉(zhuǎn)化·

七、舉一反三

師：通過問題1～問題7的學(xué)習(xí)，復(fù)習(xí)、鞏固、引申了數(shù)列單調(diào)性，對數(shù)列的單調(diào)性有了比較深入的理解·請各小組結(jié)合教材上與單調(diào)性有關(guān)的問題8提出自己小組設(shè)計試題的思路和想法·

（1）求證：an＞-2；

（2）數(shù)列｛an｝是遞增數(shù)列還是遞減數(shù)列？為什么？

師：該小組的同學(xué)能夠利用信息技術(shù)手段研究數(shù)學(xué)問題，開辟了數(shù)學(xué)新的研究方式·數(shù)學(xué)已經(jīng)不僅僅進行邏輯推理得出結(jié)論，數(shù)學(xué)已經(jīng)變成了一個實驗性的學(xué)科，將會有更多的數(shù)學(xué)結(jié)論通過實驗被發(fā)現(xiàn)·此種思路很好，課后請同學(xué)們按照該小組提出的設(shè)計思路命制出符合要求的試題·

生18：我們小組考慮的是問題中給出的是分式函數(shù)，如果在此函數(shù)的基礎(chǔ)上乘以一個x+a，那么函數(shù)將變成k（x）=（x+a）f（x）的形式，整理、換元后該函數(shù)k（x）是關(guān)于x的“對號函數(shù)”形式，并且含有參數(shù)a，這樣就可以設(shè)計出下列問題·

師：該小組同學(xué)從另一角度思考了這一問題，通過一個簡單的變形，將一個問題轉(zhuǎn)化為另一問題，將前面研究的兩個試題整合在一起，這種思考問題的方法可以大大地拓寬試題的設(shè)計思路，命制出更好的試題·

八、課堂小結(jié)

師：下面請各小組對本節(jié)課進行小結(jié)·

生19：復(fù)習(xí)鞏固了數(shù)列單調(diào)性的定義，并能應(yīng)用定義判斷數(shù)列的單調(diào)性·

生20：能夠?qū)?shù)列的單調(diào)性與函數(shù)的單調(diào)性進行整合，借助函數(shù)的單調(diào)性研究數(shù)列的單調(diào)性·

生21：利用信息化手段可以進行數(shù)學(xué)試驗獲得數(shù)學(xué)結(jié)論，探索獲取新知識、新結(jié)論的方法·

生22：通過舉一反三環(huán)節(jié)可以有效地培養(yǎng)創(chuàng)新意識和創(chuàng)新能力·

九、反思啟發(fā)

什么樣的課是好課？不同的人對好課的理解會有所不同·比如：華東師范大學(xué)教授葉瀾認(rèn)為：一堂好課沒有絕對的標(biāo)準(zhǔn)，但有一些基本的要求·

（1）有意義：學(xué)生的學(xué)習(xí)首先是有意義的·初步的意義是他學(xué)到了新的知識；進一步是鍛煉了他的能力；往前發(fā)展是在這個過程中有良好的、積極的情感體驗，產(chǎn)生進一步學(xué)習(xí)的強烈要求；再發(fā)展一步，是他越來越會主動投入到學(xué)習(xí)中去·對于高三復(fù)習(xí)來說問題的選取要源于教材、高于教材，要將高考的要求與教材上的例題、習(xí)題有機地結(jié)合在一起·在本節(jié)課中幾個試題的原型都來自于教材，因此從有意義的角度看，完全符合要求·

（2）有效率：一是對面上而言，這節(jié)課下來，對全班學(xué)生中的多少學(xué)生是有效的，包括好的、中間的、困難的，他們有多少效率；二是效率的高低·有的高一些，有的低一些，但如果沒有效率或者只是對少數(shù)學(xué)生有效率，那么這節(jié)課都不能算是比較好的課·從這個意義上講，這節(jié)課應(yīng)該是充實的課·整個學(xué)習(xí)過程，有課前的復(fù)習(xí)總結(jié)、有課上的展示發(fā)言、有問題的拓展引申、有課后的完善，課上、課下大家都有事情干，通過教師的點評，學(xué)生都能從中獲得啟迪，整個課堂的容量很大·

（3）生成性：本節(jié)課不完全是預(yù)先設(shè)計好的，而是在課堂中有教師和學(xué)生真實的、情感的、智慧的、思維和能力的投入，有互動的過程，氣氛相當(dāng)活躍·在本節(jié)課中，既有資源的生成，又有過程狀態(tài)的生成，既研究試題本身的變化，又研究試題所反映出的本質(zhì)特點，學(xué)會對試題進行歸類，這樣的課可稱為豐實的課·

（4）常態(tài)性：平時的教學(xué)離不開教材，善于對教材上的試題進行總結(jié)、分類、合并、變形是教學(xué)的常態(tài)，本節(jié)課就很好地反映了這一點·

（5）有待完善：本節(jié)課還有需要完善的地方，特別是在短時間內(nèi)研究了這么多的問題，即使學(xué)生課前有所研究，但時間上還是顯得比較緊張·只要是真實的課就會有缺憾，課不能十全十美，十全十美的課造假的可能性最大，有缺憾是真實的一個指標(biāo)，筆者喜歡上這樣的課·生活中的課本來就是有待完善，這樣的課稱之為真實的課·扎實、充實、平實、真實，說起來好像很容易，真正做起來卻很難，但正是在這樣的一個追求過程中，教師的專業(yè)水平才能提高，心胸才能博大起來，同時也才能真正享受到：“教學(xué)的過程是一個創(chuàng)造性的過程，也是歡樂和智慧的體驗過程”·F