一道定值問題的另解、背景及變形

☉江蘇省如皋市薛窯中學夏俊梅

一道定值問題的另解、背景及變形

☉江蘇省如皋市薛窯中學夏俊梅

《數學通報》2009年第3期刊出的問題1783（以下簡稱題1）是：設M是定圓O外一個定點，試問：在定圓O內是否存在一個定點N，使得對于定圓O上的任意點P，比值為定值？若存在，求出該定點N；若不存在，請說明理由·

筆者覓得此題不同于供題者的另一種解法，這種解法與供題者的解法相比，顯得較為笨拙，但這種解法卻能揭示定點N的一個有趣性質·當然，該題也有古老的歷史背景，從而我們可變形出許多與該題同樣精彩的其他問題·

一、另解

首先證明一個命題·

命題：設M（m，0）是不在圓O：x2+y2=a2上且不與O重合的一個定點，過M作不與x軸垂直的一動直線與圓O交于兩點A、B，取A關于x軸的對稱點C，則直線BC必過定

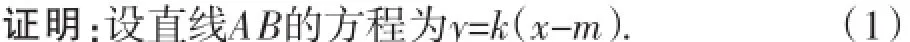
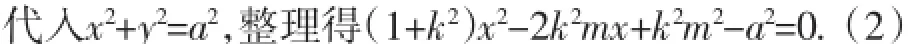
設A（x1，y1）、B（x2，y2），則由（2）得：

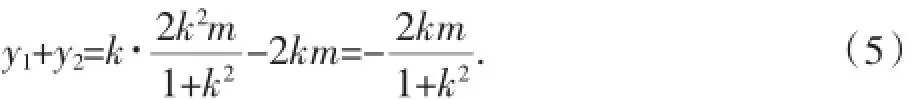
同樣由（1）可知：x1y2+x2y1=x1［k（x2-m）］+x2［k（x1-m）］=2kx1x2-km（x1+x2）·

由（1）可知y1+y2=k（x1+x2）-2km，將（3）代入，得：

再將（3）、（4）代入上式，得x1y2+x2y1=2k·

由題意得直線BC的方程為：

現在解題1·

解：過M、O兩點作直線與圓O交于A、B兩點，如圖所示·過M作圓O的一條切線，切點為P′·然后過P′作MO的垂線，垂足為N，則定點N即為所求·

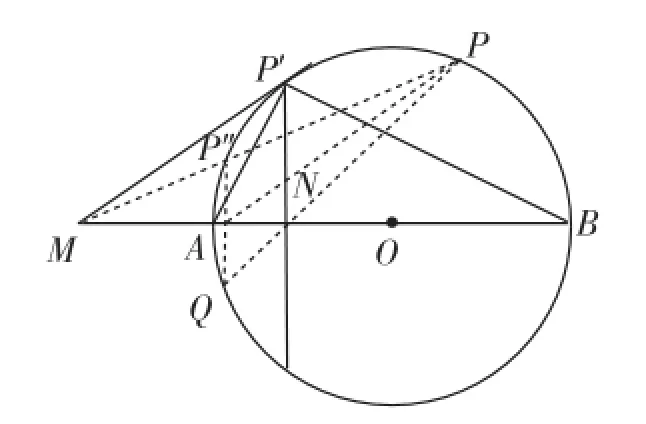
連接P′A，則P′A為∠MP′N的平分線·

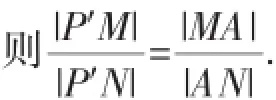
連接P′B，則P′B是△P′MN的外角平分線，也有：

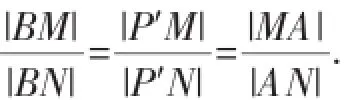
過M作圓O的任一條不與AB重合的割線MP′′P，如圖，作P′′關于直線AB的對稱點Q，連接PQ、PA，則由命題PQ必過直線AB上一定點N′，N′必滿足|ON′|·|OM|=|OA|2，而N點滿足|ON|·|OM|=|OA|2，則N與N′重合·

至此，我們得到求N點的不同于供題者的另一種解法·這種方法比供題者的方法易于操作·另外，我們還獲得N點如命題揭示的一個性質·

二、背景

歷史上有這樣一道題：設一動點至兩定點的距離之比是一個不為零的常數，求這個動點的軌跡·

此題以下簡稱題2，見文1·

若常數為1，則動點的軌跡是以兩定點為端點的線段的垂直平分線；若常數不為1，則取這兩定點關于此比值的內比分點及外比分點，再以這兩點為直徑作圓，符合條件的動點的軌跡就是這個圓·

這個圓叫做阿波羅尼斯（Apollonius，約公元前260～200年）圓·

供題者提供的解答也并非“原創”，與文1中題2的解答完全相同·

若我們利用阿波羅尼斯圓的性質，則題1的解答更為簡潔·

知道了題1的背景，我們可讓M更“自由”一些，不一定在圓O外部，M在圓O內部且不與O重合，也有類似結論，故題1可改為題1′·

題1′：設M是不在定圓O上，也不與O點重合的一個定點·試問：是否存在一個定點N，使得對于定圓O上的任意點P，比定值？若存在，求出該定點N；若不存在，請說明理由·

這樣找N點要分兩種情形·若M在圓O外部，上文已給出找N點的方法；若M在圓O內部，作MP′⊥MO與圓O交于P′，過P′作圓O的切線，與直線MO交于N點，則點N為所求·以下解法與上文提供的方法無異·

如果按射影幾何的理論，題1及題1′實質上是已知三點，求第四點，使這四點成調和比·故題1及題1′有如下簡解·

連接MO與圓O交于A、B，則使（AB，MN）=1的N點即為所求·

三、變形

有了上文的準備，我們可隨心所欲地對題1進行改編、變形·

題3：設A、B為兩個定點，D是線段AB上不與端點重合的一個定點，求動點C的軌跡，使CD恒為△CAB的內角C的平分線·

題4：設A、B為兩個定點，D為線段AB的延長線上一個定點，求動點C的軌跡，使CD恒為△CAB的內角C的外角平分線·

題5：設直線l是經過定圓圓心的一條直線，試問：在直線l上能否找到兩個定點M、N，使得對于定圓上的任意一點P，恒有比值2？若存在，求出這兩個定點M、 N；若不存在，請說明理由·

題6：設直線l是經過定圓圓心的一條定直線，試問：在直線l上能否找到兩個定點M、N，使得對于定圓上任一點P，恒有=k（k為常數）？若存在，求出這兩個定點M、N；若不存在，請說明理由·

題7：設直線l是與定橢圓的長軸重合的一條直線，試問：在直線l上能否找到兩個定點M、N，使得對于定橢圓上的任一點P，恒有=k（k為常數）？若存在，求出這兩個定點M、N；若不存在，請說明理由·

題8：M是圓O外一點，線段MO與圓O交于一點P，過M作圓O一條不過圓心的割線，與圓O交于A、B，AC⊥MO，與圓O交于另一點C，BC與MO交于N，設D是圓O上不與MO共線的一點·求證：DP是∠MDN的平分線·

1·梁紹鴻·初等幾何［M］·北京：人民教育出版社，1980·A