把握題目特征思路順利生成
——以三角函數問題為例說明

☉江蘇省啟東中學蔡罡

把握題目特征思路順利生成
——以三角函數問題為例說明

☉江蘇省啟東中學蔡罡

在數學教學中部分學生常存在“一聽就懂，一過就忘，一做就錯”的現象·造成這種現象的一個主要原因是老師在講解題目時忽視對學生審題能力的培養，導致學生在審題時快慢速度掌握不好，不能抓住題目的“題眼”·因此老師要講授的應該是審題突破口的尋找，自己是怎么找的，這種想法和思維過程要暴露在學生面前，讓學生自己體會如何尋找“題眼”·本文以三角函數問題的求解中，解題思路的尋找為例，談幾點看法，供同學們參考·

一、準確詮釋條件，探尋解題思路

問題的解答都是從審題入手的，條件的審視是否全面、準確是題目能否順利求解的關鍵·考題中每一個字都不是多余的，審題中尤其要注意一些重要的關鍵字眼，如題目給了哪些條件，由這些條件可直接或間接得出哪些有用的信息·條件與所求結論有哪些關系？如何將條件與結論進行合理轉化，轉化即可以是將條件化為結論，也可以將結論化為條件等·

評析：思路的生成并不是憑空產生的，題目的求解是否順利，源于審題，題干中包含了解題所需要的全部信息，解題中如果發現某個條件沒有用到，或者感覺缺少條件，那就需要對問題進行重新審視了·

二、深挖隱含條件，變不定為確定

由于近幾年教學大綱對三角函數的要求在難度上有所降低，從而這一類型的試題難度不會太大·但是由于三角函數的內容繁雜，在三角解題中，公式較多且性質靈活，隱含條件多，導致部分同學顧東不顧西，故解題時稍有不慎，常會出現漏解、增解、錯解現象，其根本原因是對題設中的隱含條件挖掘不夠·因此，分析研究題目中隱含的條件就顯得很重要·

例2如果存在正整數ω和實數φ使得函數f（x）= cos2（ωx+φ）（ω，φ為常數）的圖像如圖1所示（圖像經過點（1，0）），那么ω的值為（）·

A．1B．2C．3D.4

圖1

圖2

思路生成：圖形是題目所給的重要信息之一，因此把握圖形的結構特征是問題突破的關鍵·如圖2，易知

又f（x）=cos2（ωx+φ）=

評析：高考解答題中根據圖像求函數的解析式，關鍵是能根據題目中信息準確獲得周期、振幅及初相這三個要素·比如兩個相鄰的對稱軸之間的距離就是半個周期·又如某三角函數圖像至少平移m（m＞0）個單位后與原圖像重合，也就意味著函數的最小正周期為T=m，準確識圖，巧妙用圖是本題求解的關鍵·

三、將問題進行等價轉化，化生為熟

數學問題求解的過程其實就是轉化的過程，即將復雜的問題簡單化，陌生問題熟悉化等，利用我們所熟悉的問題來求解陌生的問題，是常用的解題思維之一·例3已知函數（fx）=sin，任取t∈R，定義集合：At=｛y|y=（fx），點P（t，（ft）），Q（x，（fx））滿足|PQ|≤｝·設Mt，mt分別表示集合At中元素的最大值和最小值，記· h（t）=Mt-mt，則（1）函數h（t）的最大值是_______；（2）函數h（t）的單調遞增區間為_______·

解析：At=｛y|y=f（x）｝，點P（t，f（t）），Q（x，f（x））滿足|PQ|≤為半徑的圓及其內部函數f（x）=

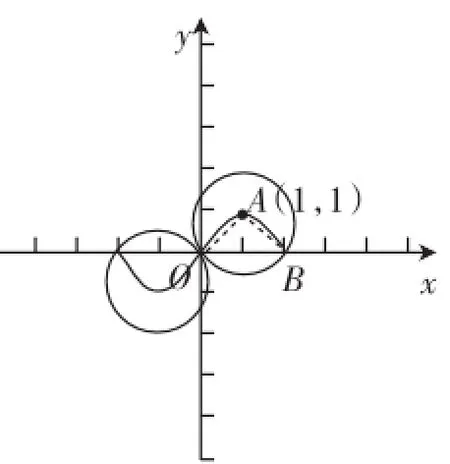
圖3

坐標的集合，如圖3所示·

因為f（-2）=f（0）=0，f（1）= 1，（f-1）=-1，設A高點Q的橫坐標·

所以函數h（t）的最大值是2（t=4k或t=4k+2時取得）·

單調增區間為（2k-1，2k），k∈Z·

評析：化歸轉化思想是數學中最基本的思想方法之一，化歸轉化思想解題的途徑是靈活多變的，通過化歸轉化，達到由陌生到熟悉、復雜到簡單、困難到容易的轉化·對于本題的解答，有效地將條件At=｛y|y=f（x），點P（t，f（t）），Q（x，f（x））滿足|PQ|≤｝進行等價轉化，即轉化為“以點P為圓心，為半徑的圓及其內部函數f（x）=圖像上所有點的縱坐標的集合”是問題求解的關鍵，并利用正弦函數的周期性、單調性與最值可求得Mt，mt，從而求得函數h（t）=Mt-mt的最大值·

四、注重解題反思，有效避錯

有些問題，就思路而言，并沒有錯，但學生的認知能力有差距，教師要基于學生的認知水平，找到適合學生思維能力的認知途徑·正如美國認知教育心理學家奧蘇貝爾所言，當學生把教學內容與自己的認知結構聯系起來時，意義學習便產生了·學習實質是新舊知識相互作用并建立聯系的過程，教師的教學最基本的工作就是使新知識與學生頭腦中的知識、經驗、方法建立實質性聯系·

反思：本題的求解學生易想到：利用sin2α+cos2α=1與已知條件組成方程組，求出sinα，cosα，從而求出tanα·

這種方法最易想到，理論上都能解出，但對有些系數復雜的方程組解起來有一定的難度·本題把方程組化為一元二次方程后，出現了無理系數，就不知如何解了·能不能避免這種復雜計算呢？

評析：在課堂上，教師要鼓勵學生把自己的思維過程用語言表達出來，進而判斷這種方法是否可行，是不是順暢，同時與其他解法比較，哪種更易想到，更簡捷，哪種方法更具有通性·通過語言表達充分反應出解題過程中是否有“跳步”“漏步”現象，從而增強學生思維的嚴密性·

課堂是教師培養學生的主要陣地·學生在課堂上要有所得，主要的不是教師直接告知，而是通過學生自己的主動參與，自主探索，教師引導解題思路的產生，從而達到對知識的掌握，思想方法的領悟·在數學的天地里，重要的不是知道什么，而是我們是怎么知道的，而這個怎么知道的過程正是課堂中最重要的東西——生成·F