一類最值問題的探究與思考
☉浙江省鄞州區正始中學張朱艷
一類最值問題的探究與思考
☉浙江省鄞州區正始中學張朱艷
最值問題是高考數學的常見題型和重要考點·用導數來解決最值問題,是我們熟悉而又常用的方法·但從2015年起,導數退出浙江高考數學的舞臺,只在自選模塊中考查,這嚴重阻礙了高考中最值問題的求解·因此,一類不用導數解決的最值問題,應該引起我們的足夠重視·

初次見到本題時,學生普遍感覺難度大,無從下手·
其實,在2011年,我們已經接觸過非常類似的題目:(2011年高考浙江理科)設x、y為實數,若4x2+y2+xy=1,則2x+y的最大值是_________·
可為什么學生又不會呢?
對于此類最值問題,我們又如何做到舉一反三、觸類旁通呢?
下面以2011年高考浙江理科的這道題為例,談談如何解決這類最值問題·
一、鼓勵多解
學生解題時常會按習慣了的單一思路去思考數學問題,高三復習中要鼓勵、引導學生從多側面、多角度思考問題,挖掘問題的實質·

解法2:利用函數思想·
(2x+y)2=4x2+y2+4xy=1+3xy,所以要求2x+y的取值范圍,只需求出xy的取值范圍·

二、引導多悟
做完試題要及時進行總結反思,因為解題的價值不是答案本身,而在于弄清“問題的本質是什么?”“是怎樣想到這個解法的?”“是什么促使你這樣想、這樣做的?”,這就是說,解題過程還是一個思維過程,是一個把知識與問題聯系起來思考、分析、探索的過程·
顯然由本題的條件4x2+y2+xy=1,知4x2+xy+y2-1=0.
Δ=12-4×4×1=-15<0·
所以方程4x2+y2+xy=1所表示的曲線為橢圓,本題的本質為橢圓4x2+y2+xy=1與動直線t=2x+y有公共點,求t的最大值·顯然當直線與橢圓相切時,t取得最大值
一道數學試題能否解得順利,富有創意,甚至正確與否,常常取決于能否發現和利用好題目中的潛在信息·那么潛在信息潛在哪里?又該如何挖掘與利用呢?一般地,(1)信息潛在題設的條件中;(2)信息潛在題設的結構中;(3)信息潛在問題的背景中;(4)信息潛在所求的結論中·
解法1因為發現這是兩個變量的和與積關系的最值問題,所以想到了利用重要不等式;解法2因為發現條件和結論中有平方關系,所以想到了利用函數思想;解法3因為發現兩個變量問題求最值關鍵是減少變量,所以想到了利用參數方程;解法4因為發現只是研究與“二次”有關的不等問題,所以想到了“Δ”·
于是,我們不難得出引題的解法·(略)
一題多解的目的是通過思想方法的逐一呈現,從學生最易上手的方式、方法入手,逐步逐級給予引導和批判,不畏艱難,不斷優化解題思維品質,從而最終達到提升自身解題的能力·
三、學會多變
在保持問題的本質不變的條件下,適當地改變試題的條件和結論進行變式,利于學生由淺入深地研究問題,利于學生感悟試題考查的知識點,體驗數學的本質,徹底地從題海中走出來,從而減輕學生負擔,提高學習效率·
基于2011年這道高考題的本質是:圓錐曲線與直線有公共點,求動直線在y軸上的截距,有以下變式·
變式1:設x、y為實數,若4x2+y2+xy≤1,則2x+y的取值范是圍是_________·

本題的本質是動直線與橢圓所包含的區域有公共點,求參數t的取值范圍·
變式2:設x、y為實數,若x2+4xy+y2=1,則2x+y的取值范圍是_________·

本題的本質是動直線與雙曲線有公共點,求參數t的取值范圍·
變式3:設x、y為實數,若x2-4xy+4y2+x+y=1,則2x+y的取值范圍是_________·
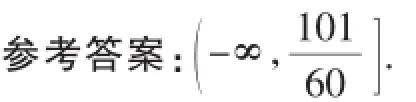
本題的本質是動直線與拋物線有公共點,求參數t的取值范圍·
參考答案:[1,+∞)·
變式5:設m、x、y為實數,滿足mx+y=5,且4x2+y2+ mxy=1,則m的取值范圍是_________·

本題的本質是二次曲線與動直線有公共點,求直線方程與二次曲線方程所對應的參數的取值范圍·
基于2011年這道高考題的實施方法是:運用重要不等式,有以下變式·
變式6:設x、y為正實數,若2x+y+6=xy,則xy的最小值是_________·
參考答案:18·
變式7:設x、y為正實數,若x+2y+2xy=8,則x+2y的最小值是_________·
參考答案:4·
變式8:設x、y為正實數,若x+3y=5xy,則3x+4y的最小值是_________·
參考答案:5·
對于這一類最值問題的解決,一般有以上幾種解法與變式·
同時,我們看到:解題教學的目的是為了培養學生從多角度分析問題,用多途徑解決問題的能力;解題教學不能“太匆匆”,對于某些數學問題,教師要通過簡明審題來把問題尋解的過程暴露給學生,使學生既“知其然”又“知其所以然”,使學生在遇到相關問題時,能迅速找到解題的突破口·
1·黃加衛·構造性解題方法的幾點注記[J]·數學教學研究,2005(11)·
2·劉丹·波利亞數學教育思想對我國數學教育改革的啟示[J]·理工高教研究,2003(6)·
3·康武·波利亞與數學教育[J]·中學數學教學參考,1998(5)·A

