用MatheGS系統輔助高等數學教學的一點探索

陳麗紅 方文波

摘 要：通過分析當前高等數學教學時所面對的教育信息化現狀，PPT課件輔助高等數學教學時的優勢以及一些不足，采用高等數學圖形系統（MathGS）進行高等數學教學的一些嘗試，突出多媒體的交互性功能，增強課件制作的實效性，把現代教育技術引入到高等數學教學中，教師可以借助現代教育技術搜集、加工、處理和傳遞高等數學教學信息，讓學生感受到和體會到現代教育技術在高等數學中的優勢。

關鍵詞：高等數學 高等數學圖形系統（MathGS） 教學教育信息化

中圖分類號：G642 文獻標識碼：A 文章編號：1674-098X（2015）02（a）-0125-02

隨著信息技術的飛速發展，教育信息化在世界范圍內已受到各國政府的高度重視。我國政府于2010年7月正式發布了《國家中長期教育改革和發展規劃綱要（2010—2020年）》[1]，教育部于2012年3月正式發布了《教育信息化十年發展規劃（2010—2020年）》。在這兩個綱領性文件中明確指出：加快教育信息基礎設施的建設，把教育信息化納入國家信息化發展的整體戰略，基本建成覆蓋城鄉各級各類學校的數字化教育服務體系，促進教育內容，教學手段和方法的現代化[2]。

在高等學校中，高等數學是理工科、財經類等專業的一門重要基礎課，它對培養學生的抽象思維能力、邏輯推理能力、空間想象能力和科學計算能力等都可以起到很大的幫助，這一點是其他課程無法替代的。而這門課學習的好壞直接關系到后續專業課程的學習。因此，如何讓學生更加有效的學習高等數學，使學生可以靈活的運用數學知識、數學思維解決實際問題是大學數學教育工作者一直以來追求的目標。

以現代教育技術為主導的現代教育技術觀應該是全方位的，重視硬件建設的同時也應該重視軟件建設。信息技術和網絡技術的飛速發展，為高等數學的教學帶來了極大的活力[3]。由于信息資源日益突出的重要性，高等數學這門課程也不再是預先規定好的凝固不變的知識結構，而是不斷變動，不斷更新的教育媒體，把整個教學過程應看作是一個信息系統在運作。現代教育技術引入到高等數學教學中，高等數學授課教師可以借助現代教育技術搜集、加工、處理和傳遞高等數學教學信息，學生可以借助現代教育技術查詢、探索、接受和加工高等數學教學信息，高等數學授課教師要讓學生感受到和體會到現代教育技術在高等數學中的優勢。同時，也讓學生逐漸熟悉和掌握現代教育技術環境下的新型學習模式和學習方法。學生所要學習的高等數學不僅僅是以課本為載體的信息，聲音、圖像等多元化的信息也作為教學內容引入到高等數學課堂教學中[4]。

在高等數學中，空間解析幾何是學生最不容易理解的知識之一。很多學生缺乏空間想象能力，對課本上的空間解析幾何圖形理解差，對于常用的柱面、旋轉面及二次曲面的圖形特點掌握不好，而這些知識的熟練掌握對學好后面的多元函數微分學與積分學等知識是必不可少的。目前許多講授高等數學的老師在講這一章時大多采用黑板、粉筆加上PPT課件教學，這樣可以通過一些圖形或者動畫使學生理解起來較為容易。但是PPT的動畫制作需要花費老師的大量時間，大多數只是單向演示型，教師只能播放事先做好的圖片或動畫，不可能把所有圖形都準備好，即使都做好了，也不可能都在課堂上演示，而且對于學生理解或不理解的內容不太好選擇，最關鍵的是做好之后在課堂上不能隨著教學需要實時更改，比如說函數發生了變化，圖形應該相應發生變化等等之類。由于這些都是事先做好而不能及時了解學生的需求，因而難以滿足師生互動或人機互動的教學要求。有些老師用MATLAB或CAJ畫圖來解決這一問題，但并不是每個教授高等數學的老師都會使用MATLAB或CAJ這些軟件，因此不具有全面性。

我們這里在處理這些內容時采用方文波老師研制的高等數學圖形系統（MatheGS）輔助教學，力圖使同學們在學習這一些內容時能夠覺得生動形象。高等數學圖形系統不需安裝，可直接在Windows下運行；系統小巧，可拷入U盤，攜帶方便；使用簡單，不需編程，用戶只需具備高中及以上的數學知識和掌握基本的Windows操作即能使用；能繪制任何曲線（包括顯式曲線和隱式曲線）和曲面（包括顯式曲面和隱式曲面）；用戶在繪圖時，系統提供了兩種函數確定模式：選擇函數和輸入函數；在選擇函數模式中，將常見的曲線和曲面的方程內植在系統中，用戶只需單擊這些函數方程即可實現繪圖，以節省時間。在輸入函數模式中，用戶可自行輸入函數進行繪圖。現在以旋轉曲面為例具體說明一下。

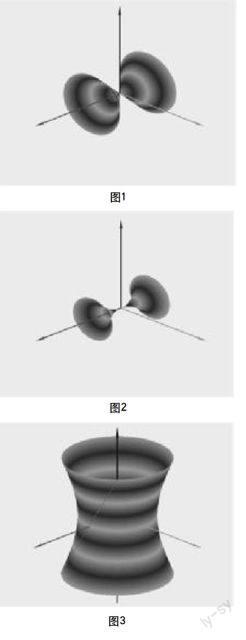
比如說我們要畫一個圓錐面就可以在選擇函數里首先選擇直線方程然后確定參數繞x軸旋轉繪圖，選擇動畫出現圖1效果圖。

如果學生覺得圓錐面太簡單，可以考慮再換一個稍微復雜一點的旋轉曲面如旋轉拋物面，在選擇函數里選擇方程確定參數繞x軸旋轉繪圖，選擇動畫出現圖2效果圖。

對于單葉雙曲面這個圖形從旋轉曲面的角度來看，學生還很容易接受。但大多同學不理解為什么單葉雙曲面會是一個直紋面，以及雙曲拋物面也是一個直紋面？這個可以在課堂上直接用高等數學圖形系統給學生演示，讓他們直觀的看見一條直線繞另一條直線旋轉也可以得到單葉雙曲面。如圖3所示。

運用高等數學圖形系統（MatheGS）系統，可以在課堂上隨時修改參數的值，觀察圖形的變化，起到一種立竿見影的效果。還可以根據教學需要更改函數，觀察不同的曲線所形成的曲面，直觀、具體，使學生更加容易掌握這一類知識。

在高等數學中函數展開成冪級數也是學生不容易理解的內容之一，特別是當函數滿足一定條件時可以用多項式逼近函數，這個可以直接用定理來計算，但怎么會是這樣的結論學生無法直接理解。這時我們可以用高等數學圖形系統（MatheGS）里面的函數逼近來直觀的展示一下逼近的效果。可以從低階多項式逼近，到高階多項式逼近，具體多少階多項式逼近可以在課堂上即刻選擇，作圖，讓學生觀察在逼近過程中圖形的變化，更形象、生動，從而達到學生理解并牢固掌握這一內容的目的。

在高等數學中，對教師來講把積分的定義用分割、近似、求和、取極限這幾步來做講清楚還是有些難度的，用高等數學圖形系統（MatheGS）輔助講解將有助于學生更好地理解這一部分內容。例如用里面的求曲邊梯形的面積來闡述定積分的定義，可以通過任意加大分割的次數來讓學生理解：為什么分割越細矩形面積越接近曲邊梯形的面積，可以更好地理解取極限的意義。

最后這個系統對電腦，對老師沒有多的附加要求，只要是教授高等數學的老師都可以直接運用。我們這里只是借助幾個例子來說明一下在《高等數學》這一門課的教學中可以更廣泛的采用多種信息手段以達到讓學生掌握知識點的目的。

參考文獻

[1] 《國家中長期教育改革和發展規劃綱要（2010—2020年）》[Z].

[2] 《教育信息化十年發展規劃（2010—2020年）》[Z].

[3] 張穎，吳建華.高等數學多媒體輔助教學的實踐與思考[J].高等數學研究，2006，9（4）：111-112.

[4] 嚴露.關于大學高等數學教學改革的探討[J].現代閱讀，2012（9）：19.

[5] 杜彥娟.高等數學課堂自主探究式教學模式的研究[J].煤炭技術，2013，32（1）：255-256.

[6] 李銘洋，曹萍萍.MATLAB在高等數學實驗中的應用[J].沈陽農業大學學報：社會科學版，2009，11（6）：722-725.