相空間重構延遲時間互信息改進算法研究

蔣愛華，周璞，章藝，華宏星

(1.中國船舶重工集團公司第704研究所減振中心，上海 200031;2.上海交通大學機械系統振動國家重點實驗室，上海 200240)

相空間重構延遲時間互信息改進算法研究

蔣愛華1，2，周璞1，章藝1，華宏星2

(1.中國船舶重工集團公司第704研究所減振中心，上海 200031;2.上海交通大學機械系統振動國家重點實驗室，上海 200240)

針對改進互信息算法利于快速可靠獲得時間序列相空間重構的延遲時間問題，通過等邊緣分布2、4等分Lorenz時間序列構成平面分析Cellucci互信息算法缺陷;用大小順序值代替原序列數值、判斷新序列數值所在等邊緣概率區間獲得概率分布矩陣、修正概率分布矩陣最末行與列改進Cellucci互信息算法;以改進算法所得最佳延遲時間進行Lorenz時間序列相空間重構并以小數據量法得出其最大Lyapunov指數，對比雅可比矩陣法所得最大Lyapunov指數以確認改進算法的有效性。結果表明，時間序列長度不能整除劃分區間數時Cellucci互信息算法會獲得錯誤的最佳延遲時間;所提改進算法能消除Cellucci算法缺陷，且計算速度快于Fraser算法;數據序列長度較大時改進算法結果更穩定;由兩種最大Lyapunov指數計算方法所得結果間誤差較小，表明改進的互信息算法有效、可靠。

相空間重構;延遲時間;互信息;Cellucci算法;最大Lyapunov指數

對測試所得振動信號時間序列進行相空間重構，可在不清楚振動系統結構與影響參數時研究振動系統特性。因此在非線性振動系統分析中獲得一定應用［1－2］。

互信息算法為相空間重構中確定延遲時間的常用方法。設{s(ti)}(i=1，2…N)為試驗觀測所得時間間隔為△t的一維性時間序列，該序列可重構為

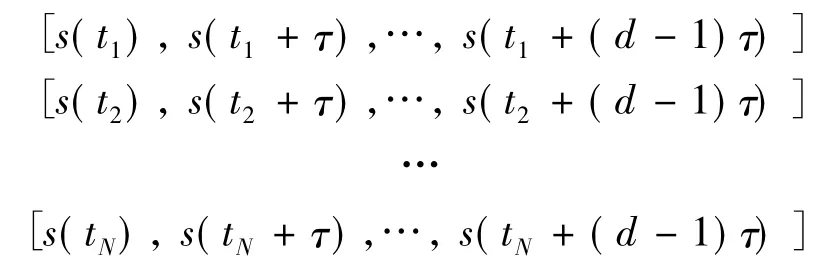
式中:τ為延遲時間。

式中:H(Q)，H(S)，H(Q，S)分別為Q、S的信息熵及Q與S間互信息熵，通常以第一個互信息極小值點所在位置作為最佳延遲時間。

在計算兩時間序列間互信息時常將兩時間序列S與Q值對應到兩相互垂直軸上，構造成SQ平面;并將每個序列中最大與最小值間區域按一定準則分別劃分為若干區間si，qj，則該兩序列數據對將對應于SQ平面中點。通過計算區間si中數據對點數，除以總數據對數N則可得各區間邊緣分布概率。兩時間序列區間相互重合區域為(si，qj)，計算該區域內數據對點數并除以總點數，則得重合區域內聯合概率密度，從而可得S，Q序列間互信息。H(Q)，H(S)，H(Q，S)表達式為

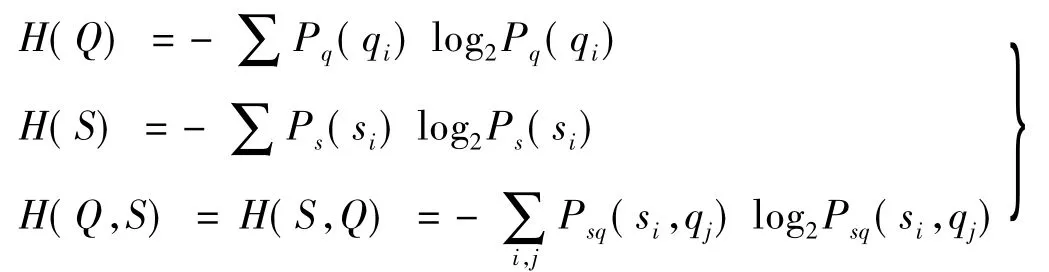
式中:Pq(qi)，Ps(si)，Psq(si，qj)分別為Q在qi區域的邊緣分布概率密度、S在si區域的邊緣分布概率密度及S與Q在(si，qi)區域的聯合概率密度。

SQ平面劃分示意圖見圖1。Q，S間互信息化簡為

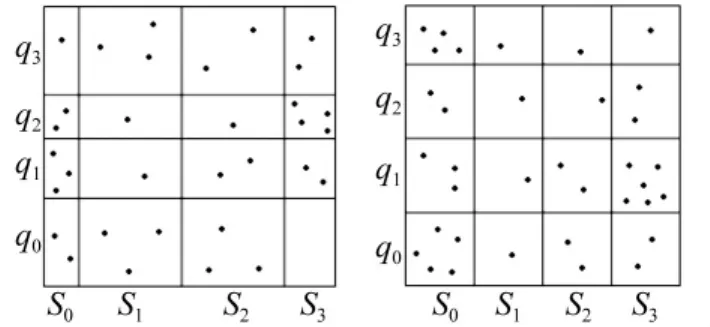
圖1 SQ平面劃分示意圖Fig.1 Skeleton map of SQ plane partition

1 互信息算法

1.1 SQ平面劃分準則

劃分SQ平面準則主要有等邊緣概率分布與等間距兩種(圖1)。等邊緣概率分布劃分區間即使劃分后區間具有相同數據對點數。第一個用互信息法確定最佳延遲時間Fraser算法即采用該方法［3］。Fraser算法按等邊緣分布將SQ平面劃分為4個網格，判斷每個網格是否存在子結構或已稀疏。若無子結構或已稀疏則無需細分，若存在子結構則據邊緣概率對含子結構區域進行等邊緣分布劃分，直到各區域內無子結構存在。判斷是否存在子結構準則為數據對是否均勻分布于區域內。Fraser算法示意圖見圖2。由圖2看出，區域R1(2)、R1(3)中數據點均勻分布無需進一步劃分;區域R1(1)、R1(4)、R2(4，2)中存在子結構，則需進一步劃分。

因此，Fraser算法計算互信息時子結構網格數按4的冪次方增加，且為確定子結構是否存在需將各區域按等邊緣概率分布劃分兩層，判斷各下層子結構網格中的數據點數。計算過程中需存儲各層子結構概率分布，故Fraser算法耗時、耗空間。

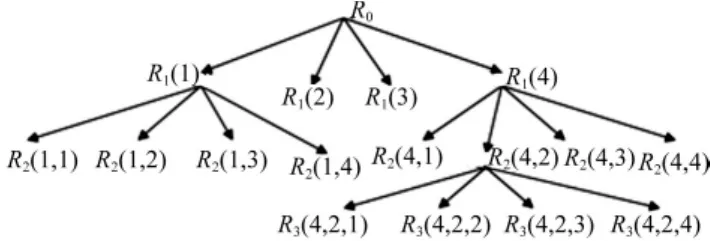
圖2 Fraser－Swinney算法示意圖Fig.2 Skeleton map of Fraser－Swinney algorithm

等間距劃分區間可使各劃分區間距上下限差值相同。與Fraser算法相比該方法計算速度較且程序編譯簡單，但存在互信息對劃分區間數極敏感，即劃分區間太多則會有大量區域內數據點數為0或1，無法反映數據對的概率分布，并獲得錯的互信息。反之，若劃分區間太少則各區域內存在子結構而獲得互信息值不準確。此外，該方法所得結果不適用于對不同變量的時間序列需相同等間距劃分區間數的多變量非線性時間序列重構。

圖3 Rossler微分方程中三變量時間序列等間距劃分下求互信息Fig.3 Mutual information of time series from the three variables ofRossler with equal－distance elements

以Rossler數值大小分布不均時間序列為例，采用相同等區間劃分數劃分三變量的時間序列，會得到錯誤的最佳延遲時間。圖3(a)為運用四階龍格－庫塔所得10000點Rossler離散序列三維圖，起始點為(－1，0，1)，時間步長為0.05。圖3(b)、(c)分別為Rossler離散序列中三變量的數值分布柱狀圖、等間距40等分數值區間時延遲點數1～200的互信息值圖。可見由變量Z時間序列所得最佳延遲時間不準確。

Rossler方程為

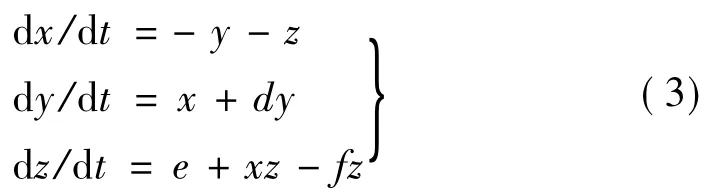
式中:d=0.2，e=0.4，f=5.7均為系數。

大量研究集中于等間距劃分區間數確定。對總長度為N的序列，Mosteller等［4］提出劃分個區間，Bendat等［5］提出劃分1.87(n－1)0.4個區間，Rissanen［6］由算法的隨機復雜性通過對劃分區間進行理論推導認為，擁有最小隨機復雜性的劃分區間數即為最佳劃分區間。隨機復雜性公式為

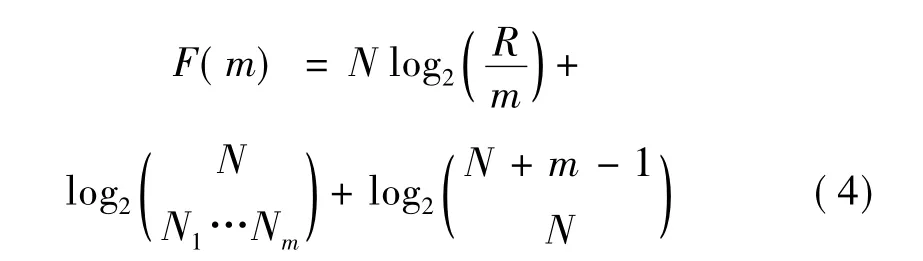
式中:F(m)為隨機復雜性，m為劃分區間數;R為序列中最大最小值之差值;Ni(i=1，2…)為劃分后各區間數據點數，即

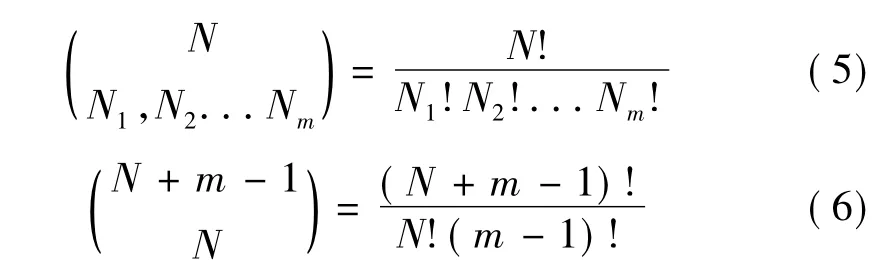
由于N一般較大，式(5)、(6)中存在大數階乘會在計算中溢出，故將式(4)后兩項變換為

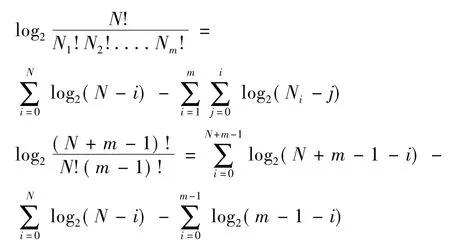
由于復雜度本身的計算為耗時耗空間過程，從而可抵消等間距劃分節約時間與空間優點，目前尚無較好方法用于確定最佳等間距劃分區間數。Cellucci等［7］提出的基于統計的等邊緣劃分區間互信息算法，不僅能滿足多變量時間序列重構要求，且計算速度更快。

1.2 Cellucci互信息算法

互信息算法［7］建立于兩序列S，Q間統計獨立假設，此時S，Q形成的數據點會在SQ平面均勻分布(圖1)，由式(2)知S，Q間互信息將為零。此時SQ平面內任意區域點數為已知，設S軸第i區間內點數為OS(i)，Q軸第j區間內點數為OQ(i)，則區域(i，j)內點數ESQ(i，j)為

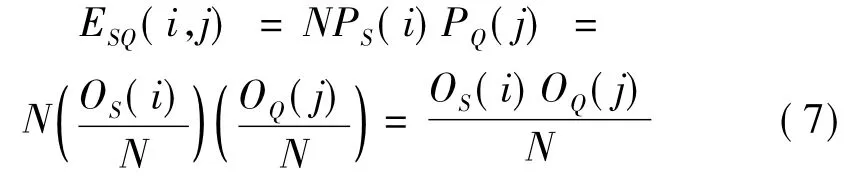
采用等邊緣概率劃分區間，且S，Q用相同劃分區間數NE，邊緣分布密度PS(i)，PQ(j)變為PS(i)= PQ(j)=1/NE，則式(7)變為

此時若已知ESQ(i，j)，則可得NE，取ESQ(i，j)≥5，則式(8)變為

取NE為滿足以上要求的最大整數。當N為NE的倍數時，將S，Q軸分別按等邊緣分布概率劃分為NE個區間，則式(2)可變為

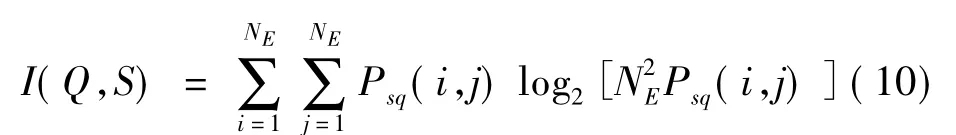
當N不是NE的倍數時則按要求確定NE，即按NE劃分SQ平面后，所有區域內實際點數滿足OSQ(i，j)≥1;80%區域內滿足OSQ(i，j)≥5。判別是否滿足第二要求所用均勻分布卡方檢驗完成，卡方檢驗公式為

卡方檢驗中所用自由度ν=(NE－1)2，則數據對在SQ平面內均勻分布概率為

1.3 Cellucci算法缺陷

該算法缺陷為:當時間序列S或Q長度不能整除劃分區間數NE時其計算的互信息出現錯誤。以Lorenz系統中x變量序列為例，Lorenz系統的微分方程為

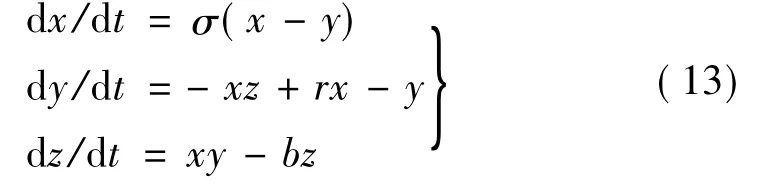
式中:σ=10，b=8/3，r=28。

用4階龍格－庫塔獲得100 000點離散序列，起始點為(8.331，13.291，18.063)，時間步長0.01，其中前4 096個數據點三維圖見圖4，該過程用Tisean3.0.0［8］完成。

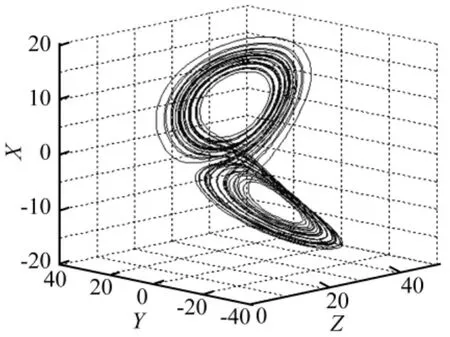
圖4 Lorenz吸引子三維圖Fig.4 Three－dimension diagram of 4096 Lorenz data pairs whose original

S，Q長度取4 096，按等邊緣分布對其劃分2等份，劃分后SQ平面各區域內數據點數用矩陣表示。延時點數1、10、100、200的兩時間序列等份后各矩陣為

按等邊緣分布對S，Q分別劃分4等份，延時點數1、10、100、200的兩時間序列等份后各矩陣為

由各矩陣看出，對SQ平面按等邊緣分布2等份時數據對點分布矩陣中無零元素，需進一步劃分確認是否存在子結構或零元素;對SQ平面按等邊緣分布4等份時矩陣中出現零元素，對SQ平面進一步細分時對應的新矩陣中元素亦為零，與算法［7］中要求所有區域內數據對數大于1不符。即數據對數非劃分區間整數倍時，用該算法對SQ平面等邊緣概率劃分將會僅二等份，致最佳延時不準確。4 096(非NE倍數)與4 500 (NE倍數)個數據點按算法［7］計算的Lorenz與Rossler延遲點數1～200的互信息見圖5。

圖5 不同長度數據序列Cellucci法所求互信息Fig.5 Mutual information fromCellucci's algorithm with different series lengths

此外，其它長度的Lorenz、Rossler序列亦存在相同情況，且Cellucci算法中用于確定等邊緣分布劃分區間數的另個判據較復雜，程序不易實現。

2 互信息改進算法

2.1 最末邊緣區間分布點數處理

在Cellucci算法基礎上本文提出改進算法。以滿足式(9)最大整數NE為等邊緣分布劃分S或Q軸區間數，每個區間內數據點數取小于或等于N/NE的最大整數N1，以N1由小到大依次劃分S或Q軸直至結束。若N/NE為整數，則劃分后各邊緣區間內數據點數完全相同;若N/NE不為整數，則劃分后S，Q軸最末個邊緣區間內分布點數少于其它區間。此時按最后一個區間分布點數與前各區間分布點數的比例進行修正，即設N2為N整除NE時所得余數在最后一個邊緣區間內各區域分布點數得出后分別乘以N1/N2，得各區域內新的分布點數，在計算互信息時最后一個區間點總數則按N1計算，此時的概率分布矩陣用C表示。

2.2 概率分布矩陣計算

由式(2)知，互信息值大小取決于劃分SQ平面后各區間的概率分布矩陣。在等邊緣概率劃分區間前提下分布概率矩陣只與各元素在其序列中大小順序有關，與序列中各元素具體數值大小無關，因此在不改變各數值大小順序前提下對兩序列中數值進行任意變換，可簡化SQ平面內各區域的分布概率判斷。判斷各區域內分布點數時所用方法為:①對S，Q兩序列分別排序，并用S，Q各元素在其序列中的大小順序值代替實際值，分別用兩向量A、B表示，無論S、Q數值范圍大小，A、B所含數據均為1～N的整數，判斷各區域內分布點數則可直接用A、B完成;②因已知每個邊緣分布區間所含點數為N1，則可依次判斷數據對(A(i)，B(i))(i=1，2…N)所在區域，并將區域概率分布矩陣C中元素C(m，n)加1，其中m為1+A(i)/N1最大整數，n為1+B(i)/N1最大整數。

獲得概率分布矩陣C后用第一種處理方法時式(2)變為

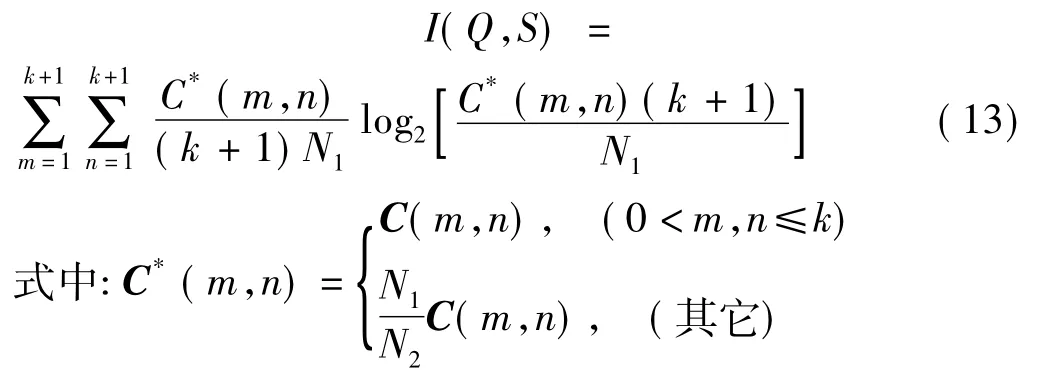
3 改進算法驗證

為確認算法的有效性需對最佳延遲時間進行驗證，用相空間重構的非線性不變量，即利用Lyapunov指數、關聯維數等判斷重構效果［9－10］。本文用最大Lyapunov指數作為判斷依據。該指數計算有兩條途徑，即①已知系統微分方程或映射關系，利用該指數的定義或系統微分方程的雅可比矩陣特征值在一段時間內的平均值計算獲得Lyapunov指數譜［11］，其中最大值即為最大Lyapunov指數;②已知系統試驗的時間序列，則重構后數據可由小數據量［12］、Wolf［13］、BBA［14］等方法及改進算法獲得Lyapunov指數，其中小數據量法與Wolf法所得為最大Lyapunov指數，BBA法可獲得所有Lyapunov指數譜。

對Lorenz系統，由于微分方程已知，由①可得理論的最大Lyapunov指數。Lorenz系統雅可比矩陣為

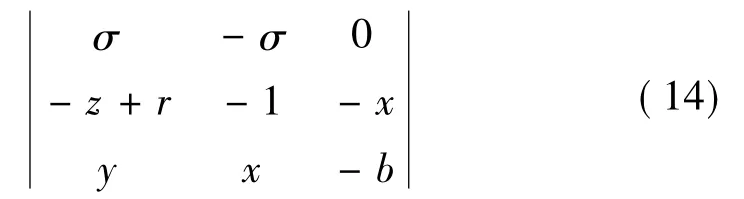
通過4階龍格－庫塔法獲得該系統中不同變量的時間序列，由時間序列可由②獲得另個Lyapunov指數，所得指數值與理論指數值接近程度則可反映重構效果的好壞，即所選延遲時間與嵌入維數的好壞。

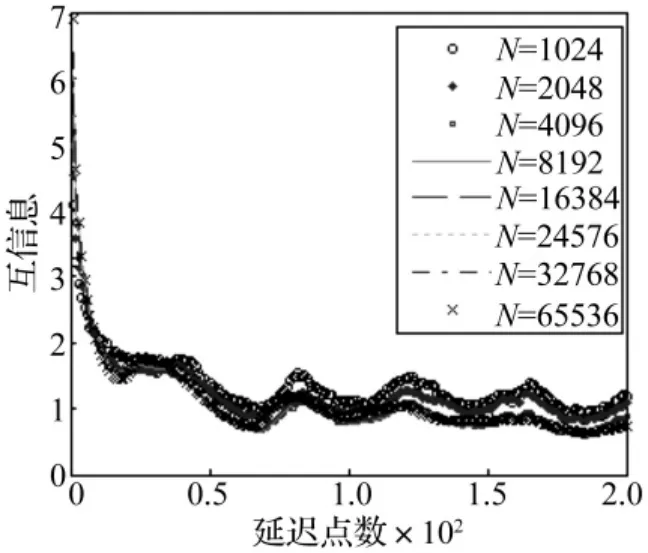
圖6 不同數據長度的互信息Fig.6 Mutual information by different pointslengthes

分別用Lorenz系統中變量x的前1 024、2 048、4 096、8 192、16 384、24 576、32 768、65 536個數據點進行互信息計算。據改進算法所得1～200延遲點數時互信息見圖6。計算過程中各數據點數對應參數見表1。由表1看出，用于計算互信息的序列長度較短時計算結果與穩定值有一定偏差，而隨采用數據長度增加，用以上方法所得第一最小互信息點即最佳延遲時間均趨于穩定;用于計算互信息的序列長度大于等于16 384后最佳延遲點數均為17。

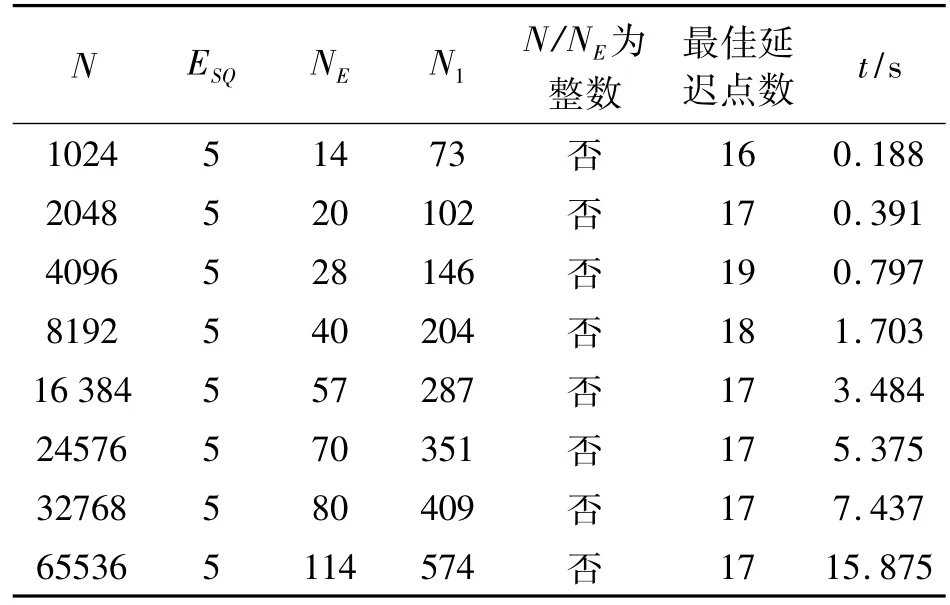
表1 不同數據長度計算互信息時參數Tab.1 Parameters appearing in the process of mutual information calculation by series with different lengths

以上計算互信息算法均在Matlab6.5上實現，所用計算機CPU頻率3 GHz，內存2 GB。由數據長度計算時間知，改進方法的計算時間遠小于Fraser算法，相同運行環境下用Fraser算法計算長4 096序列互信息費時已超200 s。

表2 兩種方法所得最大Lyapunov指數Tab.2 Maximal Lyapunov exponents gained from Jacobi matrix and phase space constructed by time series with different time delay

據Takens定理，采用大于2倍于分形維數的嵌入維數構造相空間時重構的相空間與原系統非線性不變量［15］相同。已知Lorenz序列的分形維數為2.07［16］，故本文嵌入維數取5，通過產生的100 000點時間序列對相空間進行重構，由重構數據通過小數據量法計算出最大Lyapunov指數，該計算過程可直接用Tisean 3.0.0完成。用Lorenz系統方程的雅可比矩陣通過QR分解方法獲得理論最大Lyapunov指數。兩種方法計算值見表2。由表2看出，延遲時間取17時小數據量法所得最大Lyapunov指數與理論值相差0.276%，與最佳延遲時間18相差僅1點。

4 結論

(1)時間序列長度為等邊緣劃分區間數的整數倍時Cellucci互信息算法有效;反之，時間序列長度不為劃分區間的整數倍時Cellucci互信息算法會獲得錯誤的最佳延遲時間。

(2)對兩時間序列進行排序，可用序列中各數值在序列中大小順序值代替原數值實現時間序列的數值轉換;判斷序列各數值所在等邊緣概率區間方法可得概率分布矩陣，計算速度快，程序易編譯。

(3)數據序列長度較大時用改進的最佳延遲時間計算方法結果更穩定;改進互信息算法計算時間遠小于Fraser互信息算法。

(4)用改進互信息算法的最佳延遲時間所得Lyapunov指數與理論值的相對誤差較小，表明該算法有效可靠，可消除Cellucci互信息算法缺陷。

(5)本文互信息算法構造中均設每個區域內平均分布5個數據點，雖所得最佳延遲時間近似值較準確，但該假設是否合理尚需理論推導;是否有其它值作為每個區域內平均分布點數獲得更準確結果有待驗證。

［1］He Qing－bo，Du Ru－xu，Kong Fan－rang.Phase space feature based on independent component analysis for machine health diagnosis［J］.Journal of Vibration and Acoustics ASME，2012(2):10－14.

［2］Zhang Hong－wei，Li You－rong，Xiao Han，et al.Bearing fault diagnosis based on weighted phase space reconstruction［C］. Digital Manufacturing and Automation，IEEE International Conference，2010:315－318.

［3］Fraser A M，Swinney H L.Independent coordinates for strange attractors from mutual information［J］.Physical Review A，1986，33(2):1134－1140.

［4］Mosteller F，Tukey J W.Data analysis and regression［M］. Addison－Wesley，1977.

［5］Bendat J B，Piersol A G.Measurement and analysis of random Data［M］.New York:John Wiley，1966.

［6］Rissanen Y.Stochastic complexity in statistical inquiry［C］. World Scientific，Singapore，1992.

［7］Cellucci C J，Albano A M，Rapp P E.Statistical validation of mutual Information calculations:comparisons of alternative numerical algorithms［J］.Physical Review E，2005(71):1－14.

［8］Hegger R，Kantz H，Schreiber T.Practical implementation of onlinear time series methods［C］.The Tisean package，CHAOS，1999:413－435.

［9］Kantz H，Schreiber T.Nonlinear time series analysis［M］. Cambridge:Ambridge University Press，2004.

［10］Edward O.Chaos in dynamic system［M］.Cambridge: Cambridge University Press，2002.

［11］Kawabe T.Indicator of chaos based on the riemannian geometric approach［J］.Physical Review E，2005(71):1－4.

［12］Rosenstein M T，Collins J J，De Luca C J.A practical method for calculating largest Lyapunov exponents from small data sets［J］.Physical Review D，1993(65):117.

［13］Wolf A，Swift J B，Swinney H L，et al.Determining Lyapunov exponents from a time series［J］.Physical Review D，1985(16):285－317.

［14］Brown R，Bryant P，Abarbanel H D I.Computing the Lyapunov spectrum of a dynamical system from observed time series［J］.Physical Review A，1991(43):2787－2906.

［15］Takens F.Detecting strange attractor in turbulence［J］. Lecture Notes in Mathematics，1981(898):361－381.

［16］Viswanath D.The fractal property of the Lorenz attractor［J］.Physical Review D:Nonlinear Phenomena，2004(190): 115－128.

Improved mutual information algorithm for phase space reconstruction

JIANG Ai－hua1，2，ZHOU Pu1，ZHANG Yi1，HUA Hong－xing2
(1.704 rsearch Institution，China Shipbuilding Industry Corporation，Shanghai 200031，China;
2.State Key Laboratory of Mechanical System and Vibration，Shang Hai JiaoTong University，Shanghai 200240，China)

The mutual information algorithm was improved for gaining rapidly and reliably the time delay in phase space reconstrution of time series.The defect of Cellucci＇s mutual information algorithm was analyzed based on respectively partitioning the plane，constructed by a pair of Lorenz series with the same size，into four or sixteen grids with equal distribution probability in elements on each axis.The improved mutual information algorithms was then promoted based on the original probability matrix that shows the distribution of points corresponding to data pairs of Lorenz series on the plane via the process of sorting the two series，replacing each numerical value by its order number in its own series so as to judge in which data set the element is located and revising the last column and row of the matrix.Finally，after reconstructing the phase space with the optimal time delay，the comparison between the maximal Lyapunov exponent calculated by Rosenstein＇s algorithm from time series and that gained by Jaccobi matrix from Lorenz equation was used to confirm the validity of the new mutual information algorithm.The results show that Cellucci＇s mutual information algorithm may lead to wrong optimal time delay when the series size is not a multiple of elements.The new algorithm，whose result is steadier when large numbers of data pairs are used，can not only eliminate the default of Cellucci＇s algorithm but also is faster than Fraser＇s algorithm.Besides，the lesser difference between the maximal Lyapunov exponents calculated by the two algorithms shows that the new mutual information algorithm is available and feasible.

phase space reconstruction;time delay;mutual information;maximal Lyapunov exponent

023

A

10.13465/j.cnki.jvs.2015.02.014

2013－06－02修改稿收到日期:2013－09－10

蔣愛華男，博士生，1980年11月生

華紅星男，教授，博士生導師，1954年生郵箱:hhx@sjtu.edu.cn