遺傳算法組卷的研究與設計

倪雪飛 孫吉花

【摘要】在線考試系統中的自動組卷技術是系統的核心，是近年來的一門綜合新興學科，它是根據每次的考試要求通過系統來實現自動生成考試試卷，從而克服傳統的一些弊端。本系統考試的要求包括：考試人員類被，考試方向，考試試題類別，試題數量，試卷分值，試題分值，考試時間等參數。通過考試了解當前階段的任務完成情況和存在的不足。自動組卷能夠避免考試中因為人為主觀因素造成的影響，自動組卷技術已經被越來越多的在線考試系統采用。

【關鍵詞】自動組卷 ?遺傳算法 ?在線考試

當今社會工作節奏的加快，為了能夠增強自己在社會中的競爭力，學習充電是必須的，但是繁瑣的異地資格考試很是浪費時間和精力，在線考試系統就應運而生，在線考試系統需要做到能夠真實有效的考察一個人的知識掌握情況，這就需要在組卷上算法上做到盡量智能化。特別是要避免人工組卷帶來的不安全性和不客觀性，所以在線考試系統采用的組卷技術一般都是自動組卷。其中常見的組卷技術有隨機組卷、回溯組卷和遺傳算法組卷等，下面我們詳細講解遺傳算法組卷。

遺傳算法

遺傳算法概述

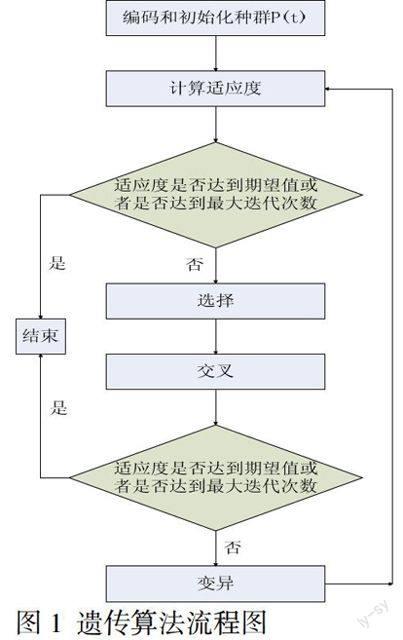
遺傳算法[1]（Genetic？Algorithm，簡稱GA）是一類借鑒生物界的進化規律（適者生存，優勝劣汰遺傳機制）演化而來的隨機化搜索方法，由美國的J.Holland教授1975年首先提出。遺傳算法是一種模擬達爾文的生物進化理論物競天擇的計算模型，通過對自然界生物進化的模擬來解決多約束條件下的最優解。算法實施流程圖如圖1所示

遺傳算法是對種群中的個體進行操作，問題空間的參數通過基因鏈的形式表示出來，編碼的好壞對算法解決問題的能力有直接影響。目前，存在的編碼方式包括二進制編碼、動態編碼、格雷碼編碼[2]、十進制編碼和實數編碼等多種方式。在本系統的組卷應用中，在組卷過程中對數據庫的存取訪問速度受到試題數據結構的影響較大，為了能夠在組卷過程中減少數據訪問的時間開銷，直接以題號作為基因的值，每種題型的題號放在一起，這樣就能快速的獲得指定類型的試題。因此，本系統采用分段的實數編碼方案，比如要組一份“后勤理論”的試卷6道單選，5道多選，3道判斷，2道論述，其染色體的編碼為：

（10，12，3，5，9，40） ?（25，32，21，6） ?（16，51，11） ?（7，26）

單選題 ? ? ? 多選題 ? ? 判斷題 ? ?論述題

在遺傳算法的開始，一般采取的是隨機生成初代種群，以達到遍歷所有狀態的目的。但是這樣會一定程度上延長進化的時間，本文針對系統的使用對象和問題的實際情況，采用不完全的隨機初始化種群的方法，初始化種群的時候就設定試卷的考試方向、各個題型的數量、分數以及考試時間，這樣生成的種群就已經滿足了試卷的一大部分要求，加快了算法的收斂和減少了迭代次數，同時取消了個體解碼時間，提高了求解速度。

適應度函數設計

適應度函數是遺傳算法尋求最優解的依據，一般來說是由目標函數直接轉化而來，通過它來對群體中的個體的優劣程度進行評估，指導算法的搜索方向，因此適應度函數的好還是至關重要的，因此，一份試卷的適應度[3]越高，那么它就越接近算法的最優解，本文在初始化種群中就已經約束了試題方向、分數、考試時間等輔助信息，只需要考慮試卷的難度系數就行了，所以本文中所用的適應度函數是由試卷的難度系數公示轉換而成的。試卷的難度系數為公式1：

（1）

其中Di 為第i道題的難度系數，Si為第i道題的分數 ，n為試卷中試題的總數目。用戶的期望難度EP與試卷的難度P之間的差越小越好。如果一份試卷中期望含有N個知識點，而一個個體試卷中含有M個知識點，那么該份試卷中知識點覆蓋率為 ，上面說到EP和P之間的差值越小越好，知識點覆蓋率則越大越好，本文中遺傳算法的適應度函數為公式2：

（2）

公式2中f1為知識點分布權重，f2為難度系數所占權重，其中f1為零時，那么只考慮難度系數;f2為零時，只考慮知識點覆蓋率，由于本系統使用對象的特點，只考慮難度系數。

遺傳算子

1.選擇算子

選擇算子[4]的主要作用是根據個體的適應度大小決定個體是被選中還是淘汰，這樣適應度高的個體生存機會就要高一些，為了讓遺傳算法在組卷中發揮更好，本文采用的是輪盤賭方法，根據個體的適應度的不同，個體被選中的概率為公式5-1所示，通過公式可以看出，個體的適應度越高，被選中的概率就越大，這樣優秀的個體就能夠得到保留。

2.交叉算子

本文在對個體進行染色題編碼的時候采用的是分段實數編

碼，所以交叉就采用了分段單點交叉策略，具體實現過程為：隨機選擇個體使其兩個為一組，通過交叉概率Pc和適當的條件進行交換，產生兩個新的個體，其中Pc的選擇會影響到算法的收斂性，如果Pc過大，產生新個體的速度就越快，但是容易使得優秀個體遭到破壞，而Pc過小，則會使的搜索過程緩慢。

3.變異算子

在對個體進行交叉后，對個體的基因進行基于概率Pm進行基因變異，這個概率一般較小，對Pm的設置不能過小，如果過小不易產生新個體，如果過大就變成了純粹的隨機搜索。本文在交叉的時候采用了分段單點交叉，這里就不進行分段變異了，而是對整個基因的某段上的某個基因進行變異。通過隨機生成一個[1，n]的隨機數r，r作為一個變異位置，然后從題庫中選取一個變異基因，在選取的時候要保證新選擇的基因要與原基因具有相同的題型，相同的分數，相同的考試方向。

遺傳算法控制參數設置[5]

遺傳算法的多個參數中交叉概率Pc和變異概率Pm對算法的影響較大，其中Pc的選擇會影響到算法的收斂性，如果Pc過大，產生新個體的速度就越快，但是容易使得優秀個體遭到破壞，而Pc過小，則會使的搜索過程緩慢。而Pm的取值的大小同樣影響算法的性能，在保持群體保持多樣性的前提下Pm不能設置過大，如果Pm取值過大，會使算法變為隨機搜索，Pm取值過小，個體的多樣性就無法得到滿足，從而使得算法陷入局部最優的狀態，而過早收斂。為了避免因為交叉概率和變異概率取值造成算法性能受到影響，加快遺傳算法收斂和有效的避免其陷入局部最優狀態，同時保持較為優良的試卷個體，本文采取交叉概率 Pc 和變異概率 Pm 的自適應策略，即使得交叉概率 Pc 和變異概率 Pm能夠隨適應度自動改變，當種群的個體趨于一致或者陷于局部最優時，交叉概率Pc和變異概率 Pm就增加，當群體適應度比較分撒時，交叉概率 Pc 和變異概率 Pm就減小。

可以通過實驗對Pc和Pm的值進行設定從而取最佳值，通過實驗可以Pc取值范圍在0.2～1.0之間時，組卷的成功次數多，而迭代次數少，在組卷方面呈現先增后減，在迭代次數上呈現先減后增。Pm取值過大時，組卷的成功率較低，迭代次數增加，這是由于變異造成的群體中優良的個體遭到了破壞，但是取值過小產生新個體的速率就會降低，導致種群不能實現多樣性。當種群規模較小時，組卷成功率很低，因為種群的規模本身就小，這樣就不具備多樣性的特點，使得算法的搜索空間局限性很強，出現了未成熟收斂的情況。隨著種群規模的提高，算法的搜索空間加大，這樣組卷的成功率也提高，但是平均迭代次數也會隨著種群的提高而提高，這樣也會影響算法的效率。

【參考文獻】

[1]陳國良、王熙發等，遺傳算法及其應用，北京：人民郵電出版社，2001，1～400

[2]李華山;格雷碼的代數結構和分形生成的遞歸算法[J];北方工業大學學報;1996年01期

[3]Holland J. Adaptation in Natural and Artifical Systems[M].AnnArbor：The University of Michigan Press，1975，1～50

[4]王小平，曹立明.遺傳算法一理論、應用與軟件實現[M].西安：西安交通大學出版社，2002

[5]劉學增，周敏. 改進的自適應遺傳算法及其工程應用[J]. 同濟大學學報（自然科學版）. 2009（03）