中學數學新手
潘振華
【摘要】新手與專家教師都用邊講邊問的形式取代單純的講授,提問密度較高.兩類教師都重視雙基的落實,設置了大量的識記型和理解型問題.專家教師善于設計導向型和策略型問題,組成“問題鏈”,啟發學生思維活動,保證學生思維趨向教學目標,幫助學生提煉數學思想方法,引導學生領會數學的本質.兩位教師都比較保守,沒有提出開放型問題,這對培養學生思維的發散性、創造性都是不利的.
【關鍵詞】課堂提問類型;中學數學;新手教師;專家教師;比較研究
一、研究背景
90年代以來,新手—專家教師的比較研究成為教師成長研究的重要課題.課堂提問是整個課堂的“經脈系統”,是成功課堂的重要因素.研究課堂提問是否有效對促進新手教師快速成長有著極其重要的意義.
課堂提問是教師在課堂教學過程中,根據教學目標、教學內容和學情等設計問題并進行教學問答的一種教學形式.課程改革后,課堂提問受到了越來越多的關注,但總體研究的水平仍然偏低.當前課堂提問研究的主體是一線教師,多提問技巧的經驗總結,研究類型以思辨的“理論探討”為主.近年來,對數學新手教師和專家教師的比較研究主要集中在知識結構、教師本身的能力方面,對其進行的實證研究也主要集中在課堂整體教學情況,針對課堂提問的定性和定量相結合的實證研究甚少.
二、研究目的
本研究通過開發中學數學課堂提問類型觀察表,對新手與專家教師開設的兩節“同課異構”的數學課進行比較,并對課堂提問進行了分類、分析,總結專家教師課堂提問的有效類型,科學指導新手教師盡快掌握課堂提問技能,縮短新手教師的成長周期.
三、研究方法
本人主要采取了文獻法、課堂觀察法、錄像分析法、課堂實錄法、個案研究法、定性與定量相結合的研究法等方法展開研究.
四、研究過程
1.研究對象的選擇
本研究綜合考慮教齡、職稱和榮譽等三方面的情況對新手和專家教師作如下界定:
新手教師(簡稱新手):將職稱為二級或二級以下,教齡在三年以下的教師.
專家教師(簡稱專家):將職稱為高級,教齡在十年以上,同時獲得特級教師或市級以上學科帶頭人、專家型教師稱號的教師稱為專家教師.
根據以上界定,我們選取廈門市某重點中學的一位入職不到一年的見習期教師和一位特級教師作為研究對象.通過對這兩位教師講授的同一節“直線與圓的位置關系”來分析、比較他們在課堂教學中提問類型的特點和差異.為尊重提供案例的教師和研究的需要,隱去教師的真實姓名.
2.研究數據收集
我們利用學校專用錄播教室,從教師、學生兩個角度對整堂課進行拍攝.為了盡可能多地捕捉教師提問時的肢體語言變化和學生的表情,筆者將拍攝的內容反復觀看,進行多次整理.
3.教師提問類型
我國學者在參考了Bloom認知領域分類的六個層次,即知識、理解、應用、分析、綜合和評價,提出諸多課堂提問的分類.如顧泠沅將問題類型分為常規管理性、記憶性、推理性、創造性及批判性問題等五種類型.葉立軍在其博士論文中,參考了Bloom的分類,又結合教學中提問的作用和目的,將提問分為管理、識記、重復、提示、理解、評價等六類.筆者參照以上研究,結合自己在教學研究中積累的經驗,將提問類型分成以下六類:識記型、判斷型、理解型、導向型、策略型和開放型.
(1)識記型:目的在于讓學生回憶并記住某一知識點.要求學生就基礎知識(如概念、公式、定理、法則等)或基本程序等進行復述.
(2)判斷型:目的在于讓學生對基本的事實進行簡單的判斷.學生基本不需思考就可回答.
(3)理解型:目的在于讓學生進行推理論證或歸納總結.要求學生運用推理對要解決的問題作出說明或論證,也可對已學的內容進行總結.
(4)導向型:目的在于啟動學生思維,指向問題解決的目標.所提問題具有導向性,也是一種啟發性提問.教師回答,也可以學生回答或不回答.
(5)策略型:即目的在于幫助學生掌握解決問題的策略.主要是以知識為載體引導學生總結解題思路,提煉數學思想方法.
(6)開放型:即目的在于引導學生多方向思維,多角度、深層次地思考問題、問題結果是不可預料的.
五、統計結果及分析
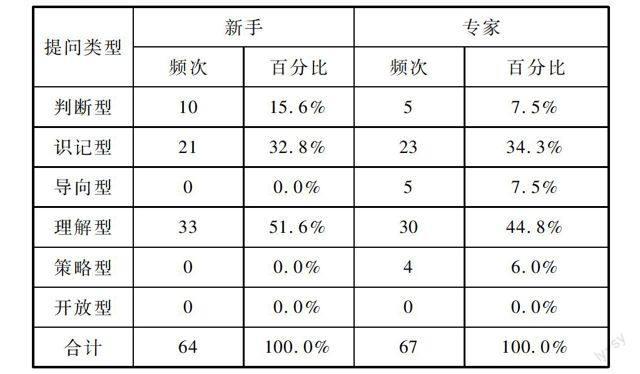
通過對新手與專家在“直線與圓的位置關系”一課中課堂提問進行觀察、記錄、分類、整理,得出以下課堂提問觀察統計表:
(說明:頻次是在課堂提問中出現某一類型的次數,百分比是某一類型出現的頻次與總次數的百分比.)
從上表可以看出,在這節課中新手與專家提問的總次數分別為64次、67次,用時分別為43分鐘、46分鐘,平均每分鐘提問約1.5次.這樣高密度的提問已成為課堂教學重要形式,教師用邊講邊問的形式取代單純的講授.
具體分析如下:
(1)判斷型問題分別占15.6%和7.5%(這兩個比例分別指新手和專家,以下同).新手提出的判斷性問題是專家教師的2倍.如,新手提出“要想弦AB最長,半徑定沒定?”專家提出:“判斷直線和圓的位置關系,我們用初中的方法行不行?”這樣一些簡單的判斷性的問題,思維含量低.教師提問后,全班學生馬上齊答.在課堂教學中,盡量減少此類問題.
(2)識記型問題分別占32.8%和34.3%,兩類教師相差1.5%,幾乎沒有差異.這節課是初高中知識銜接很緊密的一節課,既用到初中所學的直線和圓的位置關系以及一元二次方程根的判別式等方面的知識,又用到高一所學的點到直線的距離公式.兩位教師都考慮到高一的學生可能對初中的知識出現淡忘,又考慮到文科生思維的特點,設置較多的識記型方面的問題,幫助學生復習基礎知識,這有助于為學習新知做鋪墊,起到“溫故而知新”的作用.
(3)導向型問題所占比例分別為0%和7.5%,有顯著差異.專家通常在問題之間相互銜接的時候,提出導向型問題,使問題組成“問題鏈”,對學生的思維起著導向性的作用.
【案例一】(專家教師)
【師問】剛才我們研究的是什么呢?
【師答】是直線的方程確定了,圓的方程也是確定的.我們用兩種方法都可以解決直線和圓的位置關系.
【師問】如果這個直線是變化的,是怎么變化的呢?
(板書:變式提升練習1,ppt演示題目:已知直線l:x+y-b=0和圓心為C的圓x2+y2-2y-4=0,直線l與圓C相交,則b的取值范圍是.)
【生答】這是平行的直線系.
……
【師問】變式提升練習1是關于平行的直線系.如果不是平行的直線系,又該怎么去解決?
【師】我們來看變式提升練習2.(ppt演示題目:已知直線l:bx+y-2b=0和圓心為C的圓x2+y2-2y-4=0,判斷直線l與圓C的位置關系?)
從案例一可以看出專家善于利用導向型問題引導學生積極思考.專家在提出“剛才我們研究的是什么呢?”這一問題后,又提出了 “如果這個直線是變化的,是怎么變化的呢?”和“那么如果不是平行的直線系,又該怎么去解決?”這兩個導向型問題,這三個問題形成一個“問題鏈”.這樣的設計很精彩,是在學生研究了直線和圓的方程都確定的情況討論直線和圓的位置關系之后,仍然保持圓的方程不變,將直線先變為平行的直線系,再變為過定點的直線系,這樣的問題設計層層遞進,非常符合文科生的認知特點,一步一步引導學生由淺入深地思考問題,起到啟發學生思維的作用.
(4)理解型問題所占比例分別為44.4%和36.7%,沒有顯著差異,均占總問題的三分之一以上.說明兩位教師都非常重視培養學生的推理能力和歸納概括能力.
(5)策略型問題所占比例分別為0%和6.0%,有較顯著差異.說明專家重視數學思想方法教學,有利于學生掌握數學學習方法,提升數學思維能力.
【案例二】(專家教師)
【師問】原來我們只是判斷直線和圓的位置關系,我們用初中的方法行不行?
【生齊答】行.
【師講述】那就是圓心到直線的距離與半徑的關系確定了,位置也就確定了.
【師問】但是如果要求交點的坐標就要用高中的這種方法.什么思想?
【生答】方程的思想.
【師講述】也就是說把直線與圓相交與否,轉化成直線和圓對應的方程組成的方程組有沒有解,將幾何問題轉化為代數問題,這也運用了數形結合的思想.
從案例二中可以看出專家引導學生先總結如果只要解決直線和圓的位置關系的問題用初中的方法就行了,但是要求交點的坐標就要用到高中的方法,提出運用“什么思想?”這一策略型問題,在學生得出“方程的思想”后,專家進一步引申為 “將幾何問題轉化為代數問題,這也運用了數形結合的思想”.這種策略型的問題,能幫助學生將所學知識融會貫通,解一道題會一類題,起到舉一反三的作用.
(6)開放型問題均為0個.說明兩位教師在教學中都比較保守,課堂上不會出現學生思路過于發散的情況.
六、研究結論
綜合以上定量研究得出的結果和課堂觀察中的總體印象,得出以下結論:
(1)新手和專家都設置了大量的識記型和理解型問題,這兩類問題分別占84.4%和79.1%.說明這兩類教師都非常重視基礎知識、基本技能的理解和掌握.
(2)專家善于設計導向型和策略型問題,共有9個,占15.5%.專家常常在從一個問題向另一個問題過渡時提出導向型問題,使問題組成“問題鏈”.這類問題幫助學生弄清前后問題的聯系和區別,不僅啟發學生思維活動,還能保證學生思維趨向教學目標.專家通常還會在解決一個問題之后會提出策略型問題,幫助學生提煉數學思想方法,領悟數學的本質.
(3)兩位教師設計的問題都是封閉型問題,沒有開放型問題.說明兩位教師都不敢放開,這對于應付高考這樣的幾乎都有唯一標準答案的考試有益,但對啟發學生的創新思維是不利的.
七、進一步思考的問題
任何一個優秀教師,專業成長都要從新手開始,經過熟手階段,最后成為專家教師.本研究選取的素材只是一個個案的分析,一些結論也只是一家之言,帶有一定的主觀性.目前正在通過擴大研究數量,開展多節課的新手與專家教師在課堂提問上的對比研究,試圖探尋兩類教師在課堂提問上的一般特點和差異,幫助新手教師提升課堂提問技能.
【參考文獻】
[1]顧泠沅,周衛.課堂教學的觀察與研究——學會觀察[J].上海教育,1999 (5):14-18.
[2]葉立軍.數學教師課堂教學行為比較研究[D].[博士學位論文].南京:南京師范大學,2012:59.
[3]宋曉平,王建華.數學課堂學習動力與“教學用問題”研究[J].數學教育學報,2006,15(3):19-23.

