淺談設問在激發初中學生數學課中思維積極性的作用
張永金


在實施素質教育的過程中,如何更有效地提高課堂效率已成為眾多教師探索的問題。而激發與引導學生的思維則是提高課堂效率的關鍵。亞里士多德說過:“思維從對問題的驚訝開始”。為了培養學生的思維能力,古今中外的教育家無不注重問題的設計,那么教師應該如何在教學過程中精心地設計問題以達到有效、持續地促使學生積極思維的目的呢?下面結合本人的數學教學實踐談談自己的一些看法。
二、循循善誘,保持學生堅決思維的持續性
在恰當的問題情境中,學生思維的積極性被充分調動起來,但怎樣讓學生這種思維的積極性保持下去并真正轉化為好的教育效果呢?
1、設問啟發要與學生的主體思維相吻合
教師提出問題后,要留給學生足夠的時間讓學生獨立思考或集體研究討論,必要時教師才給予適當的啟發引導。教師的設問啟發要遵循學生思維的規律,因勢利導,循序漸進,不要強制學生按照教師提出的方法和途徑去思考問題,喧賓奪主。因為最重要的往往不是問題的結論,而是學生運用已有的知識、能力不畏艱難的探求結論的過程,這時學生在智力情感等方面才會有真正的提高和收獲。
例如:初中學生在學習“三角形相似的識別”這一內容時,教師常常會選用如下的例題:
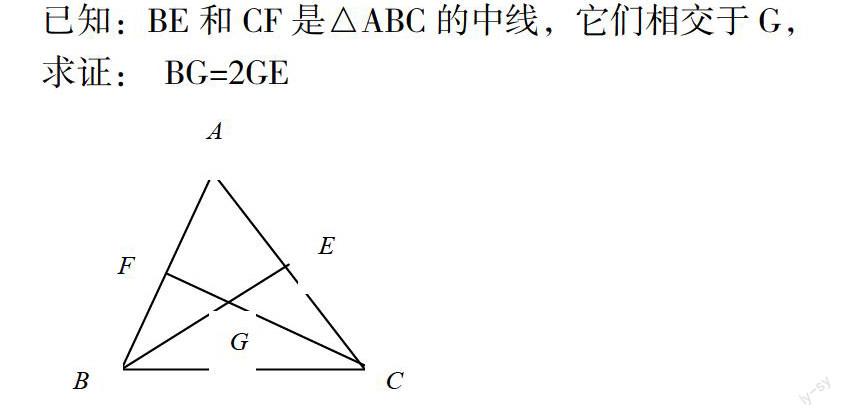
已知:BE和CF是△ABC的中線,它們相交于G,
求證: BG=2GE
有些教師在學生一時沒有解題思路時往往會急于引導學生想到連結輔助性EF,然后證明△EFG∽△BCG。這樣一來教師就可能限制和干擾了學生獨立的思維過程,沒有與學生的思維同步,有經驗的教師在備課時,總是會事先認真揣摩學生的思維心理,估計學生思維可能發生的各種情況,先將不正確的思路排除,再將學生引入正途。對于這道例題,學生可能會去證明△BGF和△CGE相似,教師要讓學生議論,先說明這兩個三角形不一定相似,即使相似,也不符合求證的要求,這就為學生釋去了疑慮,這時不須啟發,學生也會利用E,F分別為AC、AB的中點的條件,想到連結EF。
2、不斷為學生設計富有啟發性的問題
數學思維的過程就是不斷地提出問題和解決問題的過程。因此,在數學課堂學習中,教師要不斷地向學生提出新的數學問題,為學生的數學思維活動不斷提供動力和方向,使數學思維活動持續不斷的向前發展。合適的數學問題必須符合下列條件:
① 問題要有方向性。②問題要有啟發性。③問題的難度要適中。問題并不在多少,而在于是否具有啟發性,是否是關鍵性的問題,是否能夠觸及問題的本質,并引導學生深入思考。如前面“用三角形玻璃被打碎成兩塊來引入三角形全等識別”的例子中,若學生無法自己找到解答方法的話,教師就可以這樣設問來為學生思維搭臺階:“若帶第一塊碎玻璃去,則帶去了原三角形邊角中的幾個元素?若帶第二塊碎玻璃去,則又帶去了原三角形邊角中的幾個元素?”這就是一個極為關鍵性的富有啟發性的問題,它引起了學生的深入思考,并為學生學習 “角邊角公理”奠定了基礎。
總之,在數學課堂教學中,精心巧妙地不斷為學生設計具有啟發性的恰當問題,對于激發與引導學生的積極思維和研究探索數學問題的積極性會起到巨大的作用,特別是對于培養學生的創新精神和實踐精神都有十分深遠的意義。

