“正切函數的圖像和性質”的教學設計
潘承美
“正切函數的圖像和性質”是全日制普通高級中學教科書(必修)《數學》第一冊(下)第四章第十節的內容,也是普通高中課程標準試驗教科書(必修)《數學》4 §1.4.3的內容.
正切函數的圖像和性質的學習是正弦、余弦函數的圖像和性質知識的延續和深化,也是數形結合等重要數學思想方法的基礎.本節課的教學不但能使學生在原有知識和經驗的基礎上進一步體會數形結合思想,而且可以提高觀察、比較、概括等能力的發展.但對圖像的認識學生始終有些難以理解,因此,本節課力爭使用多媒體教學,使學生從理性和感性兩方面去認識,從而達到預期的效果.
一、教學目標
1.知識目標
通過本節的學習能理解并掌握作正切函數圖像的方法,能用正切函數的圖像解決有關問題.
2.能力目標
經歷正切函數圖像的作法過程,發展學生運用類比的方法分析問題和解決問題的能力,并讓學生進一步體會數形結合思想方法的重要性.
3.情感目標
培養學生積極參與、合作交流的主體意識和主動探索、勇于發現的科學精神.在知識的探索和發現的過程中,使學生感到數學學習的意義,從而產生良好的數學學習態度.
4.重點和難點
重點:正切函數的圖像形狀及其主要性質.
難點:利用正切線畫出正切函數y=tanx,x∈-π2,π2的圖像.
為了突出重點、突破難點,在教學中采取以下措施:
(1)采用類比的方法,讓學生在正弦函數圖像畫法的基礎上研究正切函數圖像的畫法.
(2)從學生已有的知識出發,利用數形結合的思想,逐步引導學生通過自主探索、合作交流的形式,觀察、歸納出正切函數的主要性質.
二、教法探索
1.教法分析
針對高一年級學生的年齡特點和心理特征,結合他們的認知水平,在遵循啟發式教學原則的基礎上,本節課我主要采用以“情境——問題”教學法為主,以類比法、討論法、練習法為輔的教學方法,意在通過教師的引導,調動學生的積極性,讓學生多交流、多討論,主動參與到教學活動中來.
“情境——問題”教學法是貴州師范大學數學系的教授和研究生們,從跨文化數學教育研究的結果出發,為改變由教師單向灌輸書本知識、學生被動接受學習的模式,提出了旨在培養創新意識和創新能力的基本教學模式,表示為:
設置數學情境→提出數學問題→解決數學問題→注重數學應用
(引導觀察分析)(猜想探究)(正面求解或反例反駁) (學做學用)
2.學法指導
現代教育理論認為,教師的“教”不僅要讓學生“學會知識”,更主要的是要讓學生“會學知識”,而正確的學法指導是培養學生這種能力的關鍵,因此在本節課的教學中,教會學生能用“類比”的學習方法學習正切函數的圖像和性質,體會數形結合解決問題的好處,使傳授知識與培養能力融為一體,真正實現本節課的教學目標.
3.教學手段
為了更形象、直觀地突出重點、突破難點,增大教學容量,提高教學效率,本節課采用多媒體輔助教學,以加深學生對圖像的認識,尤其使用幾何畫板的功能,讓學生用動態的觀點分析問題和解決問題.
三、教學環節設計
為了達到預期的教學目標,對整個教學過程進行了系統的規劃,主要設計了以下五個教學環節(諸環節的標題與順序見下面的各個小標題):
1.創設情境,導入新課
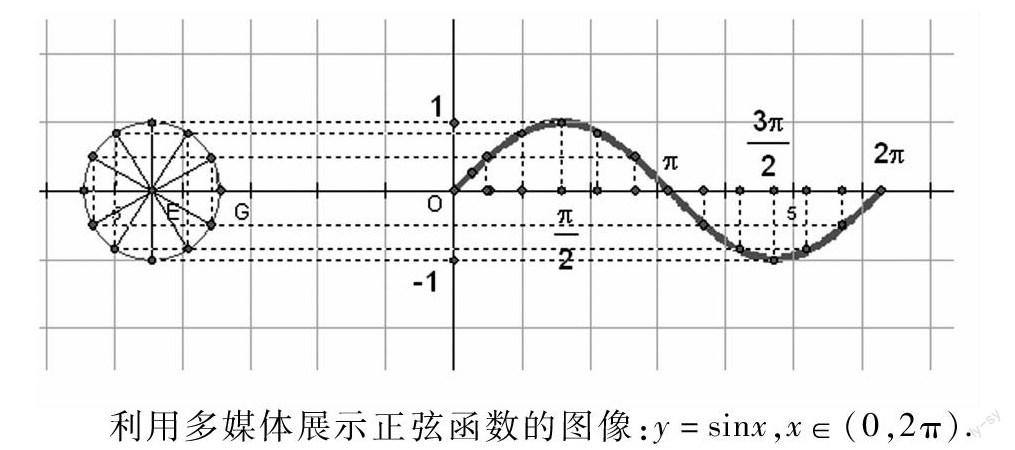
引入新課:正切函數是區別于正弦函數的又一三角函數,它與正弦函數的最大區別是定義域的不連續性,為了更好地研究其性質,我們首先討論y=tanx的圖像.
利用多媒體展示正弦函數的圖像:y=sinx,x∈(0,2π).
2.自主探索,歸納新知
(本環節主要引導學生探索研究,得出新知.引導學生由正弦函數圖像,通過類比作出正切函數圖像,并讓學生通過對圖像的觀察,自主探索、合作交流,歸納出正切函數性質.)
師生互動:
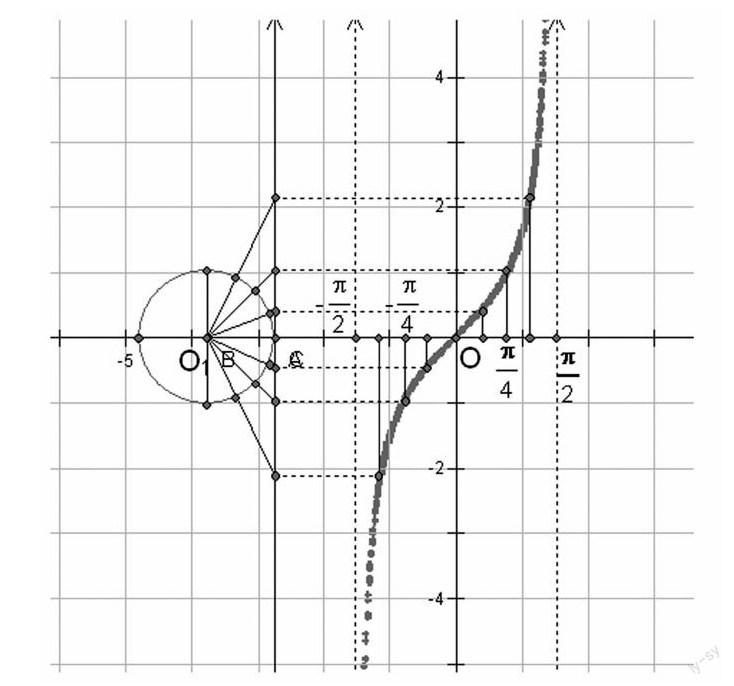
活動一:采用類比的方法,讓學生通過正弦函數圖像的作法探索如何利用正切線作出正切函數的y=tanx,x∈-π2,π2圖像.
在學生合作交流、共同探討后利用多媒體課件展示正切函數的圖像(如圖示).
活動二:利用幾何畫板的強大功能展示正切函數圖像的動態畫法,讓學生在動態中享受數學知識帶來的樂趣.
活動三:引導學生通過函數的周期性作出函數y=tanx在整個定義域內的函數圖像.
(此環節讓學生通過正弦函數的畫法,通過類比的方式,根據正切函數的周期性得出.)
活動四:引導學生通過對圖像的研究,分析歸納出正切函數的性質.
(本環節中,通過設計“問題串”、作類比等方式,使學生對于知識的理解不僅僅停留在表面,而是抓住了其實質,從而輕松地掌握本節的教學重點.)
3.鞏固練習,深化知識
適當的鞏固性、應用性練習是學習新知識、鞏固新知識所必不可少的.為了促進學生對新知識的理解和掌握,及時安排學生完成以下練習.
1.求函數y=tanx+π4的定義域.
2.不求值,比較下列各組中兩個正切函數值的大小:
(1)tan167°與tan173°;
(2)tan-11π4與tan-13π5.
4.歸納小結,反思提高
小結以提問的方式出現.
問題1:通過本節課的學習,你學會了什么知識?
問題2:在解決問題的過程中,你掌握了哪些數學思想方法?
5.布置作業,分層落實
為培養學生良好的學習習慣,鞏固所學內容,提高學生的探究能力和自主學習能力,讓學生完成下列練習:
1.證明函數f(x)=tanx在-π2,π2是增函數.
2.課后習題(習題4.10).
四、反思研究
作為一節新知識課,在教法上,我打破了傳統的教學模式,精心設計問題情境,積極引導、啟發學生,經過類比、觀察、歸納,最終得出.
本節課在設計和教學過程中,留下了一些遺憾.比如,想讓學生了解的內容過多,而對學生的估計不足,使得在教學過程中,未能充分發揮學生的主觀能動作用,教學中未能完全放開.
附:板書設計
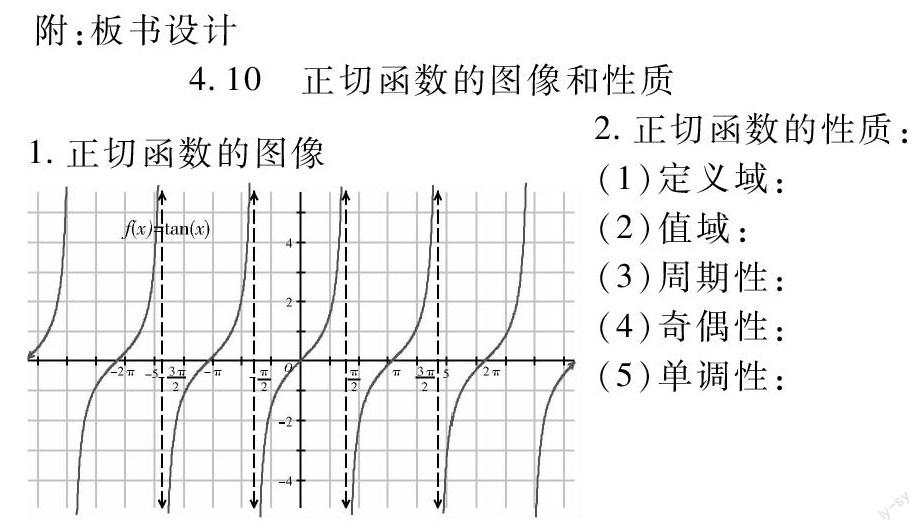
4.10正切函數的圖像和性質
1.正切函數的圖像
2.正切函數的性質:
(1)定義域:
(2)值域:
(3)周期性:
(4)奇偶性:
(5)單調性:
3.練習鞏固.
【參考文獻】
[1]馬復.設計合理的數學教學[M].北京:高等教育出版社,2003.
[2]教育部.普通高中數學課程標準(實驗).北京:人民教育出版社,2003.
[3]呂傳漢,汪秉彝.中小學數學情景與提出問題數學探究[M].貴陽:貴州人民出版社,2002.

