線性回歸在居民家庭收入與支出中的應用研究
陳智勇

[摘要]線性回歸是研究非隨機變量與隨機變量之間關系的重要方法,線性回歸預測是統計學中的重要預測方法。本文以居民家庭收入與支出關系為研究對象,利用線性回歸模型,借助Excel工具,給出二者之間的關系,并且對家庭收入在某個特定值時的支出進行預測,以期給相關工作者提供參考。
[關鍵詞]線性回歸;居民收入;居民支出
[DOI]10.13939/j.cnki.zgsc.2015.13.012
1線性回歸模型簡介
簡單地說,回歸分析是通過建立回歸模型研究相關變量之間的關系并做出相應的估計和預測的統計方法。一元線性回歸是最簡單的回歸分析,其基本步驟是這樣的。
第一步,建立模型。首先應當利用專業知識或者散點圖判斷y與x是否存在呈線性相關關系,其中y是被解釋變量,也是隨機變量;x是解釋變量,也是非隨機變量。若二者之間存在線性相關關系,y與x之間的關系可表達為y=β0+β1x+ε,這里β0是截距,β1是斜率,二者統稱為回歸系數,ε是隨機擾動項。解釋變量x與隨機擾動項ε共同導致了隨機變量y離開均值產生變化。
第二步,估計回歸系數。一般我們采用最小二乘法來計算0和1。我們用直線=0+1x去擬合{xi,yi}(1≤i≤n)這些散點,我們自然要求擬合偏差的平方和Q=ni=1(yi-i)2最小,即Q=ni=1(yi-0+1xi)2最小。Q是0和1的函數,令其對0和1的偏導數為0,可以計算出0和1。引入記號Sxx=ni=1(xi-)2, Sxy=ni=1(xi-)(yi-), Syy=ni=1(yi-)2, 則有公式:
1=SxySxx
0=-1
第三步,回歸方程的顯著性檢驗。
檢驗方程的顯著性,我們只需檢驗β1是否為0。作假設H0∶β1=0。對于給定的顯著性水平α,由于α=P{F>Fα(1,n-2)},若F>Fα(1,n-2),即F只有α的可能性大于Fα(1,n-2),而現在確實大于了,所以我們拒絕H0,認為回歸方程顯著,否則認為回歸方程不顯著。這種方法F稱為檢驗法。
第四步,利用方程進行預測。若回歸方程經過檢驗是顯著的,那么可以將變量取值代入回歸方程求出因變量的預測值。
2線性回歸模型在居民家庭收入與支出中的應用
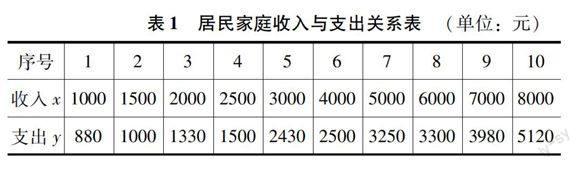
家庭收入與消費的線性回歸:某地區家庭收入與家庭消費支出的調查數據如表1所示。建立家庭收入和家庭消費支出之間的線性回歸模型,并預測家庭收入為9000元時的家庭消費支出。
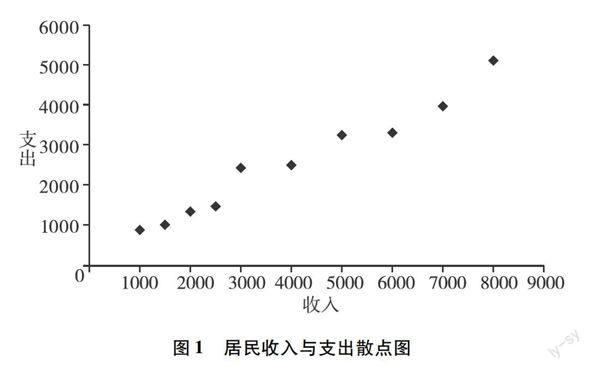
我們觀察散點圖1,可知居民收入與支出呈線性相關關系。
下面,我們按照一元線性回歸的4個步驟來建立回歸方程,預測家庭收入為9000元時的消費支出。
第一步,設支出為y,收入為x,并且二者之間存在線性相關關系,即有y=β0+β1x+ε。其中β0是截距,β1是斜率,統稱回歸系數,ε是隨機擾動項。收入x與隨機擾動項ε共同導致了隨機變量y離開均值產生變化。
第二步,估計回歸系數。我們當然可以第一部分的公式1進行計算,但是其較為煩瑣。我們可以利用統計軟件Excel計算其回歸系數。我們在Excel2010中依次點擊“文件”——“選項”——“加載項”——“分析工具庫”——“轉到”——“分析工具庫”——“確定”可以加載“數據分析工具”。現在,我們可以使用Excel2010的“數據分析工具”進行回歸分析了。由于Excel只能識別縱向數據,所以應當先將數據由“橫向”轉化為“縱向”,使用Excel的“選擇性粘貼”即可實現。
我們點擊Excel2010的“數據”選項卡,再點擊“數據分析”按鈕,這時會出現一個對話框,問你選擇何種分析工具,我們選擇“回歸”。之后,我們根據要求填寫“Y值輸入區域”、“X值輸入區域”(這兩項也可以用折疊按鈕點選),選擇“置信度”為95%,選擇“輸出區域”為新工作表,勾選線性擬合圖,即可得到回歸系數的估計值等一系列的結果。回歸系數的估計值的結果如表2所示。
表2中Coefficients意思是“系數”,Intercept意思是“截距”,Variable意思是“變量”,表2表明x前的系數為259,截距為0.56,回歸方程為:y=0.56x+259;
我們可以畫出收入、支出擬合圖,由圖2可以看出擬合效果非常好。
第三步,回歸方程的顯著性檢驗。上述擬合效果只是直觀感受,方程的顯著性需要進一步的檢驗。我們檢驗方程的顯著性,只需檢驗β1是否為0。現在我們顯著性水平取為0.05,查 分布上側分位數表得Fa(1,8)=5.32。我們用Excel2010的“數據分析工具”得出該線性回歸方程的值為227.47。也就是說,在顯著性水平為0.05下,拒絕假設,回歸方程顯著。
第四步,利用回歸方程進行預測。上面已經證明了回歸方程在顯著性水平為0.05下是顯著的,此時,我們可以利用回歸方程進行預測當家庭收入為9000元時,家庭消費支出的預測值。將11代入線性回歸方程中的x,即可得出11等于5299元。
3結論
本文介紹了一元線性回歸的基本理論,包括概念引入、建立模型、舉例分析和預測等。線性回歸是生產運作中常用的預測方法。為提高使用效率本文使用Excel軟件對一元線性回歸進行分析預測,求解了家庭居民收入與支出之間的相關關系,并且給出了當家庭收入為9000元時的支出預測值,圓滿地完成了本文的任務。
參考文獻:
[1]費宇.應用數理統計——基本概念與方法[M].北京:科學出版社,2007.
[2]陳希孺.概率論與數理統計[M].合肥:中國科學技術大學出版社,2011.
[3]崔鵬,高松,張麗.線性回歸在居民家庭收入與支出中的應用[J].商,2013(23).
[4]齊峰,徐麗麗.關于農民人均收入預測的線性回歸模型[J].科學教研,2013(11).
[5]陳肯界.現金流通與物價指數的實證研究[J].中國市場,2014(44).
[6]賀鏗.中國經濟發展的影響因素與關注點[J].中國市場, 2014(11).
[7]王桃桃.城鎮化對我國城鄉收入差距的影響[J].中國市場, 2014(42).

