中美高中數學教材的習題比較及啟示
——以PEP教材與UCSMP教材中平面向量章節為例

林 丹，胡典順

（華中師范大學 數學與統計學學院，湖北 武漢 430079）

中美高中數學教材的習題比較及啟示
——以PEP教材與UCSMP教材中平面向量章節為例

林 丹，胡典順

（華中師范大學 數學與統計學學院，湖北 武漢 430079）

教材建設是中國新一輪數學課程改革的重要標志，是改革理念和要求的具體體現．通過對人教版高中數學教材與美國UCSMP教材中向量章節習題的比較發現，UCSMP教材的習題呈現方式豐富，編排具有層次性，素材來源與實際生活更緊密，注重較高認知水平的培養，注重習題的探索性和開放性，難度較大；人教版教材習題類型豐富，較高認知水平習題較少，難度恰當，注重基礎性，探索性、開放性問題較少．在教材編寫中，人教版高中數學教材可以適當考慮豐富習題的呈現方式，提高較高認知水平習題比例，增加探索性和開放性習題，注重習題背景的多樣化，緊密聯系生活實際．

數學教材比較；平面向量；習題；啟示

1 問題提出

教材建設是中國新一輪數學課程改革的重要標志，是改革理念和要求的具體體現[1～2]．習題是中學數學教材的重要組成部分，習題配置在一定程度上反映了數學教材編者的價值取向和編寫風格，習題對學生數學概念的理解、數學技能的掌握和數學思想方法的掌握具有不可估量的作用，也對數學課堂教學產生不可忽視的影響．對中美兩國高中數學教材中的習題進行比較，分析兩國教材在習題配置方面不同的風格、傾向及特色，對中國的數學教學改革和高中數學教材習題的編寫是很有必要的．

人民教育出版社出版的教材在中國得到廣泛的使用．在美國，每年有幾百萬中小學生使用The University of Chicago School Mathematics Project教材（以下簡稱“UCSMP教材”），該系列教材是體現美國課程改革及發展方案的典型代表．UCSMP教材強調基本訓練，重視能力培養，著眼于數學應用意識和問題解決[3]．向量是近代數學中重要和基本的數學概念之一，是溝通代數、幾何與三角函數的橋梁．在新一輪數學課程改革的背景下，《普通高中數學課程標準（實驗）》中平面向量知識的份量進一步增加．向量又具有數形結合的重要特征，既有幾何特點又有代數意義，是數學教材中非常重要的數學知識．因此，選取人民教育出版社《普通高中數學課程標準實驗教科書（A版）》（2007版）中必修4[4]（以下簡稱“PEP教材”）和UCSMP教材（2010版）第六冊[5]中平面向量部分作為比較內容，研究中美兩國這部分知識習題的配置情況，為教材平面向量部分的習題編寫提供參考建議．

2 研究方法

PEP教材中平面向量的知識是安排在必修4第二章，UCSMP教材中平面向量的知識安排在第六冊第十二章前4個小節（后面4個小節的內容是空間向量，由于這里主要是比較平面向量的知識，所以不考慮UCSMP教材中空間向量的知識）．采用文本質性分析與定量刻畫相結合的研究方法，從習題的呈現方式、數量、類型、認知水平以及難易程度5個方面進行比較研究．

（1）習題的呈現方式：根據教材中的習題欄目設置進行詳細分析．

（2）習題數量：UCSMP教材和PEP教材中的習題均有兩種形式：含有一個小問題的習題和含有多個小問題的習題．例如UCSMP教材以阿拉伯數字1，2，3……標注習題題號，用小寫字母a，b，c……表示下設的小問題題號；PEP教材也以阿拉伯數字1，2，3……標注習題題號，但是用（1），（2），（3）……表示下設的小問題題號．為統一標準，以阿拉伯數字1，2，3……出現的次數為準來統計習題數目，即以大題計，一題多問的按照一題計算，考慮到習題類型中的題型也需要統計題目，判斷題和選擇題以小題計算．

（3）習題類型：將習題分為：選擇、填空、判斷、解答、證明、作圖等6種常見題型，并對它們分別進行統計．統計方法同習題數統計方法．

（4）習題的認知水平：布盧姆等的《教育目標分類學》在認知領域有6大類別：知識、領會、運用、分析、綜合、評價．他的分類理論由于缺乏可靠的實證，其在連續性和層次性方面存在漏洞．鑒于此，顧泠沅等先后兩次（1990，2007）進行大樣本測試，從大量外顯行為所表征的教學目標中析取內隱主要因素，由此確定目標框架的層次并研究分類的連續性[6]．最后經過改造，數學認知水平分析框架分為4層次架構：水平1：計算——操作性記憶水平；水平2：概念——概念性記憶水平；水平3：領會——說明性理解水平；水平4：分析——探究性理解水平．其中，水平1、2為記憶水平，為較低認知水平．水平3、4為理解水平，屬于較高認知水平，第4水平通常稱作高認知水平．水平1層次的習題只需要學生按照教材所明確要求的程序或方法進行基本的運算；水平2層次的習題是考察學生對課本概念、規則、表達形式記憶的題目；水平3層次的習題需要學生理解概念、定理、法則等的內涵和外延，從而能夠根據課本例題，選擇合適的數學方法，靈活運用所學知識解決一些常規問題；水平4層次的習題需要學生對之前沒有接觸過或沒有現成解決方案的非常規問題（開放題、探究題）進行分析，創造性地解決問題[7]．

（5）習題難度：根據相關學者建立的綜合難度模型[8]，對兩版教材平面向量章節中的習題進行統計分析，其中包含了5個難度因素：探究、背景、運算、推理、知識含量，具體如下表1所示：

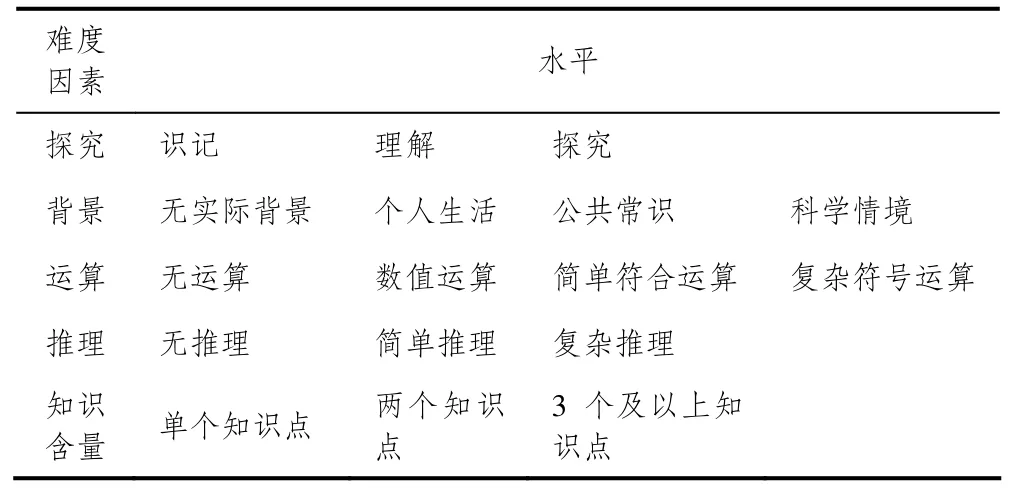
表1 綜合難度因素表

計算習題綜合難度時采用如下計算公式：

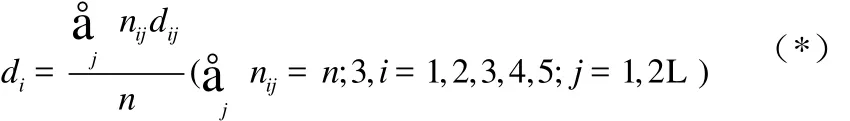
3 研究結果與分析

3.1 習題呈現方式

習題的呈現方式在一定程度上體現了教材編寫的特色，兩版教材的主要習題呈現方式如表2所示．

表2 兩版教材習題呈現方式的比較

分析表2可知，PEP教材習題形式多樣．如“練習”、“習題”、“復習參考題”等．練習題是對所學知識和例題的進一步深化，起到練習的作用；習題一般位于某一大節之后，起到鞏固和綜合的作用，一般是根據相關度較高的知識點模塊分為A組和B組兩類，B組習題難度大于A組習題；復習參考題位于章節最后，題量較大，一般也分為A組和B組，B組習題難度也大于A組，主要是考查學生對整章知識的掌握程度．另外，還有在教材正文中以“觀察”、“思考”、“探究”、“討論”等形式呈現的問題．

UCSMP教材一般是每節后習題、自我測試題和每章末尾的總復習參考題．章節后習題主要分為4個部分：鞏固類題（Covering the reading）、應用類題（Applying the Mathematics）、復習類題（Review）、探索類題（Exploration）．鞏固類題主要是覆蓋教材內容的一些基本題，通過做這類題讓學生掌握教材中所述的一些基本的數學概念、公式及定理；應用類題是把所學到的數學內容應用到具體的實例中去；復習問題主要是一些綜合性題目，讓學生加深對所學內容的理解，不僅包括本章所學內容，通常還包括對之前各章所學知識的鞏固應用；探索類題是一些多解性或開放性的題目，有些還需要學生自己動手收集數據，加以分析并設計解題方案，這顯然是UCSMP教材習題呈現的一大特色．每一章之后，UCSMP教材還有一個自我測試題（Progress Self-Test），題量適中，之后就是一個章末復習題（Chapter Review），題量較大，分為4個部分：技能檢測題（Skills）、性質檢測題（Properties）、應用檢測題（Uses）、表達檢測題（Representations）．每部分的題量都較適中，均涵蓋了本章中的基本內容和重難點知識，從4個部分分層次來考查學生對知識的掌握情況．另外，UCSMP教材每小節習題中的每一題都在題目后用小括號注明所用的知識在哪一章節，章末復習題中每個部分也是分別設置各個小目標，比如技能檢測題中設目標A、B、C、D（Object A、Object B、Object C、Object D），每個目標都注明了涉及的知識在哪個章節．

總的來說，UCSMP教材的習題呈現方式是比較完善的，教材對習題進行細化分層，并進行彈性處理．另外，習題難度呈現階梯狀，體現了不同層次學生的選擇，為學生提供更多的選擇空間．由此可見，UCSMP教材在習題的呈現方式上要比PEP教材更具有多樣性．

3.2 習題數量

兩版教材平面向量的習題數量統計情況如表3所示．在習題數量方面，PEP教材在這一章中設置的總習題數量為140道，平均每節為28道；UCSMP教材為135道，每節為34道，兩版教材習題的數量分布差異不顯著（χ2（1, N=337）=0.461，p>0.1）．兩套教材都設置了較多的習題，均重視習題訓練對學生學習知識和方法的作用．PEP教材在每節后習題訓練的安排上相對較少，一共是63道，占45%，而UCSMP教材在每節后習題數量為84道，所占比例為62.2%，但是PEP教材中“練習”部分的習題要求在課堂當中完成．PEP教材中習題部分A組的題目要遠遠多于B組，強調基礎性原則．UCSMP教材鞏固類題（Covering the reading）所占的題目最多，這部分類似于PEP教材中的習題A組，學生通過課前預習、教師講解之后，大多都可以獨立完成此類題目，題量占其次的是復習類題．最后，PEP教材、UCSMP教材中的章末復習題所占比例分別為26.4%、29.6%，數量相差不多．

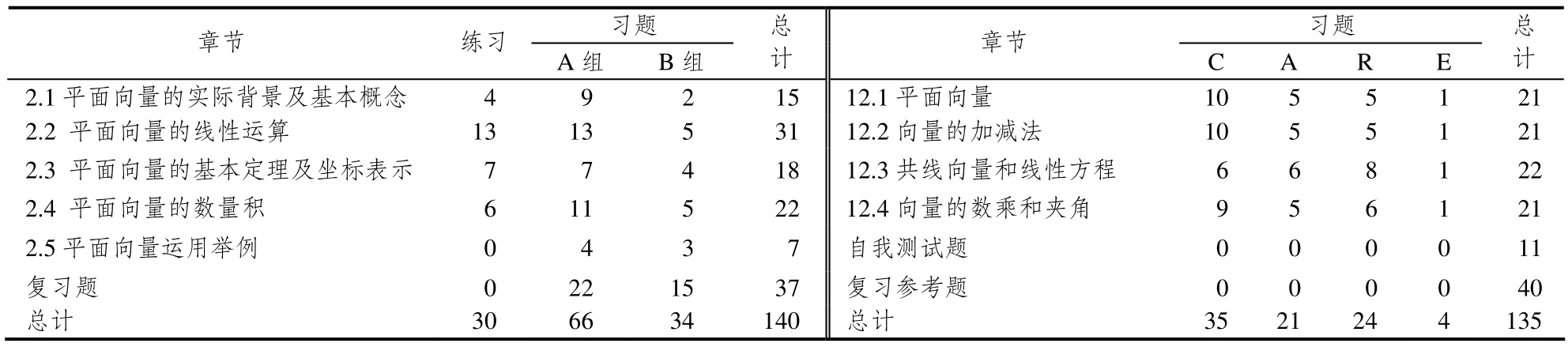
表3 兩版教材“平面向量”習題數量比較

3.3 習題類型

兩個版本平面向量習題類型統計具體情況如圖1所示：

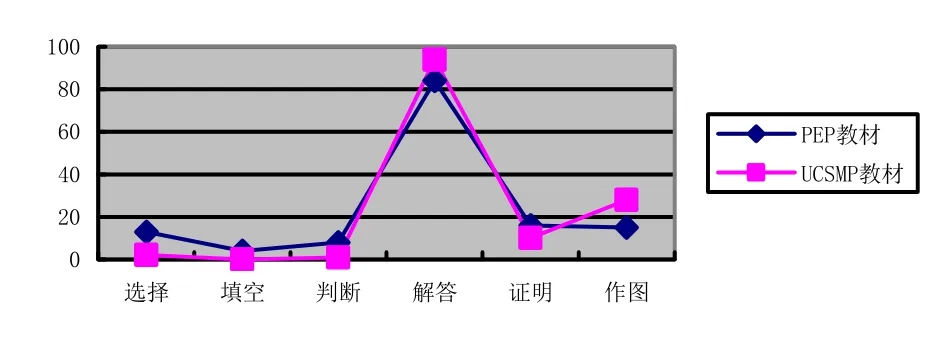
圖1 兩版教材習題類型折線圖

從統計數據來看，在習題的類型上，兩版教材題型都較豐富，兩版教材習題類型分布有顯著差異（χ2（5, N=275）=23.22，p<0.001），其中選擇題、填空題、判斷題等題型兩版教材配置的題量都較少，特別是UCSMP教材的填空題為0道，選擇題只有2道，而且還是多項選擇題，判斷題也只有1道．PEP教材這3者類型的題目數量要更多，選擇題、填空題、判斷題所占比例分別為9.3%、2.9%、5.7%，但PEP教材的選擇題基本只出現在章末復習題，判斷題也是相似的情形．兩個版本的教材中，比例最高的仍然是傳統題型解答題，PEP教材和UCSMP教材解答題各占習題總量的比例分別為60%、69.6%，由此可見，UCSMP教材解答題數量多于PEP教材；其次是作圖題和證明題，PEP教材和UCSMP教材證明題所占比例為11.4%、7.4%，作圖題所占比例為10.7%、20.7%．因此，證明題數量PEP教材比UCSMP教材多，作圖題的比例PEP教材要比UCSMP教材少10%．向量作為連接代數和幾何的工具，其圖形屬性不容忽視．

3.4 習題認知水平

根據以上數學認知水平分析框架，對兩版教材平面向量的習題進行統計分析，具體如表4所示：

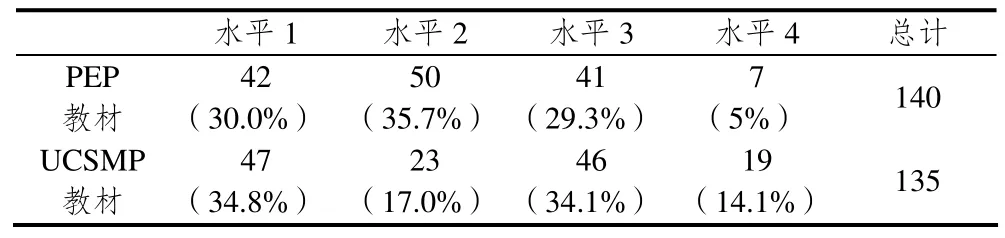
表4 兩版教材“平面向量”習題認知水平比較

從上表可知，兩版教材習題認知水平分布有顯著差異（χ2（3, N=275）=16.01，p<0.01）．水平1：計算——操作性記憶水平兩版教材題目數量所占比例相似，說明兩版教材的習題與例題匹配程度較高，學生可以參照例題、模仿例題進行解答．水平2：概念——概念性記憶水平的題目，PEP教材的題目要比UCSMP教材高18.7%．把水平1和水平2的題目合計，PEP教材中記憶水平（較低認知水平）的習題占65.7%，UCSMP教材記憶水平的習題占41.8%，比PEP教材低23.9%．水平3：領會——說明性理解水平的題目，UCSMP教材要比UCSMP教材高4.8%．水平4：分析——探究性理解水平的題目比例相差較大，UCSMP教材要比UCSMP教材高7.1%．水平3和水平4題目合計，PEP教材中理解水平（較高認知水平）的習題比UCSMP教材低23.9%．整體來看，PEP教材記憶水平的習題明顯多于UCSMP教材，主要是PEP教材水平2的習題明顯多于UCSMP教材，水平4的習題明顯少于UCSMP教材．

3.5 習題難度

以下對兩版教材平面向量部分的習題難度進行分析，為此，先根據表1中的水平劃分，對兩版教材中的習題逐一進行鑒定，并利用公式（*）計算每個難度因素的加權平均，其結果如表5所示．

由統計數據可知，在五個因素方面兩版教材具有顯著性差異（χ2（4, N=17）=15.56，p<0.01），具體分析如下：

（1）探究因素方面，兩版教材具有顯著性差異（χ2（2, N=275）=9.231，p<0.01）．PEP較注重“識記”，所占比例高達41.4%，比UCSMP教材高12.5%，體現了PEP教材抓基礎的特性，UCSMP教材卻更專注于“理解”和“探究”層次，“理解”層次所占比例要比PEP教材高3.5%，“探究”層次所占比例要比PEP教材高9%．另外，兩版教材的加權平均之后的難度值也相差0.21，由于UCSMP教材知識呈現以問題為載體，以問題解決為導向，因此習題中探究因素難度相比于PEP教材要大一些．

（2）背景因素方面，兩版教材具有顯著性差異（χ2（3, N=275）=33.022，p<0.001）．PEP教材中沒有實際背景的例習題要比UCSMP教材高出13.7%，而PEP教材涉及“個人生活”的習題占2.8%，UCSMP教材中涉及這方面的習題占9.6%，另外，UCSMP教材在涉及“公共常識”和“科學情境”的習題所占比例也大于PEP教材．由此可見，UCSMP教材中的習題更關注與學生的個人生活和公共生活方面的聯系，而PEP教材在這方面相對來說比較薄弱．

（3）運算因素方面，兩版教材差異不顯著（χ2（3, N=275）=1.098，p>0.5）．學生運算能力的培養主要體現在“簡單符號運算”水平，其中“復雜符號運算”水平層次，兩版教材的習題所占比例均比較低，分別為10.0%、14.1%，相對來說UCSMP教材中在復雜符號運算水平要高4.1%，其中很大一部分原因在于復習題中涉及了之前所學的知識．兩版教材運算因素方面的難度水平相差不大，這也說明兩版教材注重的都是基本運算的掌握，而弱化了對復雜運算的要求．

（4）推理因素方面，兩版教材差異不顯著（χ2（3, N=275）=2.454，p>0.25）．占比例較多的都是“無推理”水平，PEP教材所占比例為55.7%，UCSMP教材所占比例為46.7%．一方面是因為“平面向量”知識學生剛接觸，所以涉及到的“復雜推理”并不是很多；另一方面是兩版教材當中計算題和作圖題多一些，導致無推理題占的比例相對多一些．相對UCSMP教材來說，PEP教材中的習題在推理方面明顯比UCSMP教材的要簡單一些．主要是UCSMP教材比較注重知識的探究應用以及學生的數學能力的培養，特別是學生解決數學問題的能力，所以設置較多的“探索題”和“推理題”．

（5）知識含量方面，兩版教材具有顯著性差異（χ2（2, N=275）=6.022，p<0.05）．兩版教材均在“單個知識點”方面所占比例最高，其次是“兩個知識點”方面．由于“平面向量”的知識學生剛接觸，PEP教材更多的是落實基礎性原則，所以在這方面的難度要略小于UCSMP教材．UCSMP教材在這方面難度更大主要是因為其教材每章節后面的“復習類題”當中的題目綜合性都比較強，這些題都是對前面所學內容的鞏固和應用，有時還會與本小節知識綜合考查學生的掌握程度．

總體來說，UCSMP教材難度要大于PEP教材，部分習題難度較大，綜合性強，需要學生具有良好的基礎和較強的數學思維能力．而PEP教材在習題方面堅持以基礎題為主、中檔題為輔、適當涉及難度較大的綜合題和開放題，在保證問題數量的同時更要保證問題的質量．

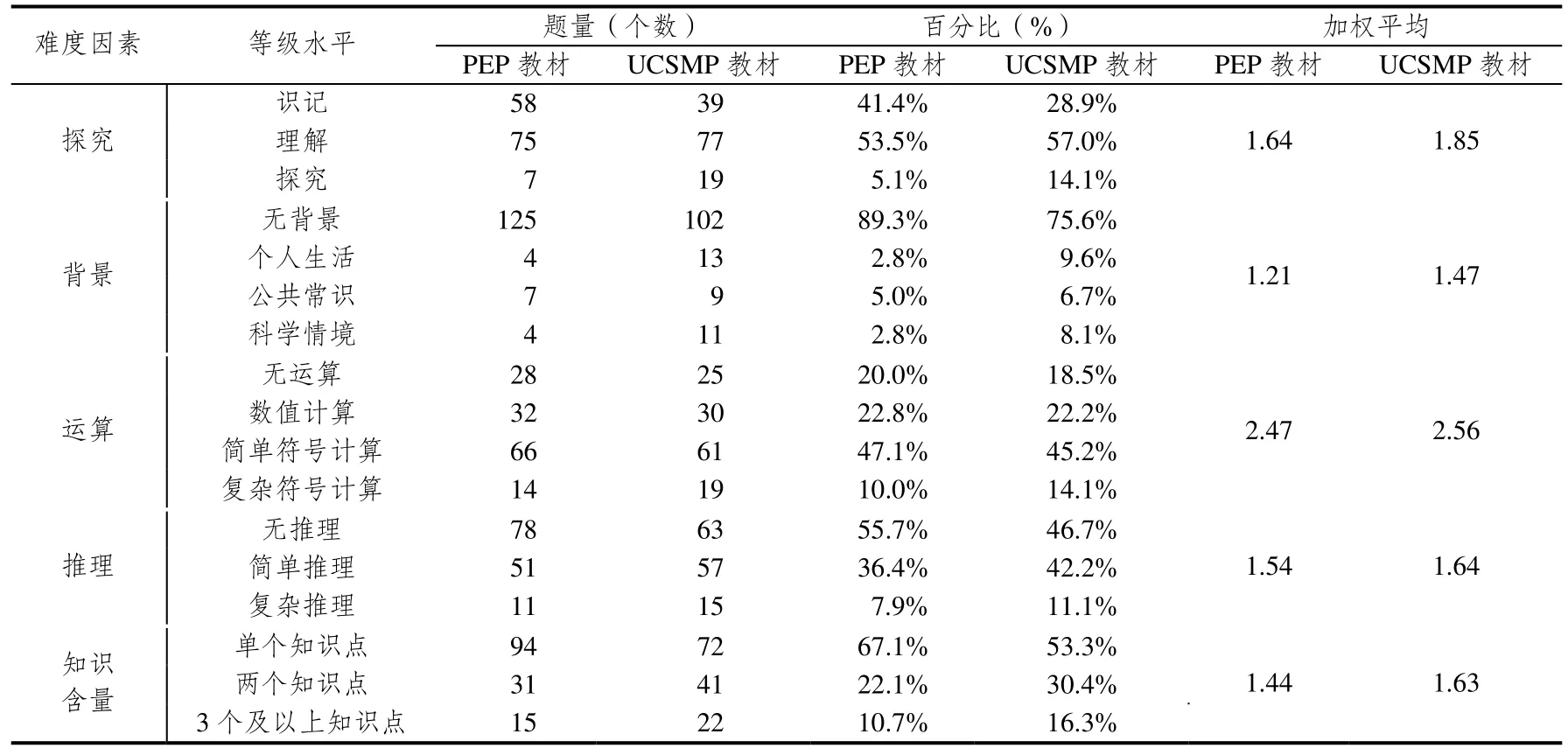
表5 習題難度的比較

4 啟 示

4.1 適當豐富習題呈現方式

習題既是知識的應用，又是知識和能力的再生．習題的設置在很大程度上會影響學生對數學知識的理解及其數學思維的形成過程[9]．PEP教材雖然對習題進行了分層次處理，但沒有根據不同的知識技能目標，進行更加細致具體的分層處理．UCSMP教材的節習題分為“鞏固題”、“應用題”、“復習題”、“探索題”等，對章復習題又以“技能”、“性質”、“應用”、“表達”4個方面分層次呈現，具有較完善的習題呈現方式，還根據各個層次的不同目標具體分配數量不同的習題．在教材編寫中，中國教材應該結合向量知識內容的特點，在保持層次性、重基礎等特色的同時，可參考UCSMP教材當中的習題呈現方式，根據不同的目標對習題更加細化分層，在節習題的設置上盡量涵蓋知識技能、理解應用、鞏固復習、探究拓展等目標的習題，增加習題的層次感和目的性．

4.2 提高較高認知水平習題比例增加探索性和開放性習題

根據以上研究發現，PEP教材安排了較多處于水平2——概念性記憶水平的題目，說明中國教材對主要概念、公式、定理等給予了充分重視，但UCSMP教材較高認知水平（水平3和水平4）的習題比例要遠多于PEP教材，習題形式也更豐富．水平3和水平4的習題要求學生在掌握概念、定理等知識的基礎上解決一些更復雜的問題，尤其是水平4——探究性理解水平的習題，學生需要根據不同的問題情境，創造性地解決一些非常規的問題．PEP教材需要在注重雙基、重視概念練習的前提下，學習借鑒UCSMP教材習題重視較高數學認知水平的培養，降低與例題形式完全相同、直接模仿例題解答的練習題比例，提高較高認知水平練習題，重視向量知識與其他數學領域知識聯系的做法，設置多樣化的習題，給學生提供一些非常規問題、開放題（結論開放或過程開放）、探索題等．由于“探索題”和“開放題”不一定有唯一的解法和結論，這就有助于培養學生的觀察、分析、綜合、類比、歸納、猜想等綜合解決問題的能力，數學教材中設置這樣一些習題就能夠更有效地引導和組織學生在經歷觀察、實驗、比較、分析、抽象概況等活動中，在相互合作交流中，對現實生活中蘊含的數學模式進行思考和交流，不斷提高學生用數學解決實際問題的能力，培養學生的創新能力和提出猜想、構造模型、推理證明并一般化等高水平數學能力[7]．

4.3 注重習題背景的多樣化緊密聯系生活實際

《普通高中數學課程標準（實驗）》指出：高中數學課程應力求使學生體驗數學在解決實際問題中的作用、數學與日常生活及其他學科的聯系，促進學生逐步形成和發展數學應用意識并提高實踐能力．新課程理念強調要把數學與現實生活相聯系，特別是與學生的個人生活相聯系，幫助學生學會“有用的數學”[9]．相對來說，PEP教材習題的選材與現實生活聯系的比較少，習題基本上都是純數學問題，較少有生活情景．而UCSMP教材中的習題背景涉及科學、經濟、物理、生物、化學、營養學等各個學科內容的相關知識，而且注重與學生的實際生活經驗相聯系．空洞的數字符號是不會容易讓學生產生興趣的，在教材編寫中應盡量讓習題選材密切聯系生活實際，特別是重視聯系學生個人的生活實際，創設更多的與學生息息相關的問題情境．設計富有挑戰性和趣味性的活動，使學生有更多的機會從周圍熟悉的事物中學習數學和理解數學，在認識、學習和應用數學知識的過程中，感受數學與生活實際的密切聯系．盡管PEP教材將平面向量的應用及與其他章節或學科的交叉部分置于同一節中，統一向學生介紹，這些應用涉及的更多是與物理相關的問題，但這遠遠不夠[10]．

總之，對比中美高中數學教材中的習題，可以發現美國數學教育中許多新的理念已經滲透到UCSMP教材中．中國數學教材的編寫應當認真研究這些教材的特色、特點，將美國成功的做法吸收到新教材中．當然，這種吸收不是簡單的抄襲，而是合理的吸收[11]．

[1] 孫曉天．近年來我國中小學數學教材建設述要[J]．數學教育學報，2008，17（4）：6-10．

[2] 葉立軍，王曉楠．中美高中數學教材比較研究[J]．數學教育學報，2012，21（2）：49-52．

[3] 王申懷．美國UCSMP教材（第六冊）介紹[J]．數學教育學報，1997，6（1）：66-70．

[4] 章建躍．普通高中課程標準實驗教材數學（選修2-2）[M]．北京：人民教育出版社，2007．

[5] UCSMP. Precalculus and Discrete Mathematics [M]. Chicago: The McGraw Hill Companies, 2010．

[6] 沈蘭，鄭潤洲．變革的見證：顧泠沅與青浦教學實驗年[M]．上海：上海教育出版社，2008．

[7] 高文君，鮑建生．中美教材習題的數學認知水平比較[J]．數學教育學報，2009，18（4）：57-60．

[8] 鮑建生．中英兩國初中數學期望課程綜合難度的比較[J]．全球教育展望，2002，（9）：48-52．

[9] 張笑謙，胡典順．中澳高中數學教材的比較及啟示[J]．數學教育學報，2013，22（2）：71-75．

[10] 張笑謙，胡典順．澳大利亞VCE課程與PEP高中數學教材平面向量章節的比較與思考[J]．數學通報，2013，（10）：22-27．

[11] 李善良．論中小學數學教材編寫的基本原則[J]．數學教育學報，2007，16（1）：70-73．

Comparative Study on Exercises of Chinese and American Mathematical Teaching Materials——A Case Study of Plane Vector Chapters from Chinese PEP Edition High School and American UCSMP Edition Teaching Materials

LIN Dan, HU Dian-shun
(School of Mathematics and Statistics, Central China Normal University, Hubei Wuhan 430079, China)

The reconstruction of teaching materials is an important mark of a new round of China’s reform of the mathematical curriculum, which also concretely represents the requirement and principle of the reform. By contrast of exercises of plane vector chapters from Chinese PEP edition high school and American UCSMP edition teaching materials, it can be found that the exercises from UCSMP edition textbooks are represented in various ways and redacted in different levels, are more closely connected to life and the cultivation of higher cognitive level, more open and thought-provoking, whereas are also more difficult. While the exercises from Chinese PEP edition high school textbooks are abundant in types, but not abundant in higher cognitive level, which makes them better from the perspective of difficulty. However, it shows an inadequacy of open and thought-provoking questions. In the compiling of teaching materials, PEP may consider to enrich the ways of presentation, improve the proportion of exercises of the higher cognitive level, add more exploratory questions, pay attention to the diversity of background of exercises and strengthen their connection to life.

contrast of mathematical teaching materials; plane vector; exercises; enlightenment

G40-059.3

：A

：1004–9894（2015）03–0063–05

[責任編校：張楠]

2015–01–20

湖北省教學研究項目——數學師范生拔尖創新人才培養的理論與實踐（2013090）；中央高校基本科研業務費專項資金資助——數學問題提出與數學教育改革：跨國比較研究（CCNU13F021）；華中師范大學研究生教學改革研究項目——免費師范生攻讀教育碩士培養模式的改革研究與實踐（2013JG18）；華中師范大學教師教育學院研究專項資助（2012JS07）；湖北省教育科學“十二五”規劃2013年度立項課題——數學問題提出與數學教育改革：跨國比較研究（2013B015）

林丹（1991—），女，江西贛州人，碩士，主要從事數學課程和教學論的研究．胡典順為本文通訊作者．