三種平面坐標轉換方法及其精度分析
馬生龍 申成鋒 張世貝
(青海省有色地勘局地質礦產勘查院,青海 西寧 810007)
·測量·
三種平面坐標轉換方法及其精度分析
馬生龍 申成鋒 張世貝
(青海省有色地勘局地質礦產勘查院,青海 西寧 810007)
以青海省海西州某縣礦業權核查數據為例,采用四參數模型、六參數模型和二次多項式擬合進行平面坐標轉換,在地形起伏較大地區對比分析了不同公共點密度和分布情況下不同模型的轉換精度,歸納總結出三種模型的特性,為實際的工程應用提供參考。
平面坐標轉換,轉換模型,公共點選取,轉換精度
0 引言
目前,我國采用的坐標系主要有1954北京坐標系、1980西安坐標系、2000國家大地坐標系(CGCS2000)以及各種地方獨立坐標系。在實際工程應用中,不同坐標系下的成果常常需要進行統一,從而涉及到坐標轉換的問題。自20世紀60年代以來,各國大地測量學者經過大量研究,提出了多種坐標轉換模型及多種解算方法。從坐標系間的關系出發,提出了相似變換模型,如三參數[1]、四參數[2]、七參數模型等,通過數值逼近,提出了多項式轉換模型[3]、格網插值法[4]等,之后又提出相似變換結合回歸逼近、相似變換結合插值法、基于總體最小二乘[5]和基于人工神經網絡[6]等坐標轉換方法。
常用的平面坐標轉換方法有四參數模型、六參數模型和二次多項式擬合等,這些模型對于不同工程項目的坐標轉換各有優缺點,為了更好地分析各模型的特點和適用性,本文在文獻[6]的基礎上,以青海省海西州某縣礦業權核查中12個公共點(均包含1954北京坐標系和1980西安坐標系)為例,進一步分析地形起伏較大地區公共點密度及分布情況對三種模型轉換精度的影響。
1 模型及其參數求解
1.1 四參數模型
四參數模型[2]是一種相似變換,其計算公式為:
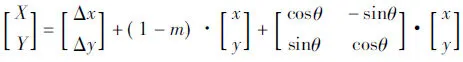
(1)
其中,Δx,Δy,θ,m分別為平面上的平移、旋轉、尺度參數。當有兩個以上轉換公共點時,將此模型轉換為線性模型用最小二乘求解:
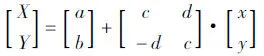
(2)
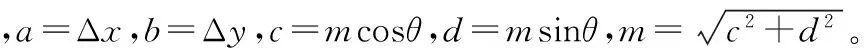
1.2 六參數模型
六參數模型[7]是一種仿射變換,在任意兩個平面坐標間的六參數仿射變換,可以用如下公式:
(3)
其中,Δx,Δy均為平移參數;α,β均為旋轉參數;λx,λy均為比例因子。顯然,要求解六個轉換參數,至少需要三個公共點的坐標。當有三個以上轉換公共點時,可用最小二乘求解轉換參數。根據a0,a1,a2,b0,b1,b2可以計算出六個轉換參數:Δx,Δy平移參數,α,β旋轉參數,λx,λy尺度因子。
1.3 二次多項式擬合
二次多項式擬合[3]是多項式變換中的一種,其計算公式如下:
(4)
其中,a0,a1,a2,a3,a4,a5,b0,b1,b2,b3,b4,b5均為轉換參數,當轉換點個數多于6個時,可以通過最小二乘法結合線性回歸原理求解轉換參數。
2 算例分析
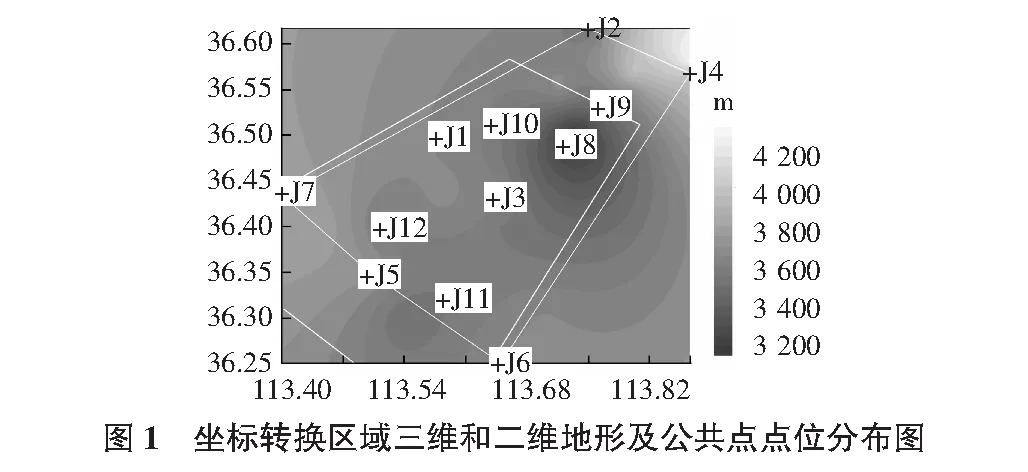
相比于文獻[7]選取的小范圍平坦地區的研究區域,本文采用青海省海西州某縣較大范圍的礦業權核查坐標數據進行坐標轉換,面積約780 km2(圖1白色線范圍),公共點之間的最大距離(J2和J6)約40 km,區域內有12個公共點。從圖1中可以看出,區域內地形起伏較大,平均海拔約為3 600 m,公共點高差最大約1 000 m(最高點J4和最低點J8),且公共點的分布不均勻。
由于二次多項式擬合需要至少6個公共點才能求解轉換參數,因此,為了研究公共點密度和分布對轉換精度的影響,本文給出了四種組合方案用于求解不同模型的轉換參數(見表1),其余點作為檢驗點檢驗轉換的精度,采用最大絕對偏差、坐標分量中誤差及點位中誤差進行精度評定,其計算方法如下:
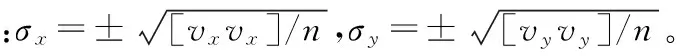
當計算內符合精度時,n為轉換點個數;計算外符合精度時,n為檢驗點個數。
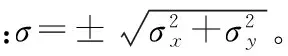

表1 四種組合方案所包含的公共點
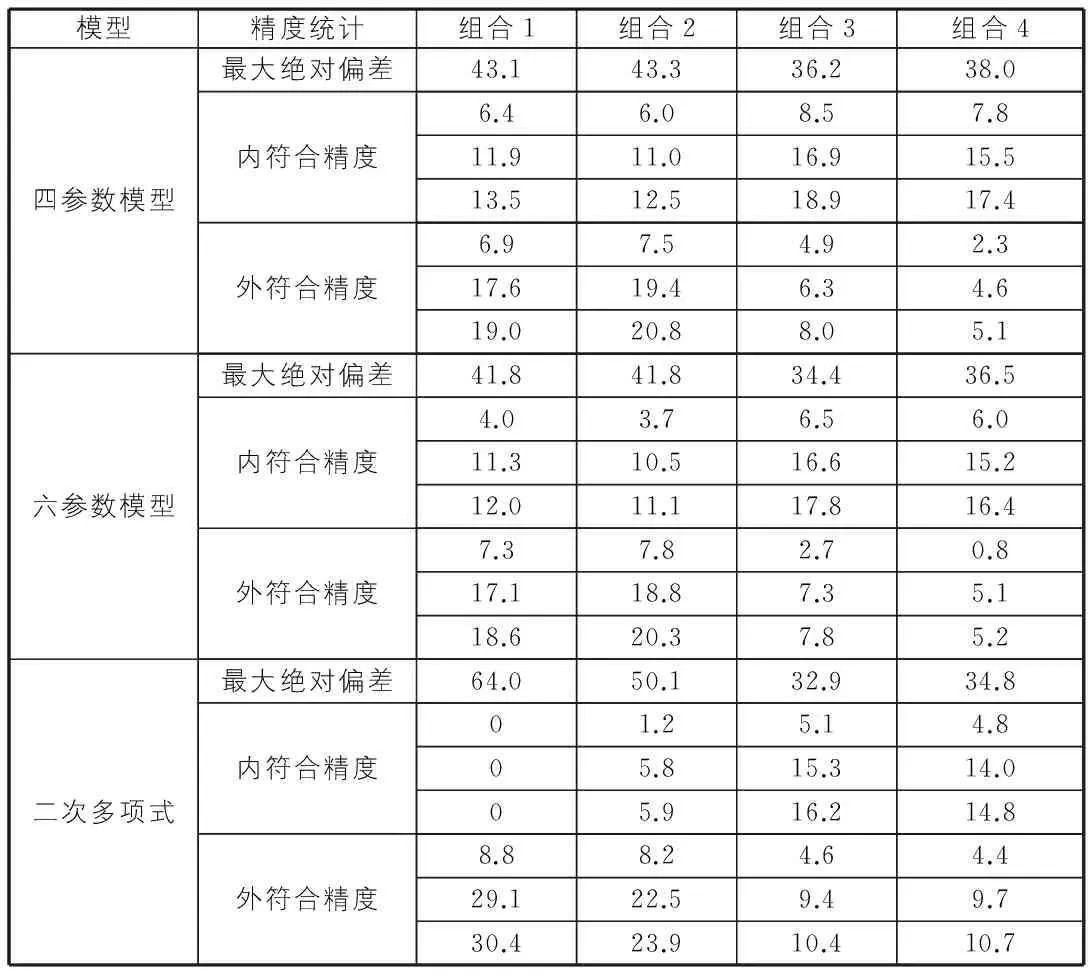
表2 不同模型采用不同組合方案的坐標轉換精度統計
從表2中最大絕對偏差可以看出,總體上增加轉換點的個數可以提高坐標轉換的精度,特別是將J8號(區域內最低點)點用于求解轉換參數時,三種模型的最大絕對偏差均有了明顯的減小,減小最為明顯(達到17.2 mm)的為二次多項式擬合。由于四參數模型和六參數模型未顧及控制網的局部變形,將J8號點納入轉換參數的求解時其精度變化不是很明顯,而六參數模型由于采用了兩個尺度因子,其精度略高于四參數模型。比較組合1和組合2可以看出,當選取區域邊界上的公共點求解轉換參數時,增加區域內的轉換點個數對于四參數和六參數模型的轉換精度幾乎沒有改善,而二次多項式擬合的坐標轉換精度則有明顯的提高。比較組合3和組合4兩種方案可以看出,增加轉換點的個數不僅沒有提高三種模型的轉換精度,其最大絕對偏差反而變大。從最大絕對偏差以及內外符合精度相當的角度綜合來看,二次多項式擬合采用組合3方案獲得的坐標轉換效果最佳。
3 結語
本文在地形起伏較大地區利用三種平面坐標轉換模型進行坐標轉換,結果表明:1)將區域內海拔較高和較低的公共點用于求解坐標轉換參數時,二次多項式擬合由于顧及控制網的局部變形,其坐標轉換精度有了明顯的提高,而四參數模型和六參數模型未顧及控制網的局部變形,二者的轉換精度沒有明顯改善;2)當用于求 解轉換參數的公共點的數量和分布到達一定程度時,增加公共點的個數并不一定能提高轉換的精度。因此,在地形起伏較大的地區使用二次多項式擬合進行坐標轉換時,除了選取區域邊界的公共點作為轉換點外,還需將區域內高程異常(高程明顯高出或低于區域平均高程)的點納入到轉換參數的求解中,以減少控制網局部變形的影響。
[1] 符建波,高帥華.三參數坐標轉換模型轉換精度的研究[J].礦山測量,2014(5):54-56.
[2] 劉科利.北京54和西安80坐標系下的坐標轉換及精度分析在Excel中的實現[J].勘察科學技術,2008(5):24-27.
[3] 姜晨光.用線性回歸方法將GPS坐標轉為地方坐標[J].測繪科技通訊,1998(1):17-19.
[4] 施建平,楊華忠.克里金內插法實現坐標轉換的應用研究[J].海洋測繪,2010,30(4):30-32.
[5] 劉立龍,姚朝龍.LS和TLS在平面坐標轉換中的應用[J].測繪科學,2012,37(5):12-14.
[6] 宋 雷,胡伍生.基于神經網絡坐標差學習的GPS坐標轉換[J].測繪通報,2012(S1):29-31.
[7] 姚朝龍,劉立龍.幾種模型在平面坐標轉換中的應用[J].地理空間信息,2011,9(2):64-65.
[8] Ronggang Guo.Systemtical Analysis of the Transformation Procedures in Baden-Württemberg with Least Sqrares and Total Least Squares Methods[D].Stuttgart:University of Stuttgart,2007.
Three kinds of plane coordinate conversion methods and their precision analysis
Ma Shenglong Shen Chengfeng Zhang Shibei
(GeologyandMineralResourcesSurveyInstitute,QinghaiNonferrousGeologicalProspectingBureau,Xining810007,China)
Taking a mining right inspection data in Qinghai Haixi as an example, this paper made plane coordinate transformation using four parameters model, six parameters model and secondary polynomial fitting, under the undulating topography region comparative analyzed the different public point density and different models transformation precision under different distribution situation, summed up the characteristics of three models, provided reference for actual engineering application.
plane coordinate transformation, transformation model, public point selection, conversion accuracy
2015-03-08
馬生龍(1988- ),男,助理工程師; 申成鋒(1990- ),男,助理工程師; 張世貝(1980- ),男,助理工程師
1009-6825(2015)14-0204-02
TU198
A

