股票價格穩定性的非參數平滑估計

王 俏，王文舉

(首都經濟貿易大學 經濟學院，北京 100070)

股票價格穩定性的非參數平滑估計

王 俏，王文舉

(首都經濟貿易大學 經濟學院，北京 100070)

股票的優質性主要由股票價格的穩定性來決定。通過建立條件風險函數非參數平滑估計的估計方法，證明條件風險函數平滑后的非參數估計值具有一致性和漸進正態性，并將此方法擴展到了截尾數據中。通過蒙特卡羅模擬表明條件風險函數平滑后的非參數估計值在非截尾數據以及截尾數據中的有限樣本行為都要優于非平滑的估計值。實證分析中用截尾數據條件風險函數非參數平滑估計方法非參數估計中國14大行業股票價格的穩定性,發現房地產行業的股票價格最不穩定，建筑材料行業的股票價格表現最穩定。

條件風險函數；非參數平滑估計；截尾數據

風險函數是研究事件發生時間的最常用的計量方法。風險函數最早用于研究人類壽命、人類壽命的分布特征以及人類壽命的影響因素等。隨著計量經濟學的發展，風險函數現在主要用于研究事件的發生時間，例如勞動者失業的時間、企業破產的時間、政策生效的時間等。對風險函數進行參數和半參數估計都需要假設風險函數的函數形式，但是函數形式的假設條件是無法被證明的，這對于實證分析有很大的局限性。對風險函數進行非參數估計的研究已有很多：如坦納和王(Tanner & Wang，1983)[1]、坦納(Tanner，1983)[2]、辛格普瓦拉和黃(Singpurwalla & Wong，1983)[3]、楊德爾(Yandell，1983)[4]、塞勒(Thaler，1984)[5]、坦納和黃(Tanner & Wong，1984)[6]、謝弗(Schafer，1985)[7]、穆勒和王(Muller & Wang，1994)[8]、岡薩雷斯、曹和馬榮(Gonzalez，Cao & Marron，1996)[9]、霍爾等(Hall et al,2001)[10]。

條件風險函數研究某些因素變量對事件發生時間的影響，例如：哪些因素影響了勞動者失業時間的長短以及如何影響，哪些因素影響了財政政策或者貨幣政策的滯后效應以及如何影響，因此條件風險函數有很強的實證分析的意義。可以通過條件風險函數的非參數估計方法來非參數估計股票價格的穩定性，其具體定義如下：

(1)

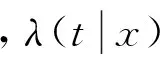
(2)

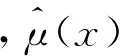
(3)

在他們的非參數估計中，條件累計密度函數是非平滑的核估計值，其有限樣本行為沒有平滑后的核估計值有限樣本行為穩健。因此，本文用平滑后的條件累計密度函數核估計方法對條件風險函數進行非參數估計，并將此估計方法擴展到截尾數據中。通過蒙特卡羅模擬表明：條件風險函數平滑后的非參數估計值的有限樣本行為確實比非平滑估計值的有限樣本行為好。

本文的結構安排如下：第一部分提出條件風險函數非參數平滑估計方法，并證明平滑后的估計值具有一致性和漸進正態性；第二部分將此估計方法擴展到截尾數據中，證明對于截尾數據，平滑后的估計值仍然具有一致性和漸進正態性；第三部分通過蒙特卡洛模擬進行比較表明：條件風險函數非參數平滑估計值在非截尾數據以及截尾數據中都比非平滑估計值的有限樣本行為好；第四部分對于截尾數據應用條件風險函數非參數平滑估計方法研究中國股票價格的穩健表現；第五部分給出結論。

一、非參數平滑估計方法

本文的條件風險函數的非參數估計值為：

(4)

使用下面的平滑條件累計密度函數的核估計值來對條件風險函數進行非參數估計：

(5)

其中，G(·) 是核累計密度函數，h0是核累計密度函數的窗寬。

李和拉親(Li&Racine，2008)[13]證明了平滑條件累計密度函數的核估計值(5)的一致性和漸進正態性。以下證明條件風險函數非參數平滑估計值(4)的一致性和漸進正態性。

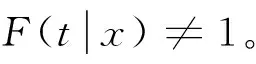
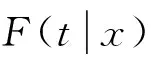
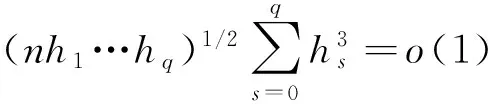
假設4：(Xi,Ti) 是嚴格的平穩過程，與(x,t)有同樣的邊際分布函數。

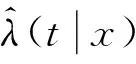
定理1：在假設條件1-4成立的條件下，有：

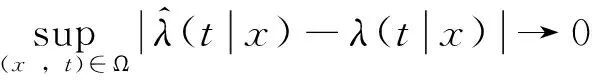
證明：證明過程分兩步。

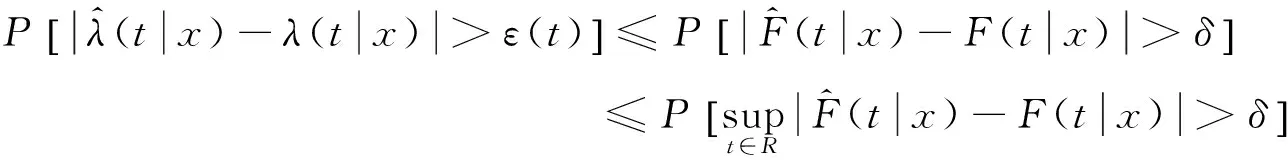
(6)

根據波萊爾-坎泰利(Borel-Cantelli)引理[14]，有：

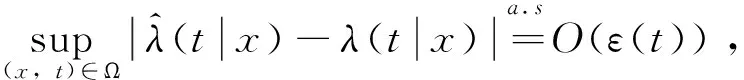
第二步：定義η=Dα(x)+(nh1…hq)-1/2Vα(x)v,

(7)

如果設定:

(8)

其中，Φ(v) 是標準正態分布函數。那么可以得到:

(9)

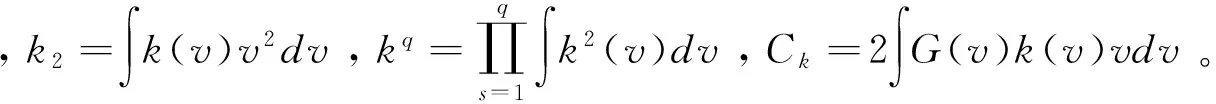
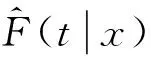
可以得到:

(10)

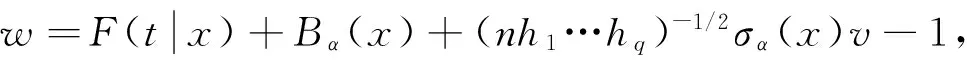
(11)

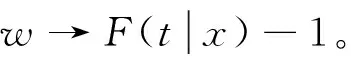
(12)

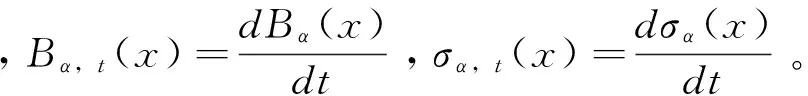
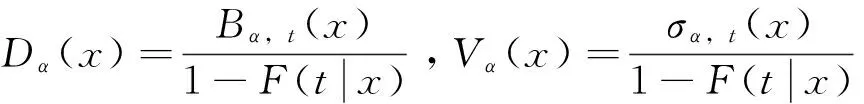
(13)

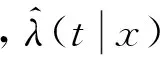
(14)

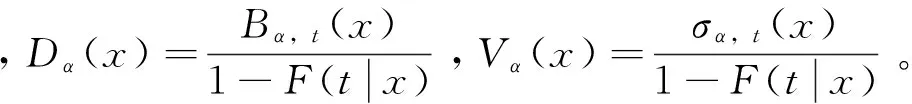
定理1表明條件風險函數非參數平滑估計值的收斂速度與一般的非參數估計值的收斂速度相同，條件風險函數非參數平滑估計值具有一致性和漸進正態性。

二、對截尾數據的擴展

大部分實證數據都存在截尾數據的情況，事件發生的時間Yi不是全部可以觀察到的，因此本部分將條件風險函數非參數平滑估計方法擴展到截尾數據中，以提高平滑估計方法實證分析的適用性。本文假設截尾時間為Ci。因此Yi=min(Ti,Ci)并且δi=1(Ti≤Ci) ，其中Ti是可以觀察到的事件發生時間。

截尾數據條件風險函數定義為：

(15)

(16)

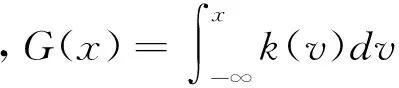
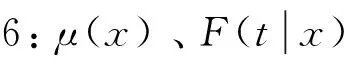
假設7：(Xi,Ti,Ci,δi) 是嚴格的平穩過程，與(x,t,c,δ)有同樣的邊際分布函數。

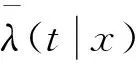
證明：

(17)

(18)

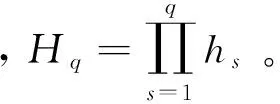
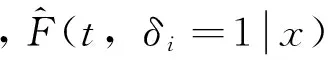
(19)

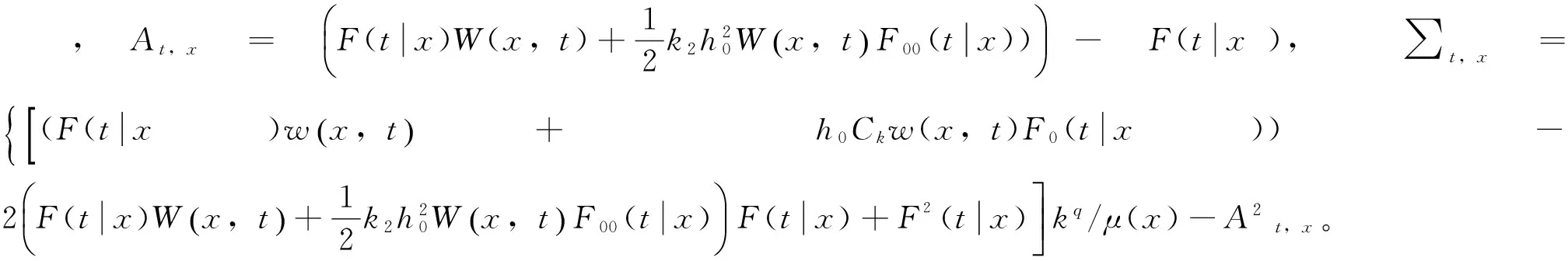
定理2：在假設條件5—假設7成立的條件下，有:

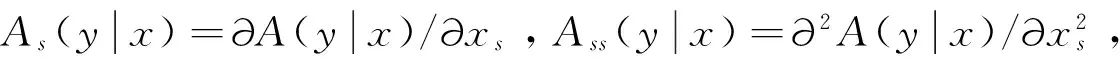
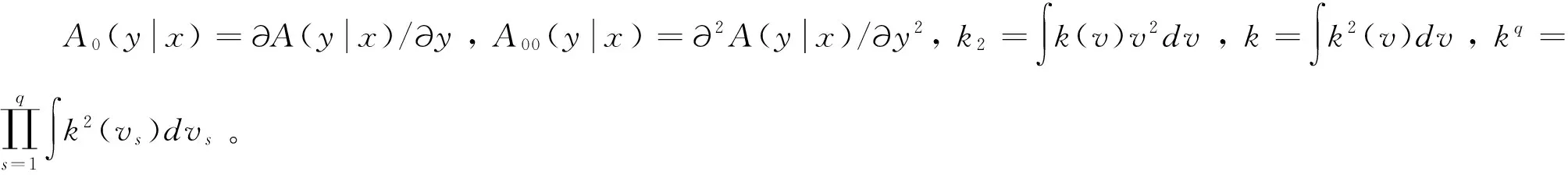
(20)

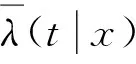
(21)

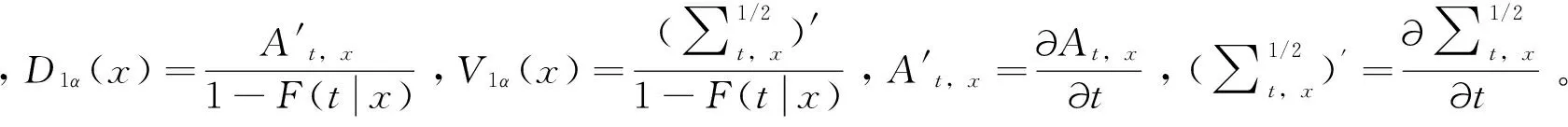
定理2表明在存在截尾數據時，條件風險函數非參數平滑估計值仍然具有一致性和漸進正態性。表明條件風險函數非參數平滑估計方法可以擴展到截尾數據中，提高了此估計方法的實用性。

三、蒙特卡羅模擬比較分析

本部分進行蒙特卡羅模擬，來比較條件風險函數非參數平滑估計值與非平滑估計值在非截尾數據以及截尾數據中的有限樣本行為。

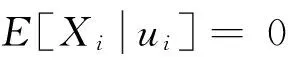
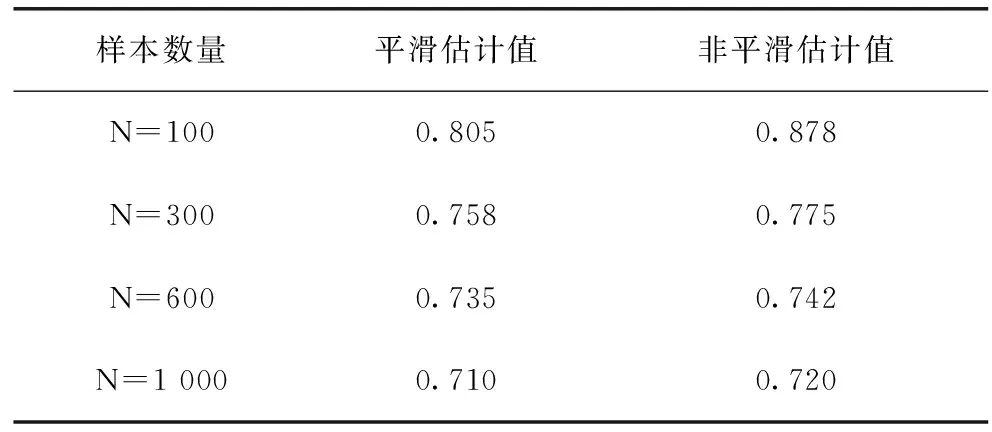
表1 非截尾數據模擬比較結果

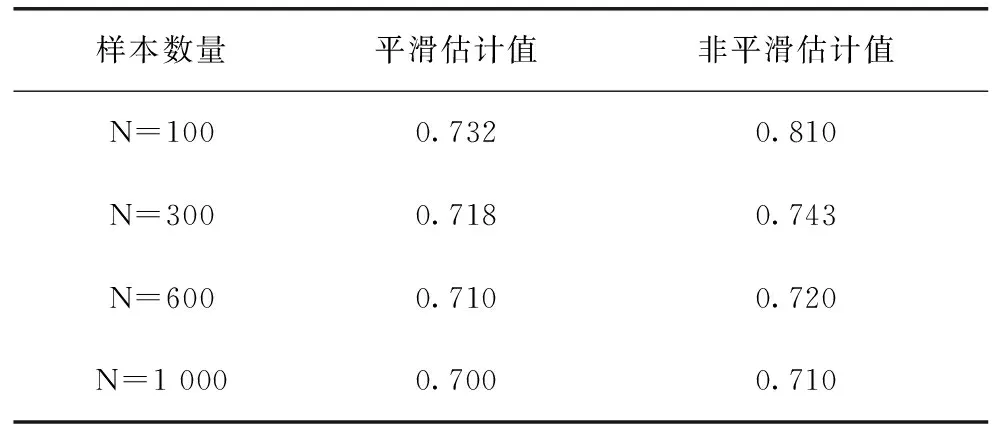
表2 截尾數據的模擬比較結果

模擬結果表明：無論是在非截尾數據中還是在截尾數據中，隨著樣本量的增加，平滑估計值與非平滑估計值的有限樣本行為都變得越來越好，但是，無論樣本量多大，條件風險函數非參數平滑估計值的有限樣本行為都要優于非平滑的估計值。因此，無論數據是截尾的還是非截尾的，平滑估計值的有限樣本行為都要優于非平滑的估計值。

四、中國股票價格穩定性分析

將截尾數據條件風險函數非參數平滑估計應用到中國滬深300指數的300個股票樣本上，研究這300個股票樣本的價格波動情況。根據岡薩雷斯等(Gonzalez et al,2008)[16]，定義第i支股票在第t期股票排名的變量zit為：

(22)

其中M為總共的股票樣本數，本文的數據來源于CCER中國經濟金融數據庫，由于數據獲得的限制，在300個股票樣本中只選取242支股票為研究對象，所以M=242，pit為第i支股票在第t期的價格。具體變量z的意義見岡薩雷斯等(2008)[16]的表1。定義第i支股票在第t期跳躍的變量Jit為：

(23)

由于本文選取的242支股票樣本的價格數據是2013年11月28日到2014年11月28日的日數據，所以定義股票排名的波動幅度為0.01，如果Jit=1，說明第i支股票的日波動幅度很大，股票排名下降或者提升的位置大于2，如果Jit=0，說明第i支股票的日波動幅度很小，股票價格穩定，股票排名下降或者提升的位置小于2。

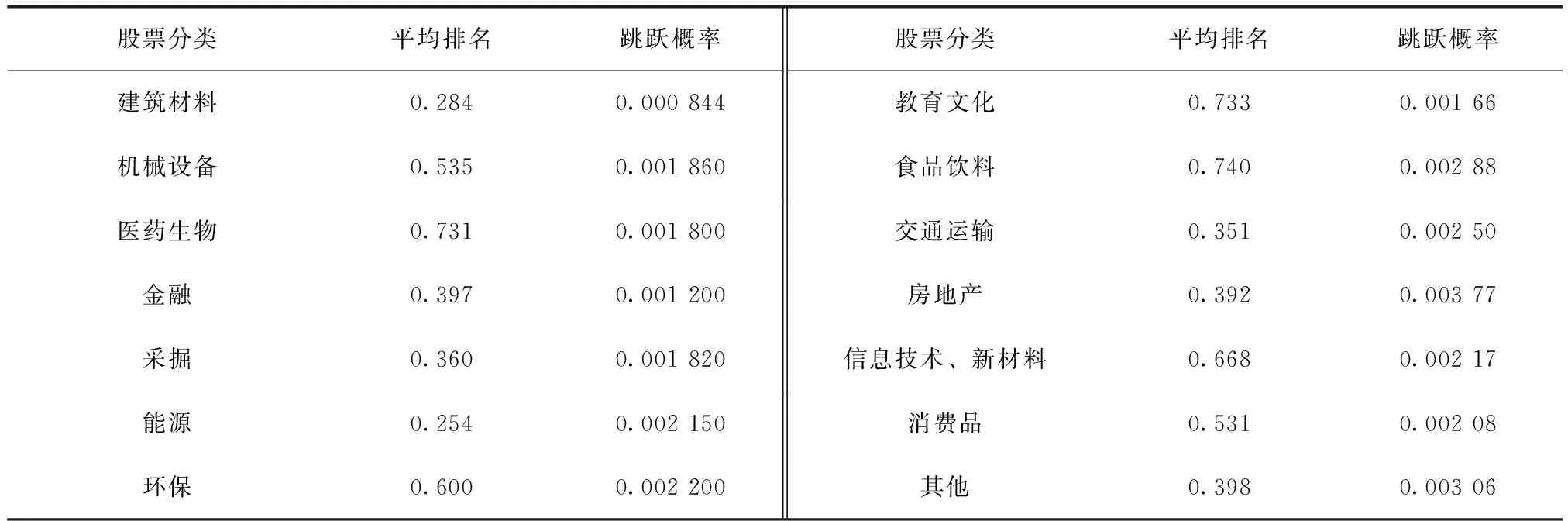
表3 股票的平均排名和跳躍概率

從表3的估計結果可知：跳躍概率最大的是房地產行業，跳躍概率最小的是建筑材料，平均排名最高的是食品飲料、教育文化和醫藥生物行業，平均排名最低的是建筑材料和能源行業。所以表現最好的兩個行業的股票是教育文化和醫藥生物行業，跳躍的概率都不大，靠前的排名比較穩定，而食品飲料的跳躍概率稍微偏大，股票價格靠前的排名不是很穩定。表現最不好的兩個行業的股票是建筑材料和能源行業，建筑材料跳躍的概率非常小，股票排名穩定靠后，能源行業跳躍的概率稍微偏大，最低的排名并不穩定。房地產是股票價格排名最不穩定的行業。

五、主要結論

本文給出了條件風險函數非參數平滑估計方法，通過證明、模擬和實證分析，得到：

1.條件風險函數非參數平滑估計值具有一致性和漸進正態性。

2.對于截尾數據，條件風險函數非參數平滑估計值仍然具有一致性和漸進正態性。

3.蒙特卡羅模擬結果顯示條件風險函數非參數平滑估計值在非截尾數據以及截尾數據中的有限樣本行為都要優于非平滑估計值。

4.用截尾數據條件風險函數非參數平滑估計方法研究中國滬深300股票的估計結果表明：教育文化和醫藥生物行業的股票表現最好，排名靠前，比較穩定；建筑材料和能源的股票表現最不好，排名靠后；房地產是排名最不穩定的行業。

[1]TANNER M A,WANG W H.The Estimation of Hazard Function From Randomly Censored Data by the Kernel Method[J].The Annuals of Statistics，1983,11(3):989-993.

[2]TANNER M A.A Note on the Variable Kernel Estimator of the Hazard Function From Randomly Censored Data [J].The Annuals of Statistics，1983,11(3):994-998.

[3]SINGPURWALLA N D,WONG M Y.Kernal Estimation of Failure-rate Function and Density Estimation:An analogy[J].Journal of the American Statistics Association，1983,78(382):478-481.

[4]YANDELL B S.Nonparametric Inference for Rates with Censored Survival Data[J].The Annuals of Statistics，1983,11(4):1119-1135.

[5]THALER H T.Nonparametric Estimation of Hazard Ratio[J].Journal of the American Statistics Association，1984,79(386):290-293.

[6]TANNER M A,WONG M Y.Data-based Nonparametric Estimation of the Hazard Function with Application to Model Diagnostic and Exploratory Analysis [J].Journal of the American Statistics Association，1984.79(385):174-182.

[7]SCHAFER H.A Note on Data-Adaptive Kernel Estimation of the Hazard and Density Function in the Random Censorship Situation[J].The Annuals of Statistics，1985,13(2):818-820.

[8]MULLER H G,WANG J L.Hazard Rate Estimation under Random Censoring with Varying Kernels and Bandwidths[J].Biometrics，1994.50(1): 61-76.

[9]GONZALEZ-MANTEIGA W，CAO R,MARRON J S.Bootstrap Selection of the Smoothing Parameter in Nonparametric Hazard Rate Estimation[J].Journal of the American Statistics Association，1996,91(435):1130-1140.

[10]HALL P，HUANG L S，GIFFORD J A,et al.Nonparametric Estimation of Hazard Rate under the Constraint of Monotonicity[J].Journal of Computational and Graphical Statistics，2001,10(3):592-614.

[11]BERAN M.Nonparametric Regression with Randomly Censored Survival Data[Z].University of California，Berkeley,1981.

[12]SPIERDIJK L.Nonparametric Conditional Hazard Rate Estimation:A local linear approach[Z].Working Paper，University of Twente,2005.

[13]LI Q,RACINE J S.Nonparametric Estimation of Conditional CDF and Quantile Functions with mixed Categorical and Continuous data[J].Journal of Business & Economic Statistics，2008,26(4):423-434.

[14]Durrett R.，2010，Probability:Theory and Examples[M].Cambridge University Press.

[15]HOROWITZ J L.A smoothed maximum score estimator for the binary response model[J].Econometrica，1992,60(3):505-531.

[16]GONAZLEZ RIVERA G，LEE T H,MISHRA S.Jumps in Cross-Sectional Rank and Expected Returns:A Mixture Model[J].Journal of Applied Econometrics，2008,23(5):585-606.

(責任編輯：姚望春)

Nonparametric Smoothed Estimation of Stability of Stock Price

WANG Qiao,WANG Wenju

(School of Economics,Capital University of Economics and Business,Beijing 100070,China)

The quality of a stock is mainly determined by its stability.Firstly,a nonparametric smoothed estimation of conditional hazard function is proposed.The consistency and asymptotic normality of the estimator and extend the kernel method to censored data are proved.The simulation study indicates that the smoothed estimator of conditional hazard function without or with censored data performs better than the non-smoothed estimator in finite samples.Secondly,the stability of 14 industries’ stock price is estimated with the smoothed method.The estimation result shows that the stock price of real estate is the least stable and the stock price of construction is the most stable.

conditional hazard function;smoothed nonparametric;censored data

2015-07-07

國家社會科學基金重大項目“中國碳市場成熟度、市場機制完善及環境監管政策研究”(14ZDA072)；北京市屬高等學校高層次人才引進與培養計劃“長城學者”資助項目“碳排放與博弈計量研究”(CIT&TCD20140321)

王俏(1987—)，女，首都經濟貿易大學經濟學院經濟學博士研究生；王文舉(1965—)，男，首都經濟貿易大學經濟學院教授，博士生導師。

O212

A

1008-2700(2015)06-0022-08