排除圖形干擾,尋求解題途徑
2015-06-12 10:04:52張志仁
中國校外教育(中旬) 2015年5期
張志仁

摘要:立體幾何中平常我們見到的幾何圖形一般都是常規(guī)放置的,對于涉及到的圖形的性質(zhì)在常規(guī)放置的圖形中學(xué)生都比較適應(yīng)。因而,解題過程一般情況下不會有多大的問題。但是,一旦圖形反常規(guī)放置形成干擾,那么對于空間圖形想象力較差的同學(xué)來說,他們就會覺得難以想象,原本會求解的問題會變得無從下手。以教學(xué)中遇到的兩例加以說明。
關(guān)鍵詞:立體幾何 圖形干擾 解題途徑
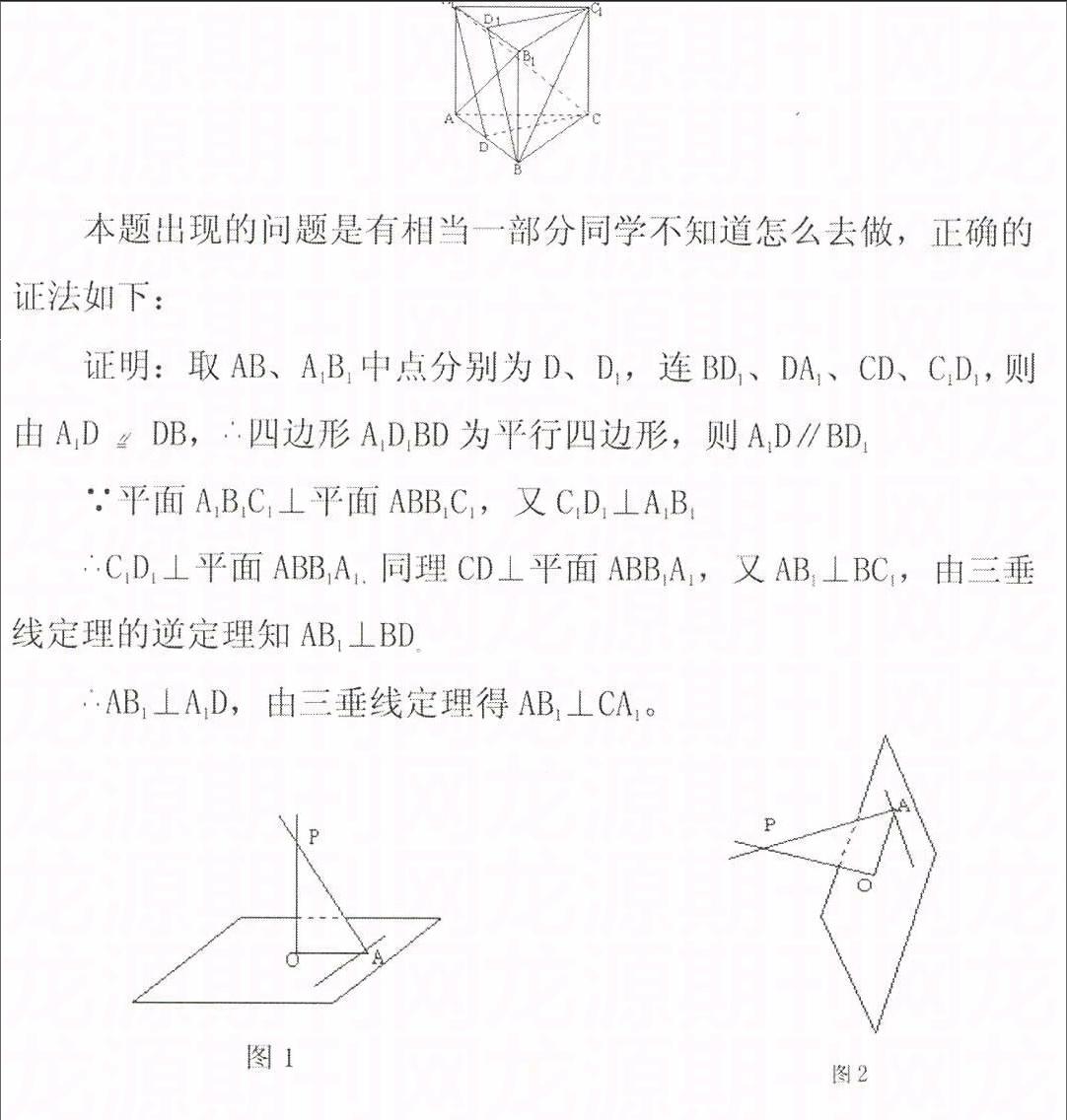
例1.在正三棱柱ABC—A1B1C1中,若AB1⊥BC1。求證:AB1⊥CA1。
不會證明的同學(xué)的問題是他們在三垂線定理及其逆定理的應(yīng)用中僅僅對基本圖形(1)相當(dāng)熟悉.但是當(dāng)圖形(1)在空間旋轉(zhuǎn)一下變成圖形(2)之后,就覺得生疏不理解造成的。
本題也可利用面面平行來證,可作BM⊥PC,連結(jié)DM,證明面BDM與面AGEF平行,從而得出結(jié)論。
針對這種情況,我們在立體幾何教學(xué)中應(yīng)注重培養(yǎng)學(xué)生的空間想象能力。這包括對空間圖形的觀察、分析、抽象能力;圖形與圖形之間的變換能力;注意進(jìn)行反常規(guī)圖形干擾的訓(xùn)練,以培養(yǎng)學(xué)生排除常規(guī)圖形的干擾能力。在近年的高考中也充分體現(xiàn)了這一點(diǎn)。例如,2000年高考理科第18題的第(3)問對于C—C1BD這個正三棱錐有些同學(xué)不會用,從而導(dǎo)致解答錯誤,就充分體現(xiàn)了圖形干擾可造成失誤。

