截斷總體最小二乘法在抑制地磁導航磁力儀隨機誤差方面的應用

王立輝，余 樂，梁冰冰，喬 楠

（1. 東南大學 儀器科學與工程學院 微慣性儀表與先進導航技術教育部重點實驗室，南京 210096；2. 空間物理重點實驗室，北京 100076）

截斷總體最小二乘法在抑制地磁導航磁力儀隨機誤差方面的應用

王立輝1，余 樂1，梁冰冰2，喬 楠1

（1. 東南大學 儀器科學與工程學院 微慣性儀表與先進導航技術教育部重點實驗室，南京 210096；2. 空間物理重點實驗室，北京 100076）

三軸磁力儀的隨機誤差補償技術是當前水下地磁導航領域的研究熱點。傳統(tǒng)上采用最小二乘法或其相關改進方法進行誤差修正，是基于假設隨機誤差為高斯分布或者沒有考慮到磁力儀觀測方程的病態(tài)問題。將總體最小二乘方法與正則化方法結合起來，提出一種截斷總體最小二乘法，來處理觀測方程兩邊都存在隨機誤差的病態(tài)問題。仿真結果表明，截斷總體二乘法能很好地抑制磁力儀測量中的病態(tài)影響，且將經(jīng)過截斷總體二乘法標定前后的殘差減小至10 nT以內。此外，比起最小二乘法補償和總體最小二乘法補償后的測量數(shù)據(jù)，經(jīng)過截斷總體最小二乘法補償后的測量數(shù)據(jù)更加接近真實值，達到了抑制隨機誤差的目的。

水下地磁導航；三軸磁力儀；病態(tài)問題；截斷總體最小二乘法；隨機誤差補償

地磁輔助導航系統(tǒng)具有隱蔽性好、信息量豐富等優(yōu)勢，是解決水下載體長航時、高精度、自主導航問題的有效途徑之一，成為一種重要的水下導航與定位方法[1-2]。磁場物理量的實時測量獲取在整個地磁輔助導航系統(tǒng)中有著舉足輕重的作用[3]。在實際測量過程中，由于存在干擾磁場、磁力儀自身精度誤差、地磁觀測不充分等因素，影響了磁力儀測量的準確性，需要對磁力儀進行誤差補償[4]。

在地磁導航磁力儀測量誤差補償方面，幾種磁力儀補償模型相繼被提出：非線性兩步法算法對磁力儀的輸出進行建模，引入中間變量，利用相關公式求得補償系數(shù)，可以減小計算量并無需提供初始值[5-6]；自適應最小二乘法（ALS）根據(jù)隨機誤差的標準方差自適應地給出一致的參數(shù)估計值，并且已經(jīng)運用到磁力儀導航中的傳感器標定補償問題中[7]；一種基于遞歸加權最小二乘（RWLS）算法的磁力儀誤差補償方法在每一步遞歸更新階段都避免了矩陣求逆的操作，使數(shù)值求解過程更加穩(wěn)定[8]；總體最小二乘（TLS）考慮了線性矩形方程兩端存在測量誤差，進一步提高了標定補償?shù)臏蚀_性[9]。

在航海測量過程中，三軸磁力儀在垂直方向上的測量分量受到了載體機動能力的限制，使得垂直方向的誤差參數(shù)無法被充分的激勵，導致地磁觀測不充分，即觀測方程AX=b會遇到病態(tài)問題。本文以地磁導航磁力儀測量誤差補償為研究背景，將 TLS方法和Tikhonov正則化方法相結合，提出截斷總體最小二乘法(TTLS)[10,16]來解決地磁測量誤差補償?shù)牟B(tài)問題。在選擇正則化參數(shù)的方法上，考慮到L曲線法有時會由于曲線過于平滑而難以準確找到頂點，缺乏較好的準確性，因此采用廣義交叉檢核法（Generalized Cross-Validation, GCV）[11-12]來確定正則化參數(shù)。實驗結果證明，TTLS方法能有效抑制磁力儀標定中的病態(tài)問題，獲得了較好的磁力儀誤差補償效果。

1 磁力儀誤差特性建模

三軸捷聯(lián)磁力儀在使用過程中將會受到諸多誤差源的影響[13]，這些誤差源主要分為兩類：儀表誤差和載體干擾磁場。這兩類誤差源彼此耦合，共同影響磁力儀的測量精度。

1.1 磁力儀隨機誤差特征

當載體在某一固定位置或者磁場變化較小的地區(qū)作各種姿態(tài)的運動時，由于地磁場矢量為常矢量，捷聯(lián)式三軸磁傳感器的測量矢量滿足

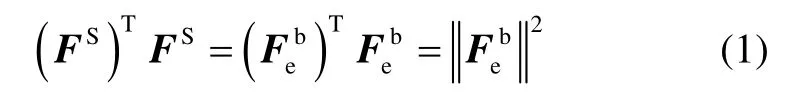
式中：F表示磁力儀的輸出，上標S表示傳感器坐標系， FS表示三軸磁力儀的輸出，代表當?shù)氐卮艌鲈谳d體坐標系的磁場矢量，上標b表示載體坐標系。將式(1)展開，寫成三分量形式：

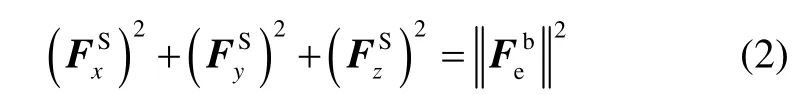
三軸間正交誤差是由于在制造過程中不能保證三個磁傳感器的測量軸完全兩兩正交而引起的測量誤差。非正交誤差模型如圖1所示。

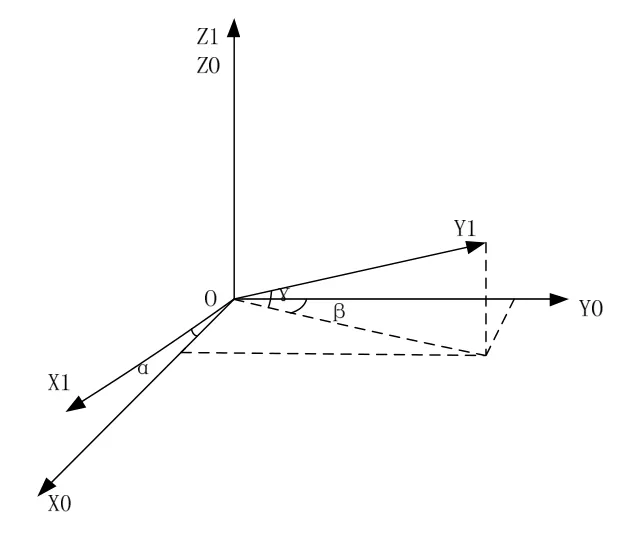
圖1 三軸磁傳感器的非正交模型Fig.1 Non-orthogonal model of three-axis magnetic sensor

圖1中，X0、Y0、Z0表示理想正交模型中三軸磁傳感器的矢量指向，X1、Y1、Z1表示實際磁傳感器三軸的指向。圖2中假設Z1軸與正交坐標系的Z0軸重合，且 X1O Z1面與 X0OZ0重合，X1軸在 X1O Z1面與軸X0的夾角為α、β為Y1在 X0OZ0面的投影與Y0的夾角，γ為Y1與 X0OZ0面的夾角。

據(jù)圖1所示的矢量關系，可以推導如下關系式：

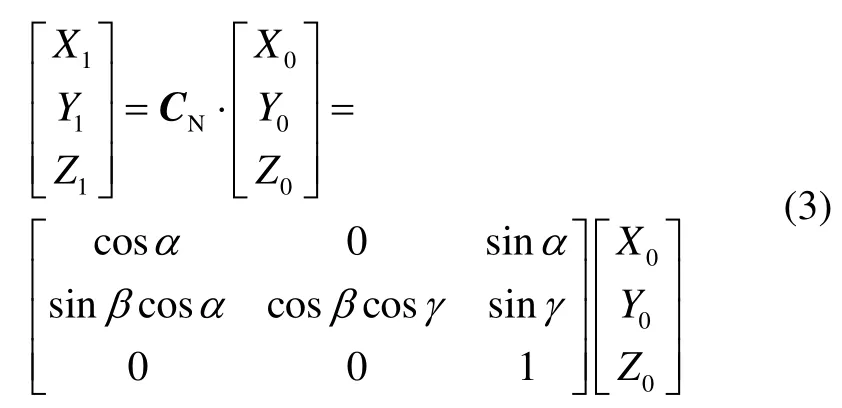
式(3)即為三軸磁傳感器的非正交數(shù)學模型。式中，CN是非正交誤差矩陣，X0、Y0、Z0為傳感器理論輸出值，X1、Y1、Z1為存在非正交誤差時的三維磁場強度。

傳感器的安裝會存在微小的方位誤差。設傳感器敏感軸與載體坐標軸的誤差角為 [εxεyεz]T，那么安裝誤差角數(shù)學模型為

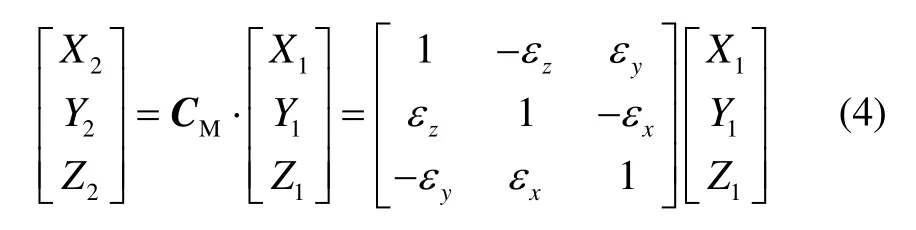
式中，CM表示安裝誤差矩陣，X2、Y2、Z2為存在安裝誤差時的三維磁場強度。

由于材料和制造工藝水平的限制，傳感器的三個軸之間的靈敏度、測量信號的放大電路特性不完全相同，導致存在三軸間存在刻度因子誤差，分別設為rx、ry、rz，那么刻度因子誤差數(shù)學模型為

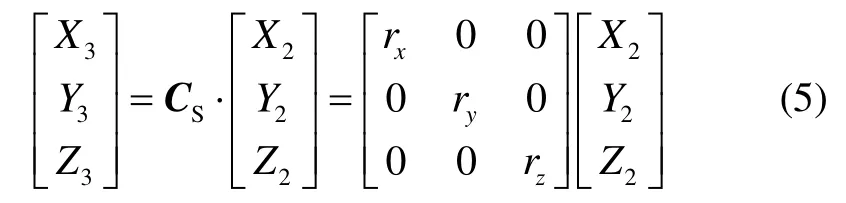
式中，CS表示刻度因子誤差矩陣，X3、Y3、Z3為存在刻度因子誤差時的三維磁場強度。

同時，由于剩磁現(xiàn)象，各敏感軸的激勵電路也存在零點漂移，使靜態(tài)工作點發(fā)生變化，并被逐級放大和傳輸，導致電路輸出端電壓偏離原固定值而上下漂動的現(xiàn)象。設傳感器三個方向的零點偏移分別為bx0、by0、bz0，那么零點漂移誤差數(shù)學模型為

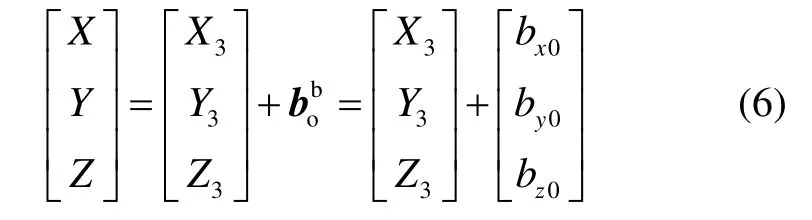
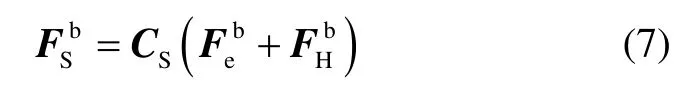
式中，CS稱為軟磁系數(shù)矩陣。

根據(jù)以上對磁力儀測量誤差特性的分析與建模，可以得到三軸磁力儀的測量輸出模型為

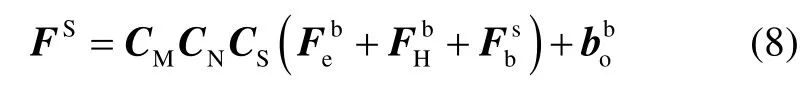
將式(3)～(7)代入到式(8)中，得到：

式中，對應系數(shù)矩陣和誤差矩陣分別為

其中：θ1～θ3是總非正交誤差角； k1～k3是總刻度因子誤差； o1～o3是總零偏誤差。因此，式(9)中的9參數(shù)能夠適當?shù)孛枋鋈S磁力儀的輸入輸出過程。

1.2 磁力儀的隨機誤差分析模型

式(9)進行逆向映射，可得到三軸磁力儀的標定模型為

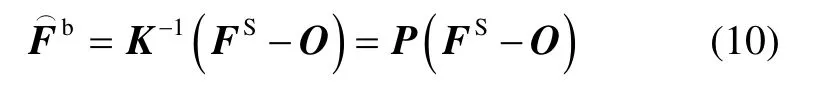
在一個磁場強度已知且恒定區(qū)域內，其場強標量值為定值，根據(jù)式(10)可得：

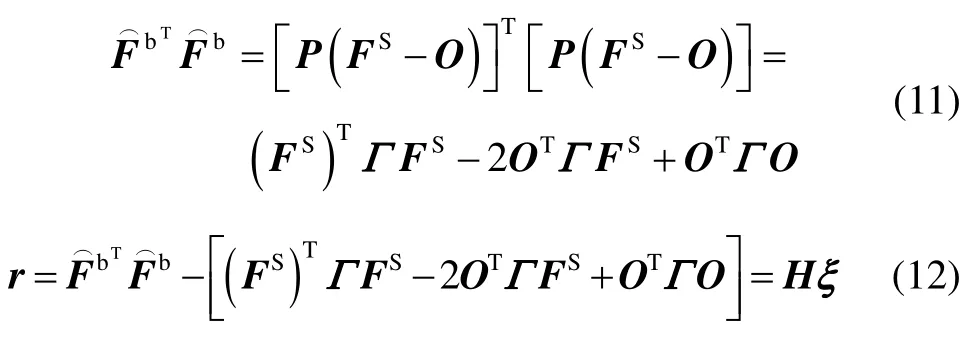
式中，

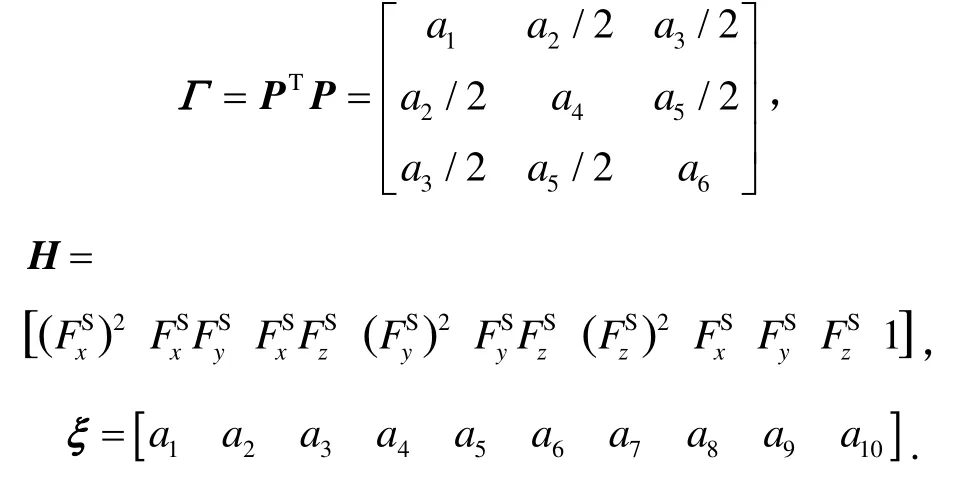
式(11)是一個橢球方程，式(12)為磁場強度真實值與測量值的平方差，當沒有隨機誤差干擾時，r= 0，r∈N×1，N為地磁測量數(shù)據(jù)個數(shù)。由于磁傳感器隨機誤差干擾的存在，只能通過估計橢球參數(shù)ξ，ξ∈10×1，得到 ，使殘差r最小，即有如下優(yōu)化指標：

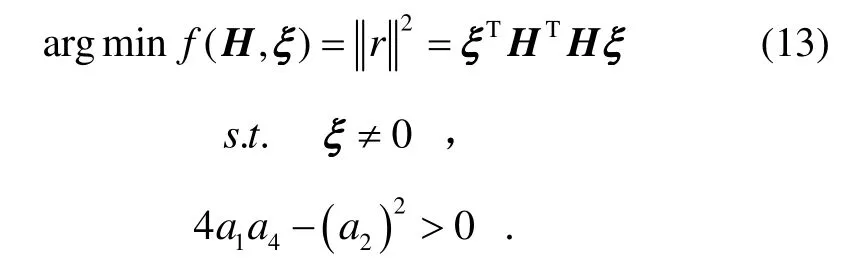
然后計算出 ρ1～ρ3、 k1～k3和o1～o3九個參數(shù)，完成誤差標定與補償?shù)倪^程。

2 隨機誤差補償算法

由式(12)可知，當r最小，也就是r=0的時候，式(13)優(yōu)化指標達到最優(yōu)。由于這是屬于非線性問題，需要進行線性化處理，將式(12)展開，得到如下線性方程：

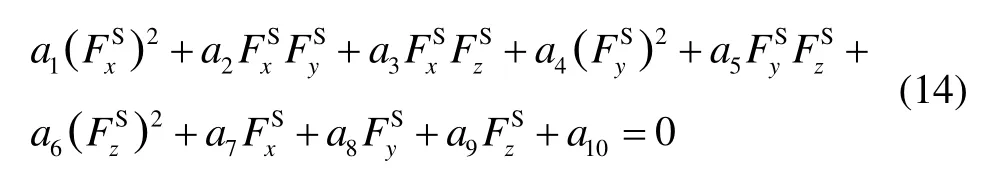
式中，

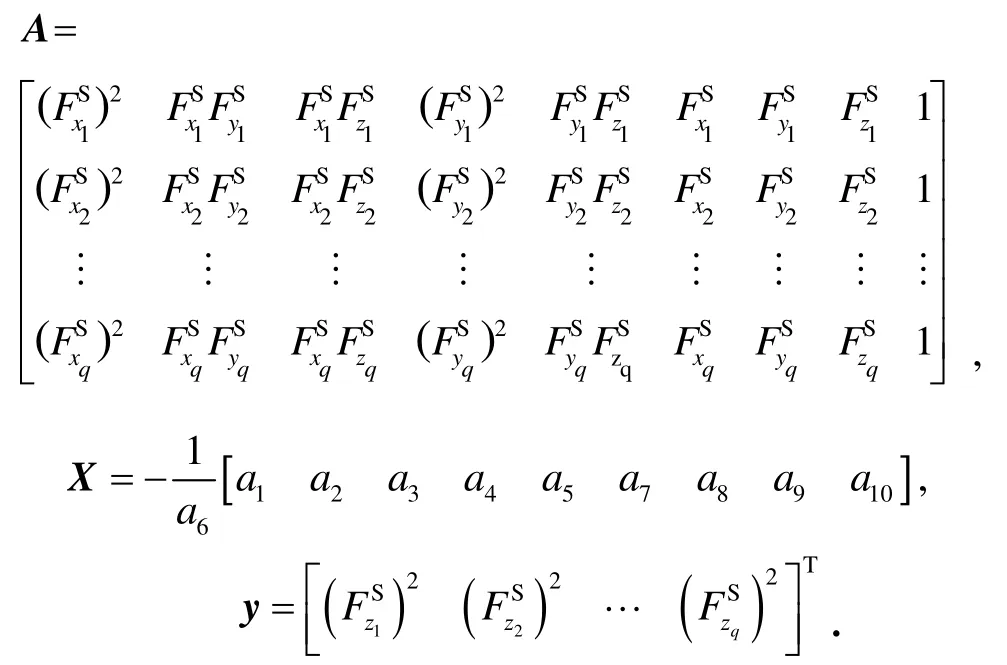
選擇q個測量值，對式(15)進行求解，由于q遠大于10，式(15)是超定的線性方程。在解得未知量X后，即可根據(jù)相關數(shù)學解算，求得誤差標定模型中的標定系數(shù)，方程解的精度將直接對誤差補償?shù)男Чa生影響。

如果系統(tǒng)矩陣A是精確的，而數(shù)據(jù)矢量b受到高斯白噪聲的影響，方程可以采用標準的最小二乘法進行估計，得到的估計值為

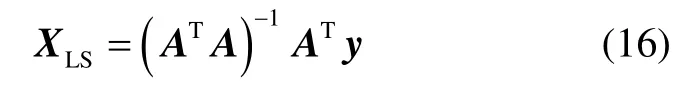
2.1 總體最小二乘法估計

式(16)的求解方法就是標準的最小二乘法(least square，LS)，是基于隨機誤差是高斯分布的假設[14]。但是，在磁力儀測量的觀測方程中，隨機誤差是非高斯分布的。另外，在磁力儀標定研究中，隨機誤差不僅分布在觀測矢量y中，還分布在系統(tǒng)矩陣A中，不滿足Gauss-Markov定理的條件。因此，在系數(shù)矩陣有較小的擾動時，最小二乘法的解可能有偏，甚至無解。

總體最小二乘(total least squares, TLS)需要得到的參數(shù)估值，需同時顧及系數(shù)矩陣A和觀測值y的隨機誤差，使得線性方程是相容的[15]。因此，TLS技術成為解決磁力儀參數(shù)標定與誤差補償?shù)姆椒ㄖ弧?/p>

在實際測量標定過程中，A和y會同時受到隨機誤差的干擾，不滿足最小二乘法的使用條件。這些隨機誤差是零均值獨立等方差σ分布的，將隨機誤差計入式(15)可得A和y的一階近似擾動為

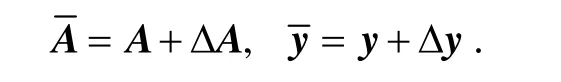
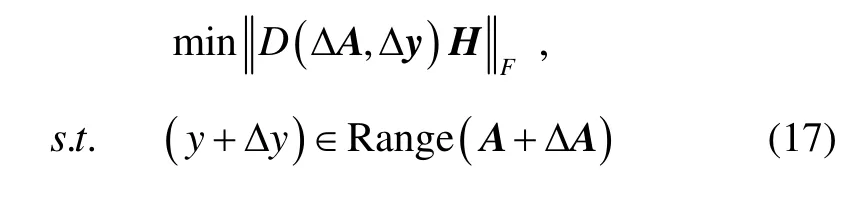
式中：非奇異對角矩陣 D=diag(d1,d2,…,dq)，di＞0；（ΔA,Δy）∈Rq×10；H=diag(h1,h2,…,h10)，hi＞0。因此找到干擾最小的約束最優(yōu)解即為 TLS解XTLS，對擴展矩陣 D(ΔA,Δb) H=U∑LT進行奇異值分解，其中U∈Rq×q，UTU=Iq，∑= diag （σ1,σ2,…,σ10）,且σ1≥ σ2≥ …≥ σ10， L ∈R10×10，LTL =I10，對應的右奇異值向量為 l1, l2,… ,l10。XTLS可以表示為

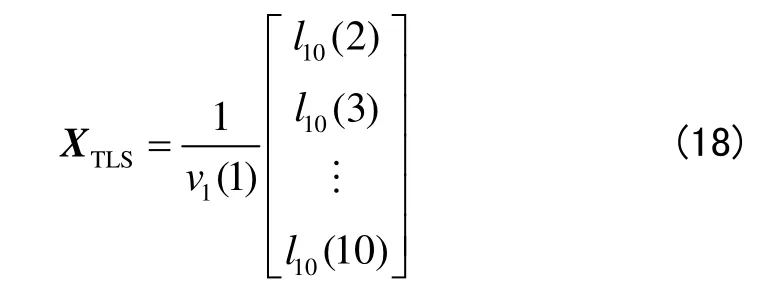
2.2 截斷總體最小二乘法

TTLS是在TLS的基礎上，利用廣義奇異值分解來解決觀測方程病態(tài)的問題[16]。TLS同時考慮了來自系數(shù)矩陣與觀測矩陣的擾動，要求這兩個擾動的Frobenius范數(shù)達到最小。然而，當觀測方程是病態(tài)的，TLS的解的范數(shù)會很大，使得求出的解毫無意義。TTLS適用于嚴重病態(tài)的、方程兩邊等式都存在誤差的線性問題。

對擴展矩陣 D （ΔA , Δb） H進行奇異值分解后，得到矩陣L。對矩陣L進行分塊：

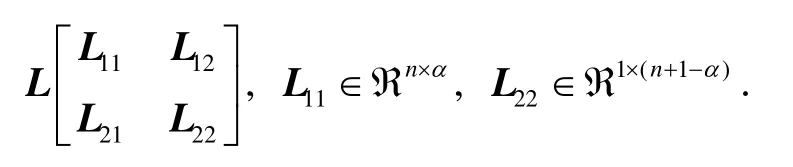
其中，n為觀測值數(shù)量，α(α≤n)為正則化因子。可得TTLS的解：

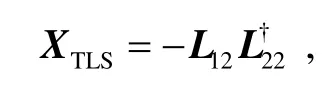
采用GCV(generalized cross-validation)法來求取正則化因子α。通過正則化能對病態(tài)問題的解估計增加合理的約束，保證解穩(wěn)定。對于Gauss-Markov約束項：

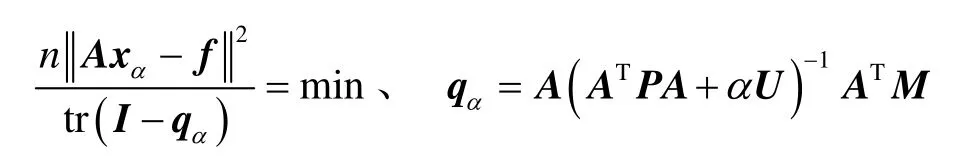
滿足 Axα= qαf，xα為待求參數(shù)，qα為影響矩陣，U為單位陣，為觀測值y誤差協(xié)方差矩陣，為單位權方差。

3 仿真驗證

在實測背景場中抽取 150個采樣點，對其進行TTLS隨機誤差分析，得到隨機誤差的估計值。本次仿真計算得正則化因子α=6，系數(shù)矩陣A的條件數(shù)為1.07×104，屬于嚴重病態(tài)問題。如圖2所示，曲線(1)是真實地磁場數(shù)據(jù)，曲線(2)是磁傳感器測量值，曲線(3)是經(jīng)過 TTLS補償后的數(shù)據(jù)。可以看出，經(jīng)過TTLS補償后的曲線與真實曲線基本重合，補償后殘差基本控制在10 nT以內，如圖3所示。

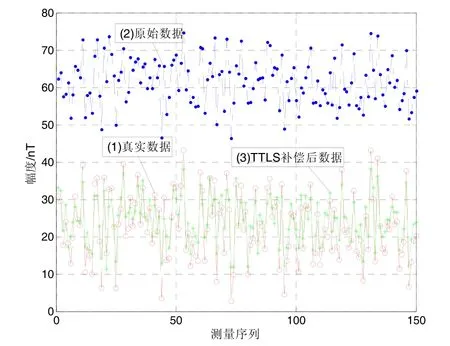
圖2 誤差補償效果對比圖Fig.2 Contrast on compensation results of random noise errors

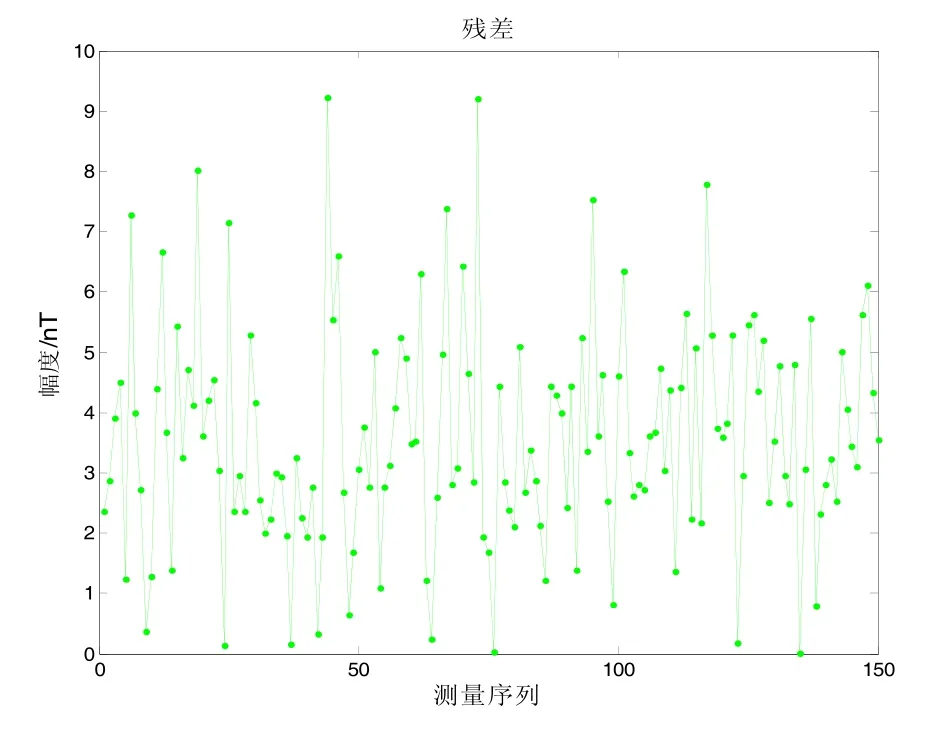
圖3 標定殘差Fig.3 Calibrated residual

為了驗證TTLS補償性能優(yōu)于TLS、LS的性能，用三種方法分別對同一地磁測量值進行誤差補償和殘差對比。下列選取一組實驗結果來說明，表1列出了三種標定方法估計磁力儀標定參數(shù)的結果。

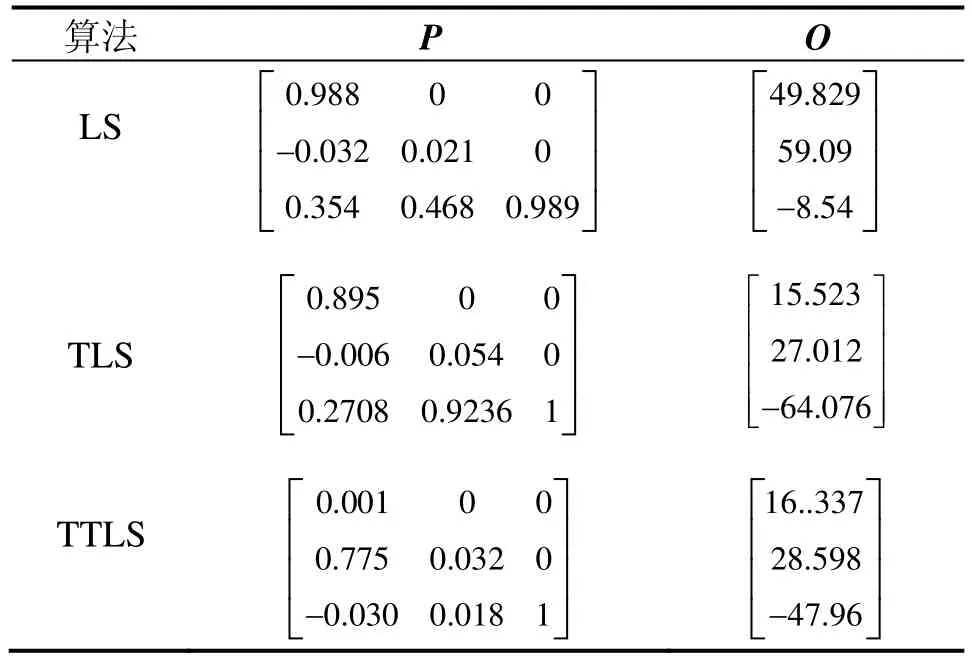
表1 三種方法的參數(shù)估計Tab.1 Parameters estimation of the three methods

圖4～5依次是三種標定方法分別在X、Y、Z方向的對比圖，曲線(1)是真實地磁場數(shù)據(jù)，曲線(2)～(4)分別是LS、TLS、TTLS標定后的數(shù)據(jù)。可以看出，經(jīng)過 LS補償后的數(shù)據(jù)離真實值比較遠，這是由于系數(shù)矩陣A的病態(tài)性導致LS解算結果誤差較大。同樣看出，三種標定方法的性能由強到弱依次是TTLS、TLS、LS。圖6～7依次是三種標定方法分別在X、Y方向的殘差對比圖，同樣可以看出TTLS的補償性能優(yōu)于其它兩種方法，達到了誤差補償?shù)男Ч?/p>

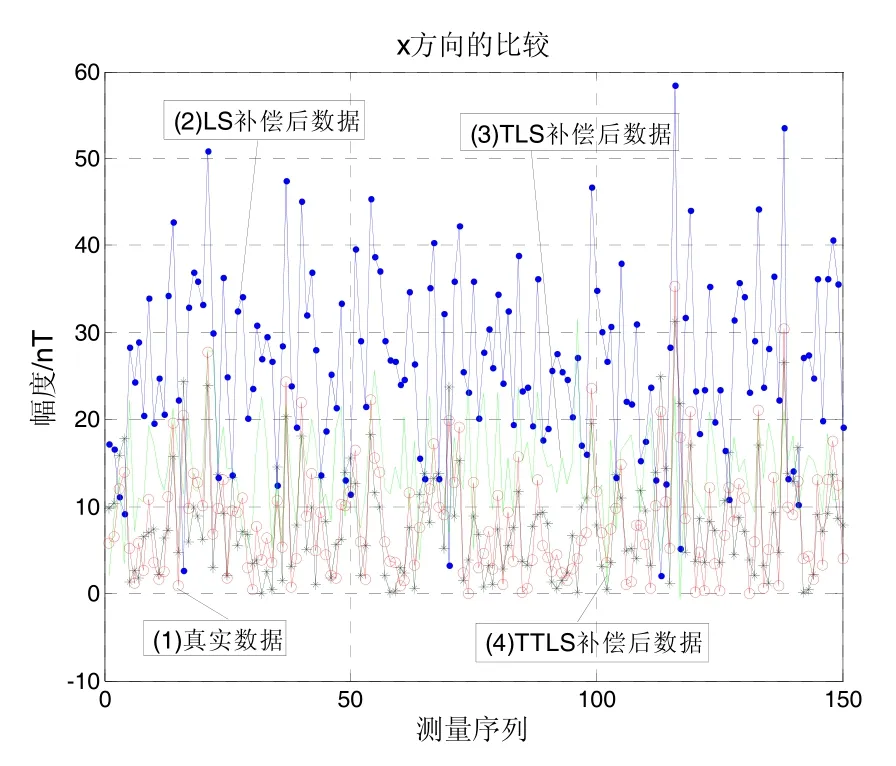
圖4 x方向補償對比圖Fig.4 Contrast on compensation results of

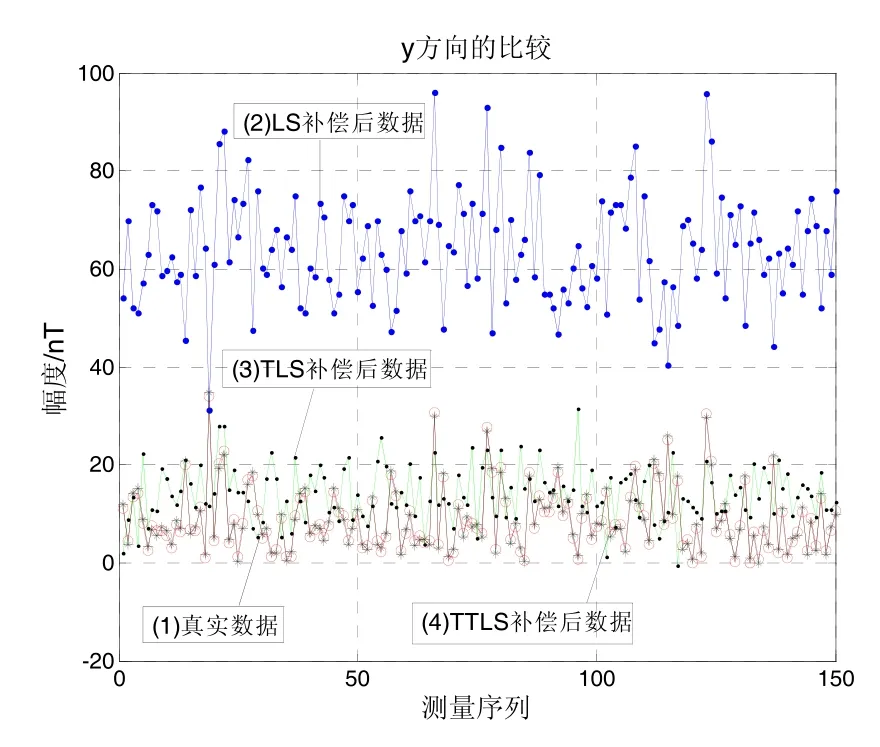
圖5 y方向補償對比圖Fig.5 Contrast on compensation results of

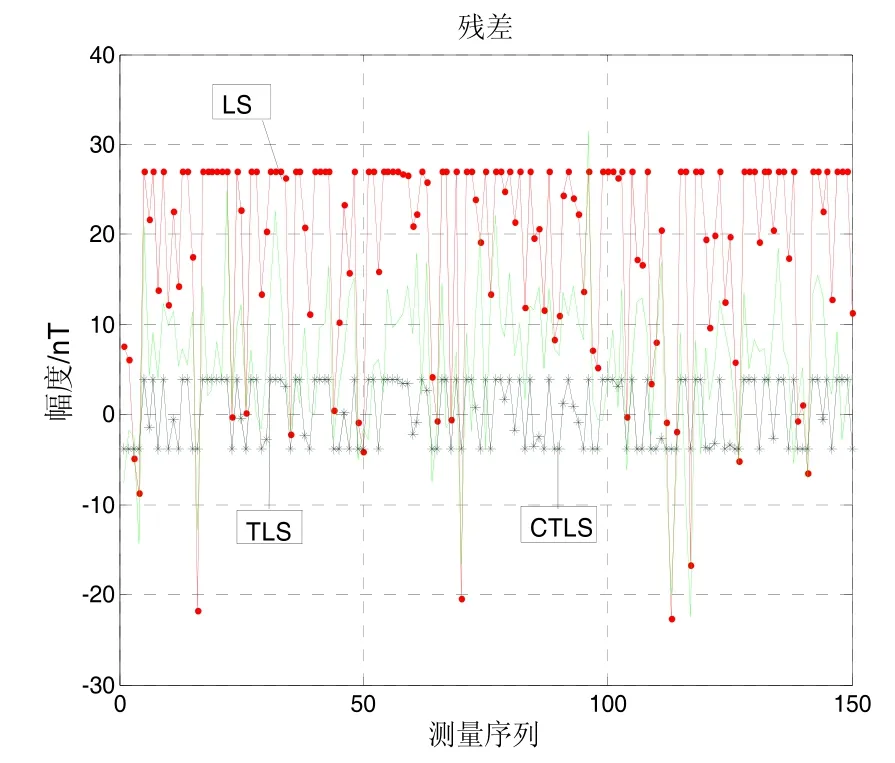
圖6 x方向殘差對比圖Fig.6 Contrast on residuals of direction

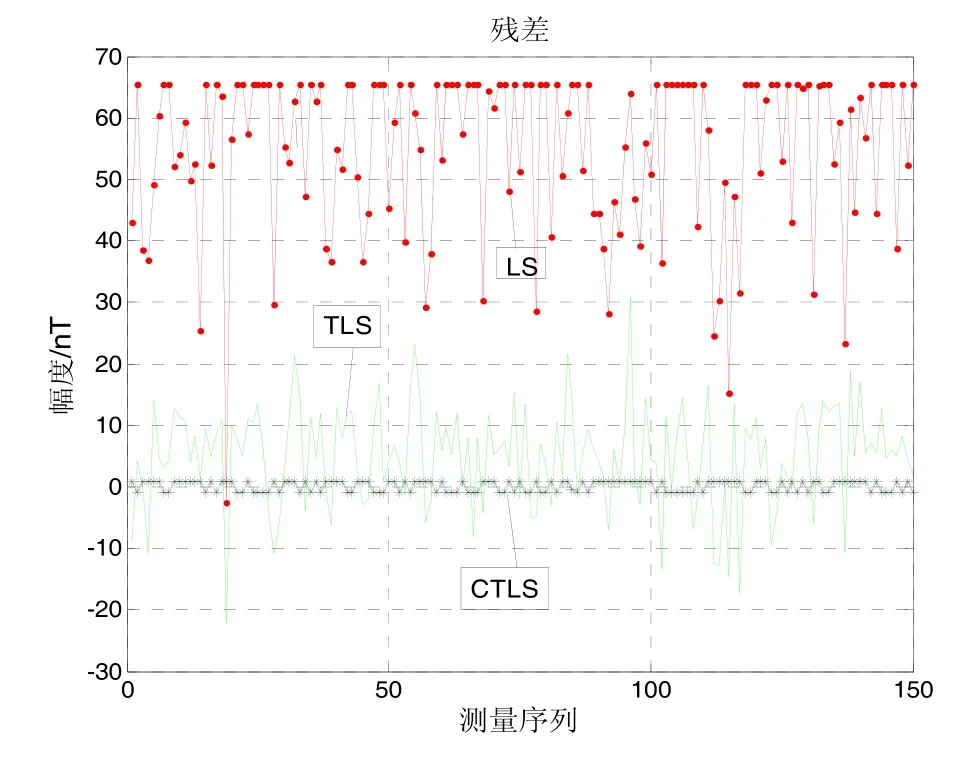
圖7 y方向殘差對比圖Fig.7 Contrast on residuals of direction

4 結 論

水下地磁導航的磁力儀的測量環(huán)境復雜，受到多種誤差因素和觀測數(shù)據(jù)不足的影響。依據(jù)誤差特性建立誤差分析模型后，需利用合理的方法對模型進行修正。TLS適用于觀測方程兩端存在的誤差的情況，卻無法解決海洋磁測數(shù)據(jù)不充分引起的病態(tài)問題。TTLS是TLS的自然擴展，它既適用于方程兩端存在誤差的情況，也適用于處理磁力儀測量的病態(tài)問題。仿真結果表明，TTLS法誤差補償性能優(yōu)于LS法和TLS法，將未補償前的地磁測量殘差從150 nT減小到10 nT以內。說明TTLS方法能夠解決磁力儀測量病態(tài)問題，提高了參數(shù)估計的精度，達到了抑制隨機誤差的目的。

（References）：

[1] 江勝華, 申宇, 褚玉程. 基于磁偶極子的磁場梯度張量縮并的試驗驗證及相關參數(shù)確定[J]. 中國慣性技術學報, 2015, 23(1): 103-114. Jiang Sheng-hua, Shen Yu, Chu Yu-cheng. Experimental verification and related parameter’s determination for magnetic gradient tensor contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 103-114.

[2] 朱占龍, 單友東, 楊翼, 等. 基于新息正交性自適應濾波的慣性/地磁組合導航方法[J]. 中國慣性技術學報, 2015, 23(1): 66-70. Zhu Zhan-long, Shan You-dong, Yang Yi, et al. INS/GNS integrated method based on innovation orthogonality adaptive Kalman filter[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 66-70.

[3] 管志寧. 地磁場與磁力勘探[M]. 北京: 地質出版社, 2005: 90-98. Guan Zhi-ning. Geomagnetic field and magnetic exploration[M]. Geological Publishing House, 2005: 90-98.

[4] Siddharth S, Ali A S, El-Sheimy N, et al. A gametheoretic approach for calibration of low-cost magnetometer under uncertainty[J]. Measurement Science and Technology, 2012, 23(2): 344-347.

[5] Foster C C, Elkaim G H. Extension of a non-linear, two-step calibration methodology to include non-orthogonal sensor axes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1070-1087.

[6] Gebre-Egziabher Demoz, Elkaim G H, Powell J D, et al. Calibration of strapdown magnetometers in magnetic field domain[J]. Journal of Aerospace Engineering, 2006: 87-102.

[7] Valerie R, Muhammad H A, Gerard L. Complete triaxis magnetometer calibration in the magnetic domain[J]. Journal of Sensors, 2010: 1-9.

[8] Rhode S, Usevich K, Markovsky I, Gauterin F. A recursive restricted total least-squares algorithm[J]. IEEE Transactions on Signal Processing, 2014, 62(21): 5652 - 5662.

[9] 吳志添, 武元新, 胡小平, 等. 基于總體最小二乘的捷聯(lián)三軸磁力儀標定與地磁場測量誤差補償[J]. 兵工學報, 2012, 33(10): 1202-1209. Wu Zhi-tian, Wu Yuan-xin, Hu Xiao-ping, et al. Calibration of strapdown three-axis magnetometer and measurement error compensation of geomagnetic field based on total least squares[J]. Acta Armamentarii, 2012, 33(10): 1202-1209.

[10] Sima D M, van Huffel S. Level choice in truncated total least squares[J]. Comput Stat Data Anal, 2007, 52(2): 1103-1118

[11] Golub G H, Heath M, Wahba G. Generalized crossvalidation as a method for choosing a good ridge parameter[J]. Technometrics, 2012, 21(2): 215-223.

[12] Feng Tian-shu, Zhuang Fu-zhen, He Qing. Improving ESVM with generalized cross-validation[C]//2015 International Joint Conference on Neural Networks. 2015: 1-8.

[13] Kiani M, Pourtakdoust, Sheikhy S H, Akbar A. Consistent calibration of magnetometers for nonlinear attitude determination[J]. Measurement, 2015, 73: 180-190.

[14] Cai Bin-lei, Guo Qin. Spectral methods for least square regression learning[J]. ICIC Express Letters, 2015, 9(6): 1577-1582.

[15] Lipor J, Balzano L. Robust blind calibration via total least squares[C]//2014 IEEE International Conference on Acoustics, Speech and Signal Processing. 2014: 4244-4248.

[16] Fierro R D, Golub G H, Hansen P C, et al. Regularization by truncated total least squares[J]. SIAM J. SCI. Comput., 1997, 18(4): 1223-1241.

Truncated total least squares algorithm in restraining random error of geomagnetic navigation magnetometer

WANG Li-hui1, YU Le1, LIANG Bing-bing2, QIAO Nan1
(1. Key Laboratory of micro-inertial instrument and advanced navigation technology, Ministry of education, School of instrument science and engineering, Southeast University, Nanjing 210096, China; 2. Science and Technology on Space Physics Laboratory, Beijing 100076, China)

Three-axis magnetometer measurement random error compensation is currently a hot topic in underwater geomagnetic navigation research field. Traditional methods are based on least squares (LS), total least squares (TLS) or other improved methods to compensate measurement random errors, supposing that measurement random errors are Gaussian or without ill-posed problems of magnetometer observation equation. To solve the ill-posed problems and/or to reduce the measurement random error existed in both sides of observation equation, a method named truncated total least squares (TTLS) is proposed. The TTLS combines (TLS) with regularization method. Simulation results demonstrate that the TTLS can effectively inhibit the pathological influence of the magnetometer measurement, and the residual between the real data and the data after TTLS calibration can be decreased to 10 nT. Moreover, comparing with the measurement data after TLS compensation and LS compensation, the data after TTLS compensation are closer to the real data, achieving the purpose of restraining the measurement random errors.

underwater geomagnetic navigation; three-axis magnetometer; ill-posed problem; truncated total least squares; random error compensation

U666.1

：A

2015-09-21；

：2015-11-25

國家自然科學基金資助項目（61203192，51477028）；船舶工業(yè)預研基金（13J3.8.4）；中央高校基本科研業(yè)務費專項資金資助（東南大學優(yōu)秀青年教師項目-2242013R30016）

王立輝（1979—），男，博士生導師，副教授，從事導航、精密儀器等方面的應用研究。E-mail: wlhseu@163.com

1005-6734(2015)06-0763-06

10.13695/j.cnki.12-1222/o3.2015.06.012