加速度計全量程標度因數不對稱性標定算法研究

王 洋，于湘濤，吳 楠，魏 超，張 吉

（北京自動化控制設備研究所，北京 100074）

0 引言

加速度計是慣性導航系統的核心器件之一，廣泛應用于航空、航天、船舶以及兵器系統的導航制導與控制中[1]。標度因數不對稱性作為慣導系統速度誤差的影響因素之一，其標定精度的提高對慣導系統導航精度的提升具有重要意義。

標度因數不對稱性是對加速度計在正向、負向輸入加速度條件下標度因數差異性的一種度量[2]。目前加速度計標度因數不對稱性研究多見于重力場環境，隨著加速度計指標精度的提高和輸入量程的增大，需要對全量程范圍內的標度因數不對稱性進行研究[3-4]。

目前加速度計全量程高階非線性系數大多通過精密離心機試驗進行標定，而試驗過程中由離心加載引起的各種誤差，對其標度因數和偏值等線性指標的標定精度影響較大。如何辨識加速度計精密離心機測試過程典型誤差，并進行誤差控制，是進行全量程標度因數不對稱性標定的關鍵。

1 加速度計精密離心機測試誤差分析與數據處理方法

精密離心機測試是對加速度計高過載特性進行測試的常用方法，利用離心機產生的高g值的持續向心加速度作為加速度計的輸入，用于測量與標定加速度計與高過載有關的各種誤差系數[5]。

1.1 加速度計精密離心機測試誤差分析

在加速度計精密離心機測試過程中，由于測試設備與測試方法的局限，會產生各種誤差。文獻[6]將其歸納為半徑不確定性、對準不確定性、角速度誤差、加速度計溫度影響、試驗過程中的趨勢項，以及加速度計信號測量誤差等方面。各類誤差與加速度計輸出系數的對應關系如圖1所示。

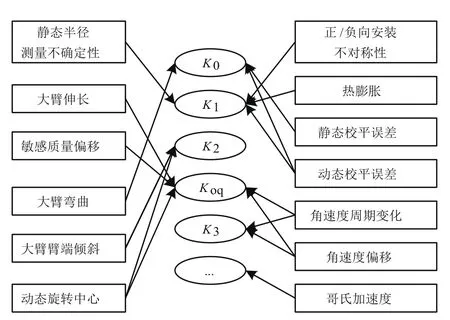
圖1 加速度計精密離心機測試典型誤差Fig.1 The typical errors in accelerometer precision centrifuge testing

精密離心機測試的主要問題是半徑不確定性與對準不確定性。其中半徑不確定性影響因素包括靜態半徑的不確定性、半徑的動態變化和由于環境導致的半徑變化[6-11]。

1）靜態半徑不確定性

為確定待測加速度計有效質量中心的靜態半徑，需要明確大臂的中心位置、有效質量中心相對于加速度計基準面的位置以及這些位置之間所有機械構件的尺寸和相互關系。大部分離心機不能提供直接測量靜態半徑的手段，在實際過程中靜態半徑一般通過待測加速度計的輸出來估算。

式中：R0為離心機靜態半徑，Er為離心機旋轉時的輸出平均值，Es為離心機靜止時的輸出平均值，K1為當前環境下的標度因數值。

2）離心機大臂伸長

大臂伸長是指連接加速度計和離心機旋轉軸的機械結構超出靜態值R0的伸長，由離心加載引起。僅考慮大臂伸長影響，實際的半徑方程為：

式中：R為實際轉臂長度，R0為離心機轉臂靜態值，CAS為常數，與轉臂材料等相關，量綱為加速度的倒數，a0為標稱向心加速度。

3）加速度計檢測質量偏移

在離心加載作用下，檢測質量偏移導致加速度計有效質量中心半徑的變化，其影響機理與大臂伸長相似，均正比于施加的向心加速度。

4）加速度計正負向安裝不對稱性

加速度計有效質量中心的位置在微小范圍內不可測定，當待測加速度計輸入軸倒置時，徑向位置會產生誤差，會導致輸出數據的標度因數不對稱性，從而惡化線性度系數的評估。此外，徑向不對稱性還會嚴重影響偶次項系數。

在精密離心機測試過程中，由于離心加載作用，無論加速度計正向或負向安裝，大臂伸長、敏感質量偏移等都會加大輸入加速度的數值，即輸入加速度正向時表現為正，負向時表現為負，即奇異二次項系數。在精密離心機標定時，必須對奇異二次項系數加以考慮，否則會對其它系數標定精度產生影響。

1.2 加速度計精密離心機測試數據處理方法

加速度計模型方程是表述加速度計輸出E與沿加速度計基準軸作用的加速度之間關系的表達式，完整的加速度計輸出模型方程如式（4）所示。

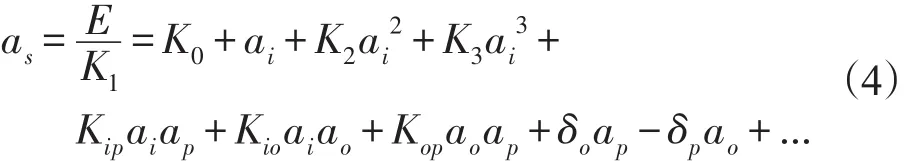
式中：E為加速度計輸出，ai、ao、ap分別為沿輸入軸、輸出軸和擺軸的加速度，K0為偏值，K1為標度因數，K2、K3為高次項系數，Koq為奇異二次項系數，Kip、Kio、Kpo為交叉耦合系數，δo、δp為安裝誤差角。

在測試過程中，受靜態半徑不確定性、離心機大臂伸長、敏感質量偏移和安裝誤差等因素影響，真實的加速度計輸出模型如式（5）所示。

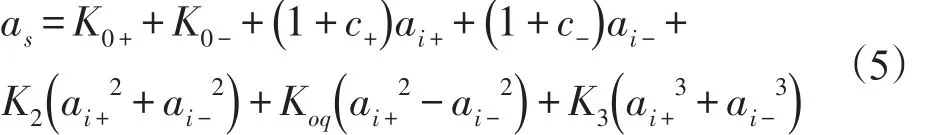
為便于運算，將式（5）重新排列如式（6）。

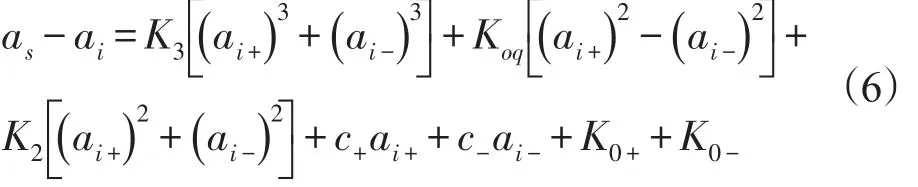
其中，帶有下標+的項僅當ai＞0時適用，帶有下標–的項僅當ai＜0時適用，as為加速度計輸出值，ai為沿輸入軸IA的加速度，c-ai-、c+ai+為由于半徑測量和安裝誤差引起的估算輸入加速度誤差的一次近似值。

為充分利用試驗數據，盡可能的減小誤差，構造與求解參數相關的測試數據矩陣A，求解系數矩陣K以及輸出矩陣B，三者之間關系如式（7）所示[6]。

對于式（7），根據最小二乘算法，存在正規方程ATAK=ATB，應用矩陣逆變法，得到系數矩陣如式（8）。

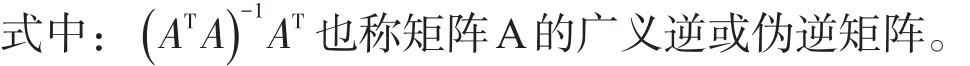
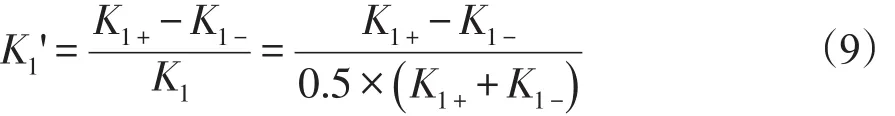
式中：K1'為標度因數不對稱性，K1+為正向標度因數，K1-為負向標度因數。

在精密離心機測試中，由于離心加載引起的各種誤差，對線性項標度因數K1、偏值K0的標定精度影響較大，進而影響到全量程標度因數不對稱性的標定。為改善精密離心機測試對加速度計線性指標的標定，在典型誤差分析的基礎上，給出利用精密離心機試驗進行加速度計全量程標度因數不對稱性標定的原則：以標度因數誤差c-、c+作為測試過程精度指標，對輸入數據進行迭代，直至c-、c+降低到10-8水平。對修正后的數據進行三階擬合，得到加速度計全量程標度因數不對稱性。

加速度計全量程標度因數不對稱性標定流程如圖2所示。

2 加速度計全量程標度因數不對稱性標定算法

加速度計標度因數不對稱性是對正向、負向加速度輸入條件下，標度因數差異性的一種度量。在實際應用中，一般用正向與負向輸入加速度測定值的差值與其平均值的比值進行衡量，即：

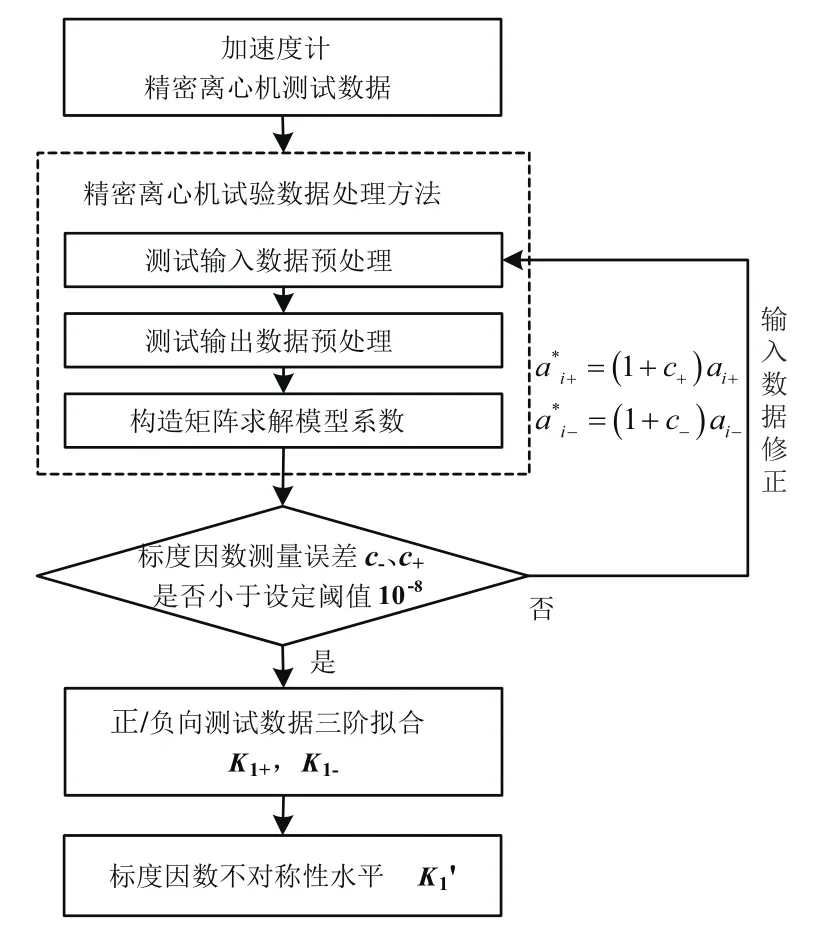
圖2 加速度計全量程標度因數不對稱性標定流程Fig.2 The calibration steps for accelerometer full-range scale factor asymmetry

3 試驗驗證

為驗證文中提出的標定算法，抽取10只加速度計進行精密離心機試驗。試驗結束后，按照上述算法計算出測試數據修正前后的標度因數誤差c-、c+，如表1所示。

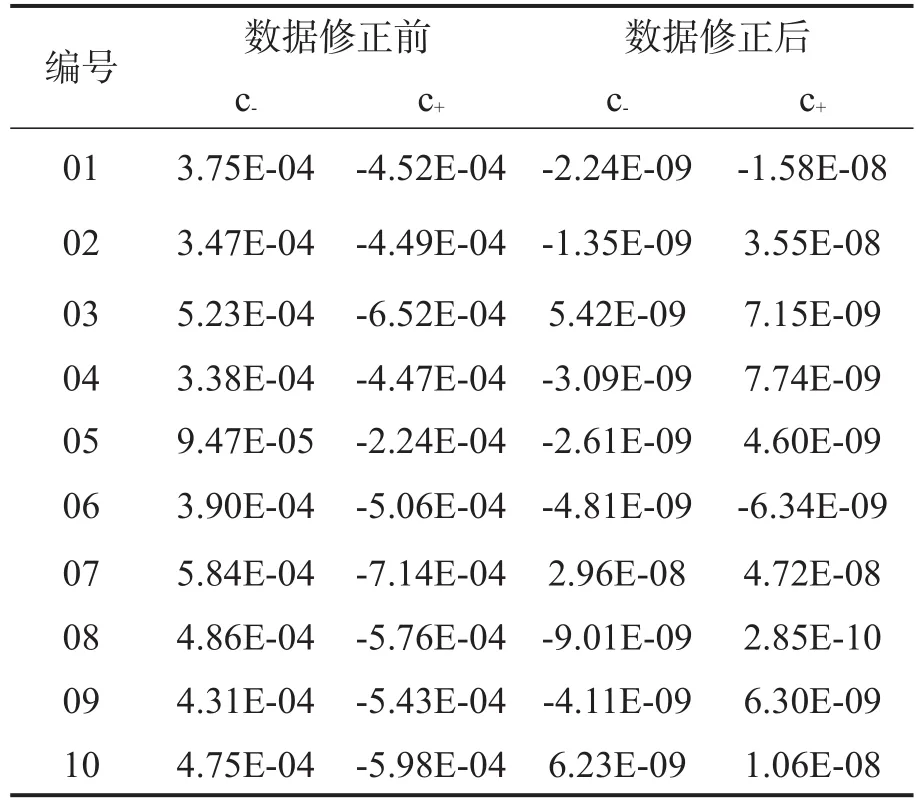
表1 標度因數誤差c-、c+修正前后對比Tab.1 Acomparison of scale factor errors between the original and revised testing datas

從表1可以看出，通過輸入數據修正，標度因數測試誤差c+、c-快速收斂，從10-4降低至10-9，證明了通過測試數據修正，能夠有效降低離心機測試誤差對加速度計線性系數標定精度的影響。

對修正后的測試數據，應用式（10）進行三階多項式擬合求取標度因數，并與重力場下標度因數標定值進行對比，如表2所示。

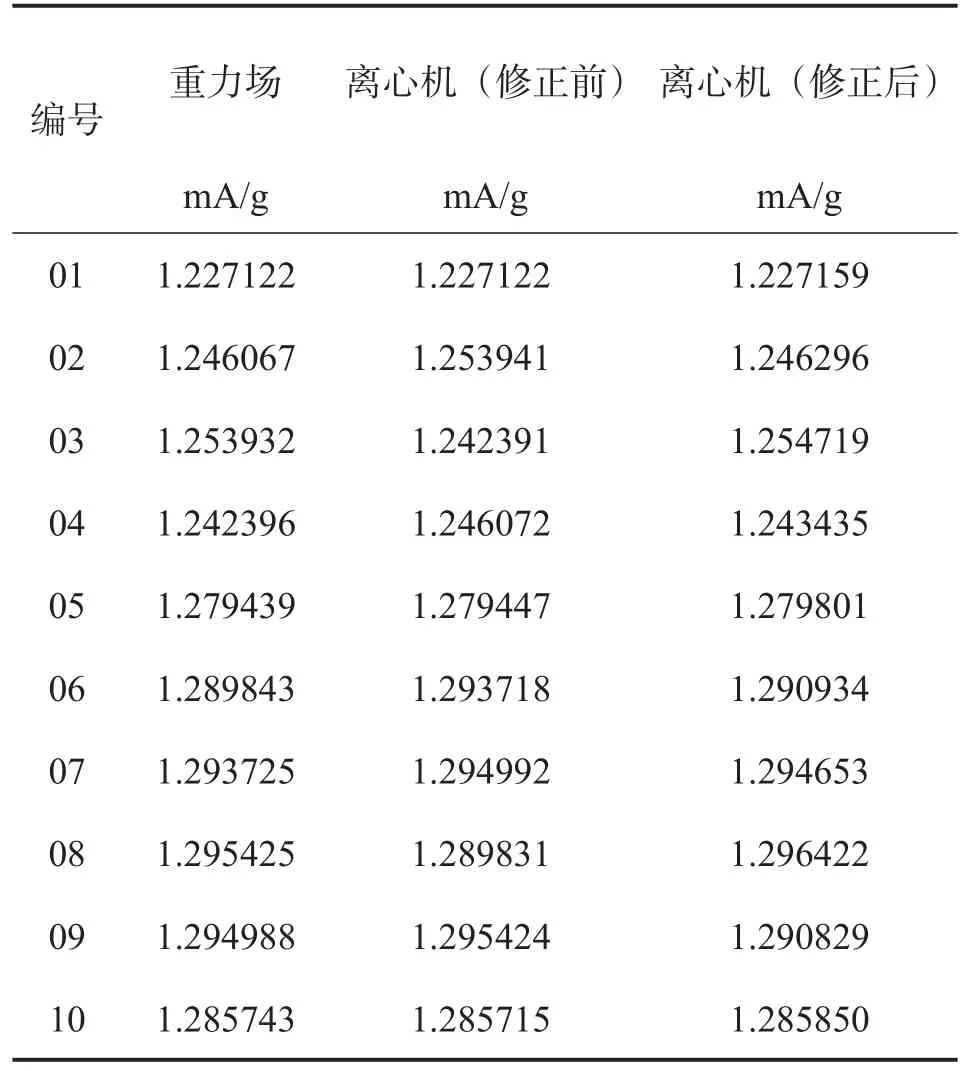
表2 重力場與離心機標度因數標定值對比Tab.2 Acomparison of scale factors in gravity field and precision centrifuge testing

從表2可以看出，加速度計精密離心機測試數據修正后，應用三階擬合得到的標度因數標定值與重力場標定值非常接近（相差10-4水平），證明了通過數據修正能夠得到較高精度的標定因數標定值，也為全量程標度因數不對稱性標定奠定了基礎。

對修正后的測試數據，計算正向標度因數K1+、負向標度因數K1-，并應用式（9）得到全量程范圍內標度因數不對稱性水平K1'，如表3所示。

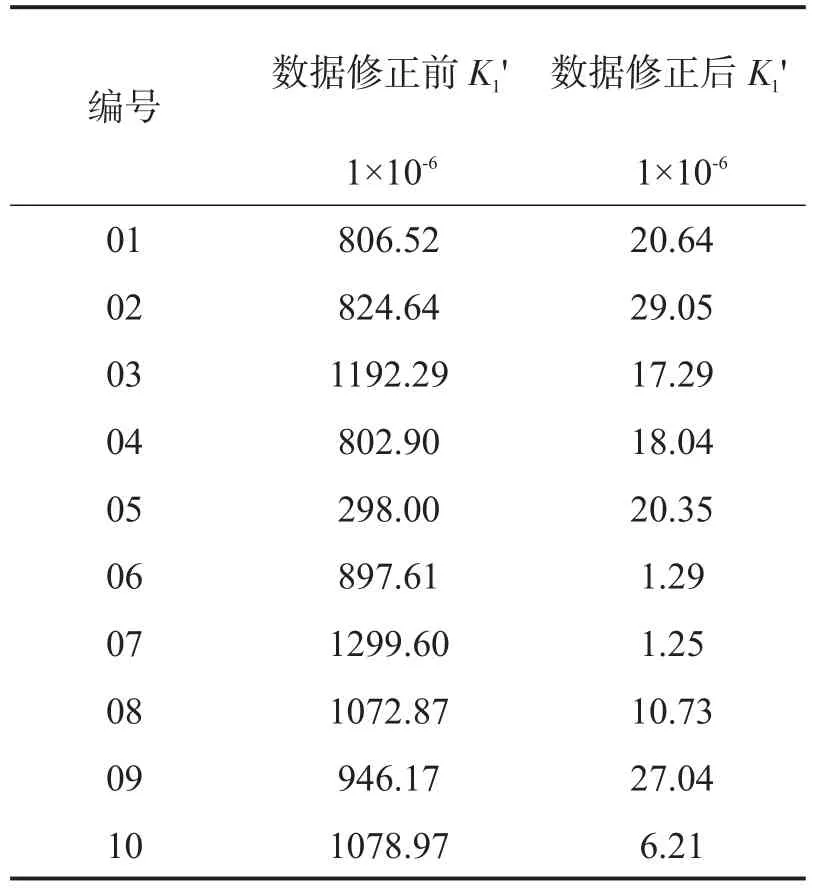
表3 加速度計全量程標度因數不對稱性K1'標定結果Tab.3 Acomparison of full-range scale factor asymmetry between the original and revised testing data

從表3可以看出，利用文中提出的算法對加速度計測試數據進行修正后，可以將標度因數不對稱性K1'從10-4提高至10-5，提高了加速度計全量程標度因數不對稱性的標定精度。

4 結論

重力場四點翻滾法是加速度計標度因數K1和偏值K0標定的常用方法，但由于僅能提供-1g～1g輸入加速度，無法給出全量程標度因數不對稱性K1'的有效信息。而精密離心機測試由于測試過程引入的各種誤差，不能直接實現對加速度計標度因數的精確標定。

在加速度計精密離心機測試誤差分析的基礎上，提出了一種加速度計全量程標度因數不對稱性標定算法，并對其進行了驗證。驗證結果表明，文中提出的算法能夠將標度因數測試誤差c-、c+從10-4降低至10-9，標度因數不對稱性K1'的標定精度從10-4提高至10-5。

[1]吳亮華，鄭辛，李群，等.高精度激光捷聯慣導行進中方位對準技術[J].戰術導彈技術，2008（1）:73-78.

[2]GJB 1037A-2004.單軸擺式伺服線加速度計試驗方法[S].

[3]趙連元.石英撓性加速度計目前測試方法的局限性分析[J].戰術導彈控制技術，2005,49（2）:72-77.

[4]蔣效雄，劉雨，蘇寶庫.高精度加速度計重力場標定試驗方法[J].吉林大學學報（工學版），2010.4（1）:287-291.

[5]JJF 1116-2004.線加速度計的精密離心機校準規范[S].

[6]Std 836TM-2001.IEEE recommended practice for precision centrifuge testing of linear accelerometers[S]．The Institute of Electrical and Electronics Engineers．

[7]安金剛,王珺,張蘭.石英撓性加速度計精密離心測試的非線性系數重復性探討[J].戰術導彈控制技術，2006,53（2）:80-82.

[8]邢海峰,任順清,祁家毅,等.加速度計二次奇異項系數的形成機理與標定方法[J].航天控制,2009,27（2）:91-95.

[9]喬仁曉,孟曉風,季宏.加速度計非線性項系數校準誤差分析與建模[J].系統仿真學報,2008,20（6）:1633-1635.

[10]徐永,賀忠江,喬仁曉,等.線加速度計高次項系數校準初探[J].計測技術,2008,28（5）:14-19.

[11]王世明,任順清.精密離心機誤差對石英撓性加速度計誤差標定精度分析[J].宇航控制，V33（4）:520-526.