創(chuàng)建更具理性色彩的數(shù)學(xué)課堂

葉玲

[摘 要]學(xué)生的數(shù)學(xué)理性能力是在數(shù)學(xué)學(xué)習(xí)過程中自然孕育和生成的。毫無疑問，數(shù)學(xué)課應(yīng)該充分體現(xiàn)、表達(dá)數(shù)學(xué)的特點(diǎn)，并讓學(xué)生在數(shù)學(xué)的光芒照耀下，形成與之適應(yīng)的學(xué)習(xí)風(fēng)格、思維特點(diǎn)。通過具體的教學(xué)案例分析，為創(chuàng)建更具理性色彩的數(shù)學(xué)課堂提供一些思考。

[關(guān)鍵詞]理性色彩 數(shù)學(xué) 認(rèn)識分?jǐn)?shù)

[中圖分類號] G623.5 [文獻(xiàn)標(biāo)識碼] A [文章編號] 1007-9068（2015）08-005

“分?jǐn)?shù)的初步認(rèn)識”是一節(jié)經(jīng)典課，曾在各種層次的教研活動中大放異彩，被吳正憲、黃愛華、朱樂平、張齊華、周衛(wèi)東、許衛(wèi)兵等多位名師演繹過，他們有的注重情境，有的著力探索，有的凸顯文化，有的關(guān)注基礎(chǔ)，有的扣住理解，有的強(qiáng)化應(yīng)用，可謂是亮點(diǎn)紛呈，各具特色。不過，數(shù)學(xué)是自然科學(xué)的基礎(chǔ)學(xué)科，理性精神是其核心精神。數(shù)學(xué)思維的訓(xùn)練、數(shù)學(xué)方法的感悟、數(shù)學(xué)活動經(jīng)驗(yàn)的積累，都離不開數(shù)學(xué)理性的參與。透過名師的課堂，可以感受到充滿理性色彩的課堂魅力。本文以許衛(wèi)兵老師“分?jǐn)?shù)的初步認(rèn)識”一課為例，談?wù)剛€(gè)人的感想。

一、高點(diǎn)定位，整體“布局”，首尾呼應(yīng)

從什么樣的角度來引入分?jǐn)?shù)，是分?jǐn)?shù)的初步認(rèn)識的首要命題。回顧以往的教學(xué)，通常有兩種方式：一種以朱樂平老師為例，從“1÷2”中分?jǐn)?shù)與除法的關(guān)系入手;一種以吳正憲老師和張齊華老師為例，從將多個(gè)物體平均分兩份過渡到將一個(gè)物體平均分兩份，讓學(xué)生憑著日常生活經(jīng)驗(yàn)體會“平均分”與“一半”的豐富含義，為接下來學(xué)習(xí)分?jǐn)?shù)打開思路。這兩種方式其實(shí)有相通之處，算式“1÷2”同樣可以理解為一個(gè)物體平均分成兩份，本質(zhì)是一樣的。許衛(wèi)兵老師的站位似乎上了一個(gè)臺階，從“數(shù)系”的角度出發(fā)，引領(lǐng)學(xué)生在整數(shù)之外，尋找分?jǐn)?shù)的蹤跡，并最終實(shí)現(xiàn)二者的統(tǒng)一。

課始，師生從“數(shù)”的讀音聊起，引出數(shù)學(xué)家華羅庚的話“數(shù)（shù）起源于數(shù)（shǔ）”，然后數(shù)蘋果的個(gè)數(shù)，得出1、2、4等數(shù)，并告知在數(shù)學(xué)上這樣的數(shù)叫“整數(shù)”。

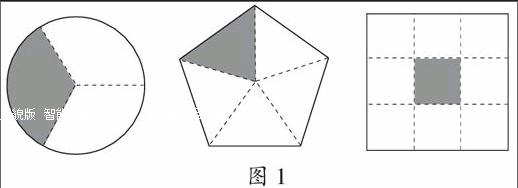
課尾，讓學(xué)生看圖寫分?jǐn)?shù)（如圖1）。隨著一個(gè)圖形被平均分的份數(shù)增加后，學(xué)生開始出現(xiàn)了“點(diǎn)數(shù)（shǔ）”的情況。

師（一邊做點(diǎn)數(shù)的動作，一邊追問學(xué)生）：你們這是在干什么呢？

生：我們在數(shù)呢！

師：數(shù)什么呢？

生：數(shù)平均分成了幾份，還數(shù)涂色的部分。

師：華羅庚爺爺說“數(shù)起源于數(shù)”，看來，不僅整數(shù)和數(shù)（shǔ）有關(guān)系，分?jǐn)?shù)和數(shù)（shǔ）也——

生：有關(guān)系。

生：整數(shù)是數(shù)個(gè)數(shù)，分?jǐn)?shù)是數(shù)份數(shù)。

【賞析】分?jǐn)?shù)的學(xué)習(xí)建立在整數(shù)的基礎(chǔ)上，從形式上來看，二者差別較大，但是，從內(nèi)在關(guān)聯(lián)性來看，又具有統(tǒng)一性，即整數(shù)由若干個(gè)“1”累積而來，分?jǐn)?shù)由單個(gè)的“1”均分得到。學(xué)生從幼兒園學(xué)數(shù)數(shù)開始，大量接觸了由許多“1”累加得到的整數(shù)，但是對于均分“1”得到的分?jǐn)?shù)，卻是第一次接觸。他們需要把原有的“集中思維”發(fā)散開來，逆向完成新的建構(gòu)。在這里，數(shù)學(xué)的理性表現(xiàn)為知識之間的承接性、多樣性中的統(tǒng)一性。

二、交流寫法，回顧意義，深化理解

分?jǐn)?shù)的寫法，在很多教師的課堂上是直接告知的。事實(shí)上，因?yàn)榉謹(jǐn)?shù)包含分子、分母、分?jǐn)?shù)線三個(gè)部分，學(xué)生在模仿書寫時(shí)的確出現(xiàn)了從上到下、從下往上、先中間后上下、先上下后中間等不同寫法。這里面有什么可以“玩味”的呢？許衛(wèi)兵老師非常敏銳地抓住了這個(gè)點(diǎn)。

師：1/2這個(gè)分?jǐn)?shù)你會寫嗎？請一個(gè)同學(xué)到黑板上寫一寫。（一名學(xué)生上前書寫，先寫分子1，再寫分?jǐn)?shù)線，然后寫分母2）

師：這位同學(xué)是從上往下寫的。有書寫順序不同的嗎？

生1：我是先寫2，再寫分?jǐn)?shù)線，然后寫1。

師：你是從下往上書寫的。還有不同嗎？

生2：我是先寫分?jǐn)?shù)線，然后寫2，最后寫1。

師：簡單講，就是從中間向兩邊。真是不說不知道，這一說還真奇妙。分?jǐn)?shù)的書寫到底有沒有一個(gè)大家公認(rèn)的數(shù)學(xué)順序呢？（學(xué)生你看看我，我看看你，感到十分納悶）

師：要是找不到合適的理由，那是否能舉個(gè)例子，看看1/2是怎么產(chǎn)生的。比如，一個(gè)蘋果（教師在黑板上畫一只蘋果），哪里是它的1/2？

生3：從中間把它切開。

師（在蘋果上畫一條線）：從中間切開，就是切成兩部分——同樣大，我們學(xué)過，這種分法叫做——

生：平均分。

師：也就是把這個(gè)蘋果平均分成2份（板書：平均分 ?共2份）。哪里是它的1/2？

生：其中的一份。

師：（師將其中一份畫上斜線，并板書：其中1份）這么一說，我們就明白了，要產(chǎn)生一個(gè)蘋果的1/2，首先要——

生：平均分。

師：是啊，有了平均分，才有了2份，從2份中選1份就有了1。按照這樣的過程，你們覺得寫分?jǐn)?shù)時(shí)，怎樣的順序比較好？

生4：先寫分?jǐn)?shù)線，它像平均分的線，然后寫分母2，再寫分子1。

師：這樣寫好在哪里？

生5：正好和分?jǐn)?shù)產(chǎn)生的順序一致了。

【賞析】在數(shù)學(xué)史上，分?jǐn)?shù)的書寫歷經(jīng)了豐富的過程后，逐漸變得簡約了，約定俗成了。然而，從學(xué)習(xí)的角度來看，“冰冷的美麗”背后一定有“火熱的思考”，這種思考可以和前人發(fā)現(xiàn)數(shù)學(xué)規(guī)律的經(jīng)歷一致，可以和知識的結(jié)構(gòu)脈絡(luò)一致，也可以和兒童特有的經(jīng)驗(yàn)、思維一致。但不管怎樣，都是為了學(xué)生能更好地理解數(shù)學(xué)，學(xué)好數(shù)學(xué)。上述分?jǐn)?shù)寫法的探討過程，實(shí)際上是學(xué)生對分?jǐn)?shù)意義的進(jìn)一步理解和解釋的過程。數(shù)學(xué)學(xué)習(xí)，最終是建立起學(xué)生自己的數(shù)學(xué)理解、數(shù)學(xué)認(rèn)識、數(shù)學(xué)邏輯和數(shù)學(xué)思考，為每一個(gè)理解、認(rèn)識、邏輯、思考都提供一種可行的注解，是數(shù)學(xué)理性能力的重要表現(xiàn)。

三、數(shù)形結(jié)合，手腦并用，豐富體驗(yàn)

許老師是簡約數(shù)學(xué)的倡導(dǎo)者和實(shí)踐者，他的教學(xué)簡潔、清晰、流暢、豐富而又深刻，能夠精確地把握、經(jīng)濟(jì)地妙用情景創(chuàng)設(shè)、素材選擇、活動組織、結(jié)構(gòu)安排、媒體使用等教學(xué)要素。簡潔的形式美，豐富的意蘊(yùn)美，靈動的創(chuàng)造美相互交融，渾然一體。

在研究1/2時(shí)，教師讓學(xué)生折出長方形紙的1/2。

根據(jù)學(xué)生的展示，大屏幕顯示左右對折、上下對折、斜著折三種（如圖2）。

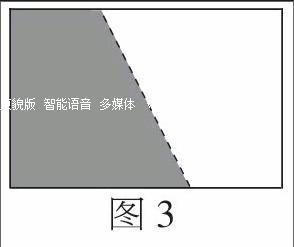
師：有沒有其他方法折出長方形的1/2？（一學(xué)生示范，如圖3所示）

師：其他人看明白了嗎？（生搖頭）看不明白正常，難度太高！剛才的三種折法，與其說有三種折法，不如說是一種方法。

（大屏幕顯示三種折法中3根折線交于一點(diǎn)，然后課件動態(tài)演示，一根折線繞點(diǎn)旋轉(zhuǎn)，將長方形通過上下、左右、對角線、任意角度都平均分成2份）

師：有多少種折法？

生1：無數(shù)種。

師：都可以用哪個(gè)分?jǐn)?shù)表示？為什么？

生2：因?yàn)槎际瞧骄殖蓛煞荩渲械囊环菥褪?/2。

師：數(shù)學(xué)就是這么有意思，已經(jīng)研究得腦子空白了，腦力不夠了，換一個(gè)角度，就有新的發(fā)現(xiàn)。

【賞析】數(shù)與形是數(shù)學(xué)研究的兩大對象，作為分?jǐn)?shù)教學(xué)的起始課，抽象思維與形象思維相互補(bǔ)充的數(shù)形結(jié)合思想，對學(xué)生認(rèn)識、理解、建構(gòu)分?jǐn)?shù)有舉足輕重的作用。許老師通過折紙環(huán)節(jié)讓學(xué)生認(rèn)識1/2、操作1/2、交流1/2，并智慧地點(diǎn)出3種折紙方法的共同交叉點(diǎn)，以不變（交叉點(diǎn)）應(yīng)萬變（無數(shù)條折痕），讓學(xué)生“跳一跳摘到果子”，萌發(fā)了好奇感，激發(fā)了學(xué)習(xí)熱情，體會到了辯證與統(tǒng)一的哲學(xué)思想和數(shù)學(xué)理性的神奇魅力。

再比如，一張紙對折產(chǎn)生1/2后，許老師讓學(xué)生再對折得出1/4、1/8，并觀察圖5，完成大小比較。

在說一個(gè)比1/8還要小的分?jǐn)?shù)時(shí)，在學(xué)生說出1/9、1/10、1/11后，許老師激勵學(xué)生說出一個(gè)“嚇人的”，學(xué)生就說出1/100、1/200、1/500。然后，讓學(xué)生聯(lián)系生活中的事例來解釋，為什么拼命把分母說得越來越大？

學(xué)生有的從折紙說起，一張紙折的等份越多，每份就越小。也有的學(xué)生舉出吃蛋糕的例子，吃一個(gè)小蛋糕，兩個(gè)人吃，一人吃一半;4個(gè)人吃，一人吃一小塊;如果分給全班吃，每人只能吃點(diǎn)兒塞牙縫;如果分給全校吃，每人舔一舔都不夠。

【賞析】學(xué)生第一次認(rèn)識分?jǐn)?shù)，教學(xué)難度并不能太大，“數(shù)不離圖”是教材編排的基本原則。但是，這并不是說教學(xué)只能停留在從圖到圖、就圖說數(shù)的淺表層次，相反，要借助于圖形直觀來孕育學(xué)生的理性思考。整節(jié)課，我都能明顯地感受到許老師的一“材”多用，一“材”巧用的匠心獨(dú)運(yùn)，在不知不覺中，學(xué)生的認(rèn)識變得豐富了，理解變得深刻了，思維變得靈活了，體驗(yàn)變得強(qiáng)烈了。

此外，本節(jié)課里，許老師還讓學(xué)生任意舉出一樣?xùn)|西，說出它的1/2，甚至于讓學(xué)生說出“許老師的1/2”，讓學(xué)生為分?jǐn)?shù)1/10畫一幅圖，等等，還滲透了數(shù)學(xué)建模的思想，而數(shù)學(xué)模型是數(shù)學(xué)基本思想的最高層次，更是數(shù)學(xué)理性思維的高級狀態(tài)。

總之，這節(jié)課因?yàn)橛辛藵鉂饫硇陨剩蔑@著數(shù)學(xué)特有的簡約之美，充滿了迷人的張力。

（責(zé)編 金 鈴）