巧用策略助力解決問題教學

陳彬燕

解決問題作為數學學習的一項重要內容，它既是培養學生應用數學能力、鍛煉數學思維的重要途徑，同時也是數學教學實踐活動中的重難點。如何切實有效地提高學生解決問題的能力，已成為小學數學教學中一個迫切需要解決的重要課題。在解決問題的教學中，為提高學生解決問題的能力，教師亟須進行一些解題策略的訓練。

一、數形結合助力理解問題表征

在數學問題的表征中，數學信息的呈現一般是將生活中的情境進行提煉和加工，去除大部分非數學的信息;學生則不然，他們需要借助生活中的經驗理解數學問題。如何化解這兩者之間的問題呢？即利用圖形將條件或問題更加直觀地展示出來，使隱藏的條件得以暴露，有利于學生了解問題的結構，明確數量之間的關系。利用圖形可以轉換問題，將學生未曾解決的問題化歸為他們所熟知的問題進行解答。在學生初次接觸“積的變化規律”后，在練習中出現這樣一道題（圖1）。如果只是讓學生讀完題目后，就直接讓他們完成，不少學生就對“寬要增加到24米”表示不理解。因此，在教學時，筆者主要引導學生借助畫圖來幫助理解題意（圖2）。

學生通過畫圖，直觀地發現這“24米”的由來，解答時也就游刃有余，學生由寬的倍數關系來解答擴大后的面積，使得學生對于“積的變化規律”有了直觀的感受，進一步深化了他們的認知。

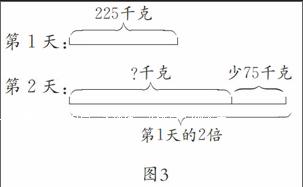
數形結合的訓練，除了直觀地畫出題意外，還可以通過線段圖或其他會意式的圖形來表示數量關系。就像到了中高年級，很多的數量關系也需要通過線段圖來理解，這會顯得更直觀、形象。就如常見的題目：副食品商店第一天賣出雞蛋225千克，第二天比第一天賣出的雞蛋的2倍少75千克，第二天賣出雞蛋多少千克？不少學生對于“比第一天賣出的雞蛋的2倍少75千克”這句話的意思不是很理解，這時如果通過線段圖（圖3），就會讓學生更形象地理解“比第一天賣出的雞蛋的2倍少75千克”這句話的意思。用圖來表示自己思考的過程，發現數量間的關系，進而理解題意，筆者覺得這對于提高學生解決問題的能力大有幫助。

二、類比練習助力區別問題模式

有些生活經驗，從表面上看，似乎與數學知識的構成沒什么直接聯系，其實不然，學生可以通過類比來幫助自己梳理相關的數學問題。學生在解決問題的過程中，常因無法在頭腦中建立合理的表象，對于相似的問題容易產生混淆，導致解答時常走入誤區。究其原因，主要是有些問題情境難以用清晰的語言進行描述，表象難以建立。因此在解決問題的教學中，類比思想的訓練必不可少，教師需針對同一內容的不同問題進行類比練習（圖4）。

此類練習，可以使學生更清晰地了解應用加減法計算的實際問題中關于數量間的變化規律，以此增進對數量關系的理解，當然，這也是要建立在充分“說圖意”的基礎上。

此外還需借助同一問題類型，但難易程度不同的內容進行類比練習。正所謂“兩刃相割，利鈍乃知;二論相定，是非乃見。”學生在一年級接觸了很多類似：“我們班有36人，15人參加興趣小組，還剩多少人沒參加興趣小組？”這樣一步解決的問題。而到了二年級，學生就馬上得接觸到兩步才能解決的問題，如：①我們班有女生17人，男生19人。15人參加興趣小組，還剩多少人沒參加興趣小組？②我們班有4組，每組9人。15人參加興趣小組，還剩多少人沒參加興趣小組？這時，教師把3道題放一起，能促使學生進一步了解復雜的數量關系的成因，才能體會數量關系在解題中的重要作用，才能讓他們在比較辨析的思維情境中，深化解題思路，發展良好的思維品質。

三、歸納練習助力問題模型的提煉

解決問題的題目千千萬，只要數字或者情境稍加改變，就會難倒一大片的學生，如何避免這樣的情形大面積出現，就需要教師在教學的過程中逐步滲透歸納的思想。就如在解決類似“媽媽買了3個碗用了18元。如果買8個同樣的碗，需要多少錢？”這種“歸一問題”題時，一般要再讓學生進行形如“小林讀一本書，3天讀了24頁。照這樣的速度，7天可以讀多少頁？”這樣的問題解答。解答后，讓學生觀察、發現解決問題中相似的地方，最后歸納出解決此類問題的共性：都要先算出一份是多少。學生經歷問題的形成、發展等一系列過程，使得他們對于“歸一、歸總”這類問題模型有了清晰的認識，這樣不管何時何地遇到相似的問題，他們也都能解決。

四、轉化策略助力靈活解決問題

其實，許多數學問題間都會有一定的聯系，利用已有的經驗和知識，將復雜的數學問題轉化為簡單的，將未知的問題轉化為已知的，將看來不能解答的問題轉化成基于已有的知識基礎的問題來解答。這樣不但可以提高學生的思維能力，也同樣可以提高他們解決問題的能力。就如探索“三角形的面積”知識時，學生一下子很難找到解決問題的方法，就要把三角形轉化成等底等高的平行四邊形去研究的。再比如，新教材將“倍的認識”放到了三上來教學，學生明確了：“a的幾倍”其實就是“表示有幾份a那么多”。后面再學習“長方形和正方形的周長”一課，當學生知道了“正方形的周長=4×邊長”后，教師就可以引導學生進行認知遷移，深入探索后發現：正方形周長與邊長之間的關系——正方形的周長是邊長的4倍，也就是說要有4份的邊長才等于正方形的周長。這樣，我們再進行變式練習“一個正方形的周長是8厘米，它的邊長多少厘米”時，學生由于知道周長與邊長之間的關系，就不容易出現求“邊長”也用“乘法”來解決這樣常識性的錯誤了。

解決問題的策略是多種多樣的，除了上文提到的，還有列表、嘗試、模仿等多種方式方法，通過這些策略讓學生主動尋求知識間的“連接點”，使學生將知識點連成線，連成面，甚至連成網，發展他們的數學思維。在這個過程中，教師是要鼓勵學生從不同的角度，用不同的思路，聯系不同的相關經驗，探索問題的多種解法，從而提高學生解決問題的能力。

（作者單位：福建省廈門外國語學校海滄附屬學校 本專輯責任編輯：王彬）endprint