常微分方程在數學建模中的有效運用研究

王復友

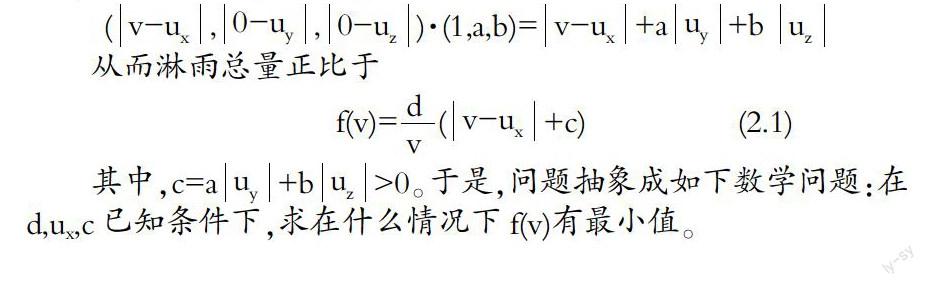
【摘要】常微分方程是17世紀隨著微積分發展起來的一種研究連續量變化的工具和解決很多實際問題與數學直接的橋梁的應用學科。牛頓證實地球公轉的軌道是橢圓形的就是通過對常微分方程進行求解得出的。海王星的發現也是科學家在解開常微分方程得出的結論，事實上確實是通過這樣發現了海王星的存在。

【關鍵詞】常微分方程 數學建模 數學模型

【中圖分類號】G42 【文獻標識碼】A 【文章編號】2095-3089（2015）04-0171-01

一、數學模型的概念

所謂的數學模型就是通過對數學工具的運用從而把實際問題和理論知識相結合，并且解釋具體的現象和情況對未來的事物發展方向進行預測，從而進行控制優化，以便更好的指導社會生活發展等。數學建模的基本流程就是：實際問題建模構建數學模型；然后對數學模型運用數學工具進行數學處理；得到處理后的數學模型的解；通過對數學模型的解加以闡述和解釋來得出實際問題的解；最后通過實際問題的解回歸到實際問題中加以預測或者解決問題。所以，數學模型其實就是通過數學工具或者數學語言對實際問題的一個概況描述。主要目的就是為了解決實際問題。

二、數學建模的方法

第一步準備模型，首先是對想要建模的實際問題進行了解，確定建模目的，弄清建模的內容方向，然后通過計算機或者在圖書館查閱相關信息，然后對問題進行總結分析，進行深入研究調查。

第二步是通過對模型的深入調查研究以后，對問題進行化繁為簡，抓住問題的主要因素，把次要的不影響大的結果的因素忽略簡化，進而對模型提出假設構想，然后不斷的進行修改和完善。

第三步是在模型假設的基礎上，選擇正確的合理的科學的數學工具對實際問題的變量進行描述，要注意分清變量的類型，正確選擇合適的數學工具建立微分方程。要盡可能的把握問題的本質，簡化掉多余的信息，進行嚴密周祥的推理，同時要保證思路清晰、明了盡量提高準確性，科學性。

第四步是在上面的基礎上，運用對微分方程的求解來解釋具體問題。

第五步是在得到模型的解以后，對它進行分析檢驗，然后與實際情況結合比較，如果結果誤差小，說明模型是成功的，反之要對模型進行修改再重復上面的步驟，一直到正確的模型得到正確的解。

最后是把上面得到的模型的解，運用到實際問題中，進行預測分析。一般情況下，建模可以對事物發展進行預測，而預測可以為決策者決策控制提供有效的信息。

四、常微分方程在數學建模中的運用

上文已經對數學建模的過程進行了簡單概述，以及模型的分類。現在以實際實例來說明常微分方程在數學建模中的實際應用。

人們日常生活中外出時難免碰到下雨卻沒有帶傘的情況，怎么樣才能少淋雨是一個問題。我們就怎么減少淋雨程度進行研究。

模型假設：通過描述可以知道主要因素有：雨的大小，方向以及人走路的路程和速度。為了建立模型我們提出這樣的假設：1把人當做長方體，頂，側、前的面積比是b：a：1；雨中某地直線距離d，風速和雨速都不變，建立一個直角坐標系（V，0，0），設雨速（ux，uy，uz）：

在上述假設下，由高等數學中曲面積分的通量概念，顯然，單位時間內的淋雨量正比于

3.當ux=c及ux>0，分別為式（2.1）和式（2.2）的特例。

綜上所述，當ux>c>0時，只要v=ux就可使前后不淋雨，從而總雨量最小。

除此之外都應盡可能的使v最大，所以只有跑得快，才會淋雨少。

五、結束語

綜上所述，常微分方程在數學建模的運用是一個長期細致系統性的工程，通過教學實踐發現常微分方程在數學建模中的運用可以大大提高學生的學習積極性和對數學知識的運用。在今后的教學中，應該在現有的基礎上繼續對數學建模和常微分的結合使用進行深入探究，更好的引入常微分方程在數學建模中的運用，以便提高教學質量。

參考文獻：

[1]韋程東，高揚，陳志強等.在常微分方程教學中融入數學建模思想的探索與實踐[J].數學的實踐與認識，2008，38（20）：228-233.