小改變大不同

余亞明

[摘 要] 變式教學對提高學生的學習積極性，拓寬學生的思維空間，提高教育教學水平有一定的幫助，本文從三個方面舉例說明“變式教學”的優(yōu)勢：變式教學幫助學生理解新知；變式教學利于學生解決問題；變式教學促進學生學會變通.

[關(guān)鍵詞] 變式教學；方法；優(yōu)勢

變式教學就是對數(shù)學中的例、習題進行不同背景、不同情形、不同角度、不同層次的變式，從而暴露問題的本質(zhì)，揭示相關(guān)知識間內(nèi)在聯(lián)系的一種教學方法. 通過變式教學，可使學生觸類旁通，達到一題多用、一法多用、多題一解、多題歸一的效果，從而提高學生的學習積極性，拓寬學生的思維空間，提高教育教學水平，下面結(jié)合課堂教學實踐從三個方面舉例說明“變式教學”的優(yōu)勢.

變式教學幫助學生理解新知

學生在剛接觸一個新的數(shù)學概念時，很容易只停留在知識的表層，通常難以理解概念的內(nèi)涵和外延. 所以在新概念形成過程中要多方面呈現(xiàn)概念的外延并接觸一些“貌合神離”的情形，以便突出概念的內(nèi)涵，這樣能幫助學生正確、深刻地理解新知并掌握新知.

例1 學習一次函數(shù)時，在學生了解了“形如y=kx+b（k、b是常數(shù)，k≠0）的函數(shù)是一次函數(shù)”的概念并讓學生對幾個簡單的函數(shù)解析式進行辨別后，可以設(shè)計這樣的變式訓練：

學生在解決變式4和變式5時出錯率很高，他們把（m2-4）xm錯誤理解成最高次項，這時教師在學生出錯的基礎(chǔ)上適當點撥，（m2-4）xm的次數(shù)可以高于一次，得出m2-4=0；（m2-4）xm的次數(shù)可以是一次，得出m=1；（m2-4）xm的次數(shù)也可以是零次，得出m=0. 變式4共有三種答案，變式5在變式4的基礎(chǔ)上要考慮系數(shù)m-2.學生聽完講解恍然大悟，理解了自己出錯的真正原因，加深了對概念的理解，這樣由表及里，由淺入深，層層深入，環(huán)環(huán)緊扣，給學生清晰的層次感，從層層遞進的變式中激活學生的思維，同時使學生的思維有了深度和廣度，更讓學生學會了知識的遷移.

變式教學利于學生解決問題

很多學生在解題時，一旦遇上把題目條件或圖形結(jié)構(gòu)做少許改變的題目，就會感到無從下手. 其實這些變了的題目與原題在知識、方法上是有關(guān)聯(lián)的，只要引導學生對這些題目進行類比，歸納解決它們的常見方法及數(shù)學思想，就能達到解一題、融一類、會一片的境地，從而提高學生的解題能力.

在平行四邊形的判定定理3的教學時，可以這樣設(shè)置一組變式題目：

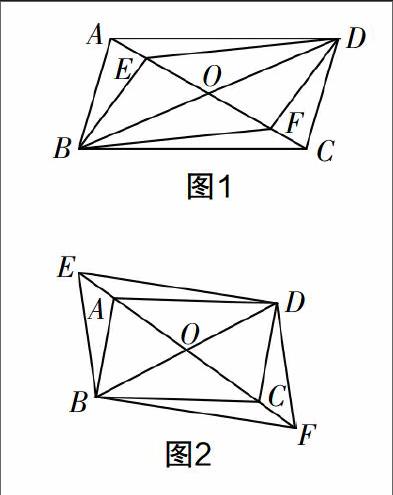
例2 如圖1，？荀ABCD的對角線AC，BD相交于點O，E，F(xiàn)是AC上的兩點，并且AE=CF，求證：四邊形BFDE是平行四邊形. （新人教版數(shù)學八年級下冊教科書46頁例3）

教科書主要是利用“對角線互相平分的四邊形是平行四邊形”這個判定定理來證明四邊形BFDE是平行四邊形.

變式1 如圖2所示，若將例題中的已知條件E，F(xiàn)是AC上的兩點，改為點E，F(xiàn)在AC兩側(cè)的延長線上，其他條件不變，四邊形BFDE是平行四邊形嗎？為什么？

雖然點E，F(xiàn)位置改變但引導學生抓住實質(zhì)，利用等式性質(zhì)仍能證出OB=OD，OE=OF，還可以利用例題的判定方法.

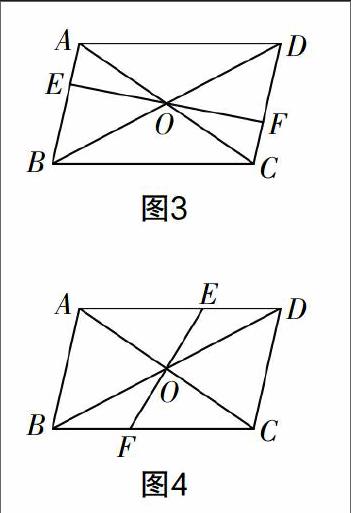
變式2 如圖3、4所示，？荀ABCD的對角線AC，BD相交于點O，直線EF經(jīng)過點O與？荀ABCD的對邊分別交于點E，F(xiàn)，四邊形BFDE還是平行四邊形嗎？為什么？

這時，點E，F(xiàn)的位置到了平行四邊形的邊上，有了前兩題作為鋪墊，不管是圖3還是圖4，學生很容易聯(lián)想到證OB=OD，OE=OF，從而證到結(jié)論. 加深了學生對判定定理的理解，又培養(yǎng)了學生思維的發(fā)散性.

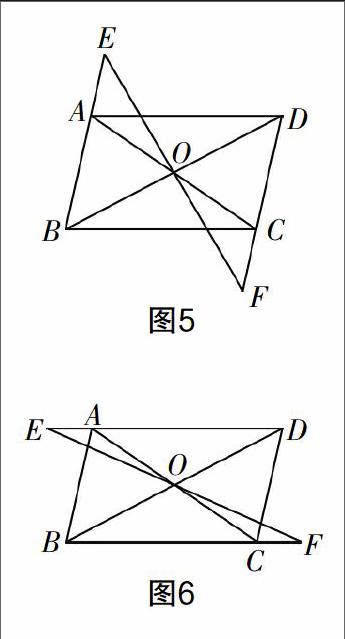
變式3 如圖5、6，？荀ABCD的對角線AC，BD相交于點O，直線EF經(jīng)過點O與？荀ABCD的對邊所在的直線分別交于點E，F(xiàn)，四邊形BFDE還是平行四邊形嗎？為什么？

變式3在變式2的基礎(chǔ)上進一步加深，由點E，F(xiàn)的位置在線段上變?yōu)樵谥本€上，范圍擴大，教學時可以在前面圖形的基礎(chǔ)上讓學生自己畫出滿足條件的圖形加以探究，發(fā)現(xiàn)此問題仍然可以利用例題的判定方法得出相同的結(jié)論. 通過變式3的訓練可以加深對判定的靈活應用，充分培養(yǎng)學生的解決問題的能力和探究能力.

變式教學促進學生學會變通

教學中經(jīng)常遇到這樣的情形：學生對所學知識點掌握較好，也形成了一定的解題經(jīng)驗，但容易產(chǎn)生思維定式，一旦遇到變通就束手無策. 因此，教學中不能墨守成規(guī)，要注重對比分析，滲透變通意識.

例3 如圖7，菱形ABCD的對角線長分別為6和8，點M，N分別是邊AB，BC的中點，點P是對角線AC上的一個動點，求PM+PN的最小值.

這是一道典型的動點最值問題，其特征是一動兩定型，即一個動點（點P），兩個定點（點M，N）. 采用對稱共線法，利用軸對稱變換，如圖8，將線路中線段PM，PN映射到同一直線上（線路長度不變），從而確定動點P的位置，并計算線路最短長度，也就是MN′的長度5.

變式 如圖7，菱形ABCD的對角線長分別為6和8，N是邊BC的中點，點M、點P分別是邊AB、對角線AC上的一個動點，求PM+PN的最小值.

變式中，M點已經(jīng)變?yōu)閯狱c，其特征是兩動一定型，即兩個動點（點M，P），一個定點（點N），所以P點的確定與例題大不相同，這時引導學生思考：

（1）M點還一定是AB的中點嗎？

（2）線段PM，PN如何映射到同一直線上？

（3）如何讓線路長度最短？

通過思考，啟發(fā)學生對比聯(lián)系變式與例題之間的聯(lián)系和區(qū)別，學生能順利地利用軸對稱變換及“垂線段最短”的知識確定出動點P的位置，如圖9，計算出線路的最短長度，也就是MN′（菱形的高）的長度4.8.

例4 如圖10，在？荀ABCD中，AD=2AB，F(xiàn)是AD的中點，作CE⊥AB，垂足E在線段AB上，連接EF，CF，則下列結(jié)論中一定成立的是______. （把所有正確結(jié)論的序號都填在橫線上）

變式 如圖12，教師可從以下角度對學生進行點撥，取BC的中點G，連接FG，交EC于點H，可得四邊形FGCD是菱形，則①輕松得出；再連接EG，易得GE=GC，又GH⊥EC，故FH垂直平分EC，則②④就能隨之得出了；因為S△BEC=2S△CEG，而S△CEF 不一定等于S△CEG，故③不成立.

變則通，通則靈，靈則活，這樣的變式訓練開闊了學生的解題思路，能使學生從單一的思維模式中解放出來，有利于將知識、能力和思想方法用于更多的新情景、更高的層次中，通過不斷地反復滲透，從而達到對知識螺旋式的再認識，再深化，乃至升華的效果.

以上是筆者在教學實踐中的一點嘗試，當然，變式教學中的變式訓練不是為了“變式”而變式，而是要根據(jù)學生的學情，遵循學生的認知規(guī)律而設(shè)計，其目的是通過變式訓練，使學生在理解知識的基礎(chǔ)上，把學到的知識轉(zhuǎn)化為能力，形成技能和技巧，完成“應用—理解—形成技能—培養(yǎng)能力”的認知過程. 因此，教學中數(shù)學變式訓練設(shè)計要巧，要有一定的藝術(shù)性，要正確把握變式的度，要有目的性，要起到引導、激發(fā)學生思維活動的作用.

總之，數(shù)學教學中變式教學是對學生進行數(shù)學技能和思維訓練的重要方式，它能有效地培養(yǎng)學生思維的深刻性、開闊性、發(fā)散性、靈活性和獨創(chuàng)性. 因此，在數(shù)學教學中我們要善于利用變式教學，激活學生思維，提高課堂教學的有效性.endprint