探究小車速度隨時間變化規律實驗中的紙帶處理問題
張毅敏
(蘇州大學科學與技術學院 江蘇 蘇州 215006;蘇州第十中學 江蘇 蘇州 215006)
“探究小車速度隨時間變化規律”的實驗中紙帶的處理問題是高中物理實驗的一個重要內容,也是高考實驗考查的重點,但筆者發現在實際教學中學生掌握起來有頗多障礙,他們在處理數據時往往只是依葫蘆畫瓢,未能真正掌握要領學會靈活運用.現將紙帶處理中遇到的問題歸納、分析如下.
1 如何選取紙帶
需要多次實驗打下幾條紙帶,然后選取其中一條理想的紙帶進行研究.選取紙帶的原則是:打點清晰,無漏點,無拖尾.如果紙帶上打下的點不是圓點而是一些短線,這可能是因為振針壓得過緊導致在紙帶上拖動造成的,這樣的紙帶就不能選.
2 如何標注計數點
打點計時器在紙帶上打下的點叫實驗點,在處理數據時,為了測量方便和減小誤差,通常要舍掉開頭一些比較密集的點,從看得清的某個點開始每隔幾個實驗點標注一個計數點.這樣做是因為紙帶開頭的點過于密集不便測量,而且物體開始運動與打點計時器開始打點往往不同步,第一個點的位置不易辨別.
3 如何確定計數點間的時間間隔
打點計時器使用的交流電源的頻率為50 Hz,因此每隔0.02s打下一個點,也就是說紙帶上相鄰實驗點間的時間間隔為0.02s,但由于計數點與實驗點的區別,相鄰兩個計數點間的時間間隔就并非0.02s.為了測量方便和減小誤差,計數點間距要盡可能大,通常每隔4個點取一個計數點,即相鄰計數點間的時間間隔為t=5×0.02s=0.1s.值得注意的是有時表達方式不同但代表的含義卻相同,比如實驗考題中有時會直接告知相鄰兩計數點間的時間間隔為0.1s;或表述成:在紙帶上便于測量的地方選取第一個計數點,在這點下標明A,第6個點下標明B,第11個點下標明C……;也可說成:從0點開始,每5個點取一個計數點或每兩個相鄰的計數點之間還有4個點沒有畫出,這些都表示相鄰計數點間的時間間隔為0.1s.
4 如何測量計數點間距離
測量相鄰兩計數點間距離時不要分段測量,而是要用長刻度尺對齊各計數點不移動尺子一次性讀出計數起點到其他各計數點間的距離,然后通過計算得到相鄰兩計數點間長度,這樣可以避免測量誤差的積累.例 如 圖1 中 先 直 接 測 量s1,s2,s3,s4,s5,s6,再通過計算得

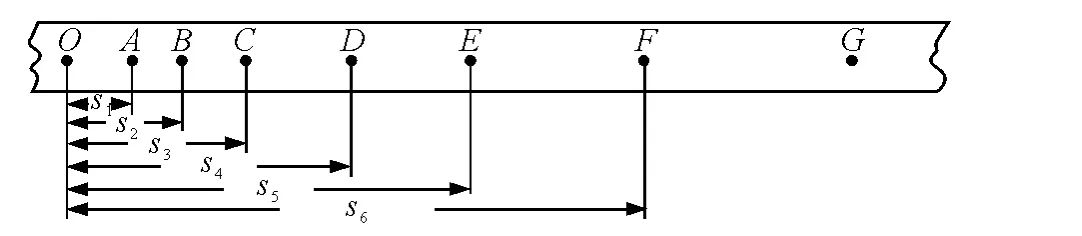
圖1
5 如何求瞬時速度
物體做勻變速直線運動時,測定某點的瞬時速度可根據“某段時間內的平均速度等于這段時間內中間時刻的瞬時速度”來求,即測出該點前后兩段相等時間T內的距離,由平均速度公式就可求得,如求圖1中B 點的速度為
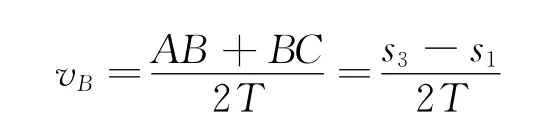
在這里筆者想說明的是,在處理高中《物理·必修1》第一章第4節“用打點計時器測速度”實驗時并非一定要用這個原理來測定某點的瞬時速度,也可用求出該點前一段很短時間內的平均速度或該點后一段很短時間內的平均速度的方法來求得,因為當時間足夠短Δt→0時,可認為瞬時速度等于平均速度,如圖1中各點均為打點計時器打下的實驗點,則物體在B 點的速度

6 如何求加速度
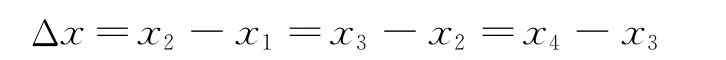
這就是一組理想數據,利用任意一段位移減去前一段位移代入公式即可.但事實上由于實驗的誤差Δx往往有很多組解,如果只利用其中一個Δx 求得的加速度偶然誤差太大,最好多次測量求平均值,于是就有
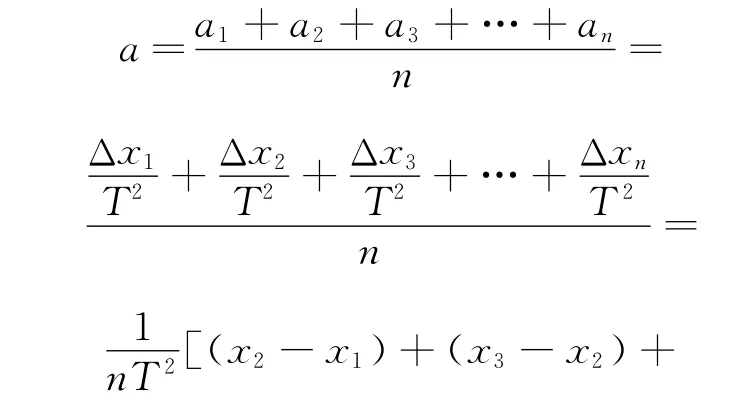
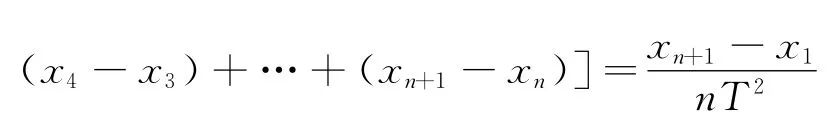
這樣的結果只由xn+1和x1決定,偶然誤差很大.如何把紙帶上各段位移都利用起來?通常我們用的方法是“逐差法”,即
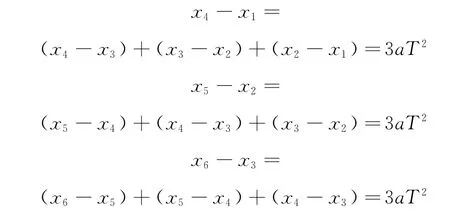
所以
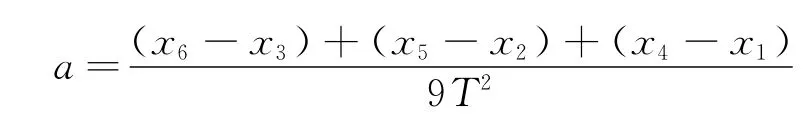
這樣就把各段位移都利用上了,有效地減小了僅由兩次位移測量帶來的偶然誤差.但這種方法學生往往難以理解與記憶,筆者認為不妨把“逐差法”變為“兩段法”,即
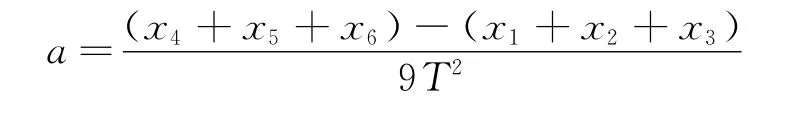
這樣在測量時只需將打點紙帶分成兩大段來處理,便于學生理解和掌握,且測量時減少了誤差,記憶與運算也較為簡便.如果打點紙帶為奇數段,則需舍掉第一段或最后一段,剩下來的偶數段用“兩段法”處理即可.
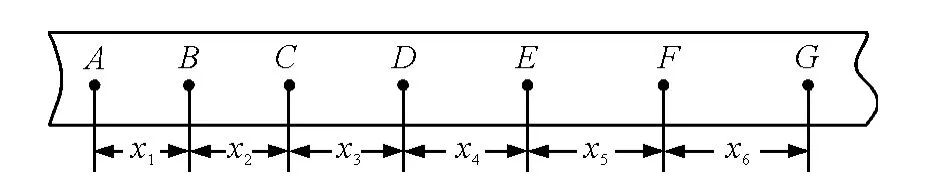
圖2
7 如何求第一個計數點和最后一個計數點的速度
利用勻變速直線運動的速度公式v=v0+at即可求出,但要注意的是第一個計數點不一定是真正打下的第一個實驗點,所以它的速度不一定為零.
隨著近幾年新課程改革的不斷深入,在未來高考命題中會有更多的有關紙帶數據處理的創新型命題出現,這就要求學生從基礎抓起,真正理解實驗原理并能靈活運用.

