培養學生在復習課中的探究——在全等三角形復習課中的啟發

浙江省樂清市大荊鎮第一中學 徐才君

探究能力是一種十分重要的能力，如何對學生進行探究能力的培養一直是許多教師探索的課題，而本文通過在一節觀摩教學中收集的教學案例片段，對案例進行評析和反思，探索在復習課的教學中如何更有效地培養學生的探究能力.

案例 探究三角形全等的應用

片段一

多媒體顯示教師提出的問題，小明有塊等腰三角形形狀的三角板，AB=AC，你能把它分成兩個全等的三角形嗎？如能，趕快行動.

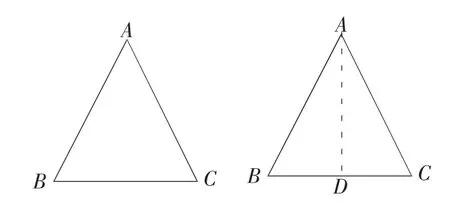
教師：大家思考用怎樣的方法？

學生思考.

教師：仔細想一想，并把推理過程寫出來，并思考有無第二三種方法.

學生踴躍舉手.

教師：我們來看一下一些同學的解法.

同學甲：作∠BAC的平分線AD，用SAS說明.

同學乙：作∠BAC的高AD，用AAS或ASA說明.

同學丙：作∠BAC的底邊BC上的中線AD，用SAS說明.

教師：這幾位同學做得都很好，用到判定全等三角形的方法：AAS，ASA，SAS，有沒有其他方法？大家討論一下，并與自己的方法比較一番.

同學丁：還有，仍然作中線AD，但可用SSS來說明全等.

教師：補充得很好，此題四種說明全等的方法都可以用.

[評析] 這與以往習慣上教師先復習說明全等的四種方法，再解題截然不同，先提出一個問題，讓學生自己從各個不同的角度去解決，補充，既復習了整個知識體系，又達到了知識的靈活應用，培養了解決實際問題的能力，在這個過程中，學生的思維是發散的，全體學生都能積極、主動地參與到“探索學習”的過程中來，給了學生盡可能多的獨立思考的時間，以及合作交流的機會.

片段二

教師顯示例題：小明做了一個如圖所示的風箏，其中 ED=DF，EH=HF，如右圖所示，小明不用測量就能知道∠EDH=∠FDH，為什么？

學生：△EDH與△FDH全等，所以∠EDH=∠FDH.

教師：怎么判定？

學生：SSS.

教師：很好，那么大家也不用測量，還能知道這個圖中其他結論嗎？

學生踴躍舉手，思維活躍.

教師：我偏叫不舉手的同學回答.（學生笑）

一位未舉手的男生：∠EHD=∠FHD，∠HED=∠HFD.

教師：好極了！原來你很聰明.

學生：圖中還有許多相等的邊角，一下子數不完.

教師：嗯，既然有那么多，那么我們何不歸類？如考慮哪些三角形全等？

學生：三對，它們是△EDH≌△FDH，△EDO≌△FDO，△EOH≌△FOH.

教師：那么相等的邊，相等的角也都解決了，還有其他結論嗎？比如從位置關系考慮.

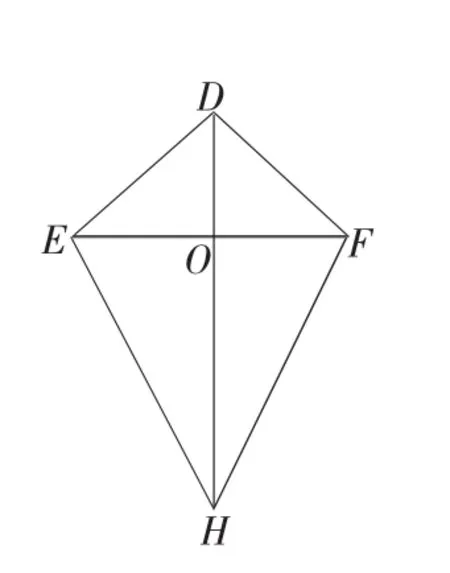
學生思考

學生：DH⊥EF.

教師：怎么知道的？

學生：∠HOE=∠HOF，當然等于90°了.

教師：很好，也就是DH是EF的中垂線，那么EF是否是DH的中垂線？

學生甲：是的.

學生乙：不是.

教師：大家討論一下，認為“是的”同學思考怎么說明，認為“不是”的同學想一想.

學生思考討論

教師：在什么情況下結論成立？

學生討論激烈，幾分鐘后，學生出色地回答了這個問題.

[評析] 此例題讓學生親身感受到數學來源于生活又服務于生活.讓學生用已有的知識經驗一下子解決了第一個問題，使學生體會到成功時的喜悅，感受到學習數學的樂趣，這樣的課堂教學激發了學生學習數學的積極性和情感體驗，使學生很輕松地進入第二個問題的解決.小結理順學生的思路，從而探究出了更多的新成果，進一步提高了學生的探究能力.

片段三

多媒體顯示問題：

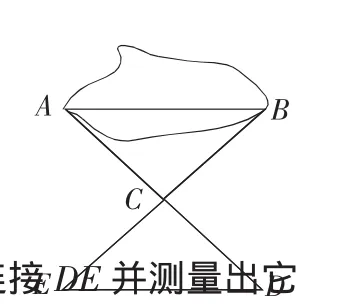
如圖，A，B兩點分別位于一個池塘的兩端，小明想用繩子測量A，B間的距離，但池塘里種了好多蘆葦，不可直接測量，一個叔叔幫他出了這樣一個主意，先在一片空地上取一個可以直接到達A點和B點的點C，連接AC并延長到D，使CD=AC；連接BC并延長到E使C E=C B；連接并測量出它的長度，DE的長度就是A，B間的距離.你能說明其中的道理嗎？

教師：此題題目較長，題中包含什么已知條件，要說明什么結論？

學生思考，分組討論.

學生：題目的意思就是兩個三角形中，已知 AC=CD，BC=CE，說明 DE=AB.

教師：說得很好，那么長的題目你能弄清題意，真是不錯，大家都明白意思了嗎？

學生：明白了.

教師：如何說明？

學生：兩個三角形全等.因為還有一個角相等，即∠ACB=∠DCE，利用SAS來說明.

教師；非常聰明，下面我們再仔細看一下題意，因為AB是不能直接測量的，DE的長能用繩子測量嗎？

學生：能測，因為在空地上.

教師：對。那么大家也想一想有沒有其他方法呢？

大家思考，通過各個小組討論后，學生舉手發言.

學生：在AB的過點A的垂線上取一點C，連接BC并延長到D，使BC=CD，畫DE⊥AE，并使A，C，E在同一條直線上，這時測量出DE的長就是A，B間的距離.

[評析] 教師就地取材及時對學生進行思想教育，幫助學生樹立信心，培養了學生解題意志.

反思

如何設計恰到好處的探索性問題，所設計的問題必須建立在學生已有的認識基礎上，并且能體現復習的知識體系，以及能提示各知識要點的本質內涵，所以這一類探索性問題的設計既不能高深莫測，不然會使大部分學生沒有方向，無法下手，又不能平淡無味，否則會失去探索的意義，教師盡可能選擇源于現實生活的問題，能融生活趣味和知識趣味于一體的問題，激發學生興趣，引發他們積極思考，通過對問題的探討，解決，從中既能復習舊知識體系，又能發現數學思想和方法，更能促進學生在以后遇到相關問題時就能自覺地運用有關的數學經驗去思考，解決問題，達到“講一題，明一類”.

[1]羅永高.研究性學習課題教學“渡河問題”的教學設計.數學通訊2004.1

[2]張玉敏.數學教學中的合作學習小組.中學數學參考2003.1