基于HHT法的流化床內生物質和石英砂雙組分顆粒 壓差脈動信號分析

趙凱，仲兆平，王肖祎，王澤宇

（東南大學能源與環境學院，能源熱轉換及其過程測控教育部重點實驗室，江蘇 南京 210096）

引 言

生物質能作為一種新能源，已經得到社會的廣泛關注。目前，流化床內生物質的熱解氣化是利用生物質能源化轉換的重要技術。但由于生物質本身密度小、形狀不規則等特點，在流化床內很難單獨流化，必須有流化介質（如石英砂），這樣既可以提高生物質熱解氣化的溫度，也可以改善流化床內生物質單獨流化的流化特性。

壓差脈動信號承載著流化床內氣固流動狀態的大量信息，為進一步分析流化床內氣固兩相流動特性提供重要的依據。早期處理壓差脈動信號的方法主要包括短時傅里葉變換、Wigner-Ville 分布、小波變換、遞歸分析、復雜性分析[1-6]等。Huang 等[7]于1998年創立了一種新的基于時間序列的分析方法，即Hilbert-Huang 變換（HHT）。Hilbert-Huang分析方法具有自適應性的特點，通過經驗模態分解法（EMD）有規律地將原始信號分解為有限個具有一定特征的內稟模態函數（IMF），目前很多學者采用此方法對流化床內的流動特征進行研究。王曉萍[8]采用HHT 方法分析了流化床內氣固壓力脈動信號流動特性，發現各階IMF 中頻能量轉換與流化床的流動狀態有很好的對應關系，提出了基于HHT 流型識別的新方法。黃海等[9]對氣固壓力脈動信號進行Hilbert-Huang 譜分析，研究顆粒結塊對IMF 能量分布的影響，指出顆粒結塊敏感地改變IMF 能量的分布規律，為判斷流化床內顆粒結塊故障提供了新思路。周云龍等[10]采用HHT 和Elman 神經網絡方法對氣液兩相流進行流動特性分析，得出EMD分解方法的優越性和IMF 的能量變化能夠很好地識別水平管道內不同流型的結論。Wang 等[11]采用HHT 方法對噴動流化床內壓力脈動信號進行分析，通過提取內稟模態函數的特征參數發現固定床狀態、噴動流化狀態、鼓泡流化狀態、騰涌流化狀態的識別率分別可以達到90%、85%、85%、95%。Ding 等[12]對水平管內氣固兩相流壓差脈動信號進行HHT 分析，發現了隨水平管道內流型的轉變高、中、低頻段能量轉移的一般規律，同時也證明HHT方法適用于分析非線性、非平穩的氣固兩相流信號。Lu 等[13]通過對高壓下氣固兩相流Hilbert-Huang 譜分析發現由Hilbert-Huang 譜提取的能量特征能夠反映出能量隨流型改變轉移。Rai 等[14]通過將基于頻率域IMF 的快速傅里葉變換與Hilbert 變換相合并的方法對軸承振動信號進行分析，得出HHT 變換頻率域分析的有效性，證明這種方法最適合應用在軸承故障診斷方面。Or-ampai 等[15]通過對流化床內不同流型下的壓力脈動信號的功率譜分析得出功率譜有一個寬泛的頻率范圍，主要集中在0～4 Hz，而且頻寬會隨固體密度的減小而減小的結論。目前Hilbert-Huang 變換還在海洋、生物工程、地震、橋梁健康監測、噪聲分析[16-19]等領域得到廣泛應用。

關于木桿與石英砂雙組分顆粒混合流動特性的研究[20]相對較少。本研究主要通過Hilbert-Huang變換方法對流化床內生物質和石英砂顆粒壓差脈動信號進行分析，研究不同氣速和不同生物質含量下的生物質與石英砂的混合流動狀態，這對未來生物質在流化床內熱解和氣化的研究具有重要意義。

1 Hilbert-Huang 變換原理

HHT 時頻分析方法主要由經驗模態分解（empirical mode decomposition，EMD）方法和Hilbert 變換（Hilbert transform，HT）兩部分內容組成，其中EMD 方法是HHT 的核心部分。EMD 自適應地將原始信號按頻率從高到低順序分解為固有模態函數（intrinsic mode function，IMF），而IMF簡單相加便還原為原始信號。

由EMD 分解出來的固有模態函數(IMF)必須滿足以下兩個條件[21]：①每個IMF 的極值點的個數與零點數必須保持相等或者至多相差一個；②每個IMF 極大值點相連的上包絡線與極小值點相連的下包絡線的均值必須等于0，即IMF 的對稱性。

假設原始信號為x(t)，對x(t)進行EMD 分解，具體分解方法見文獻[21]，得到有限個固有模態函數（IMF）與一個殘余量，分別表示為ci(t)和r(t)（其中i=1,2,3,…），原始信號可重新表示為

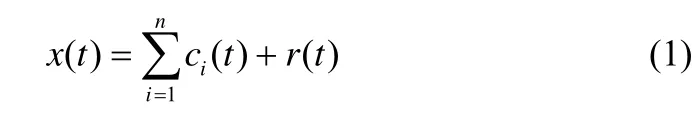
每個IMF 的瞬時頻率和幅值可以通過對IMF 進行Hilbert 變換得到，表示為di(t)

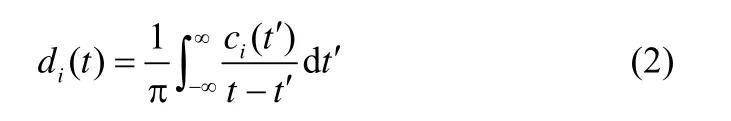
由此得到對每個IMF 進行Hilbert-Huang 變換的解析信號，表示為zi(t)

由解析信號得到每個IMF 的幅值函數和相位函數，分別表示為ai(t)、φi(t)

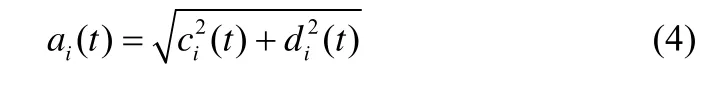
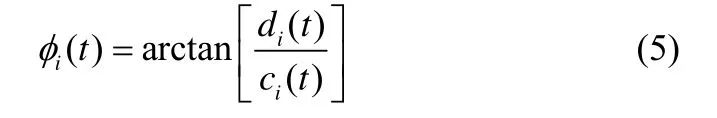
最后根據相位與順時頻率的關系（某一時刻相位的導數等于瞬時頻率）得出每個IMF 的瞬時頻率，表示為fi(t)

每個IMF 可表示為關于瞬時頻率和幅值的函數形式，即Hilbert 譜

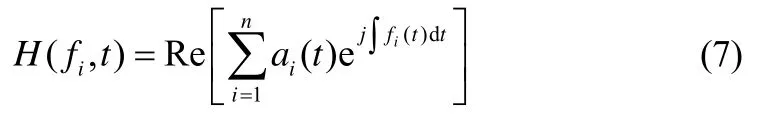
Hilbert 譜描述了瞬時頻率與幅值隨時間的變化規律，式(7)中Re 表示取實部。

用Hilbert 譜定義HHT 中的邊際譜

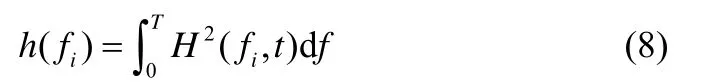
由振幅的平方對頻率積分，可以定義為瞬時能量

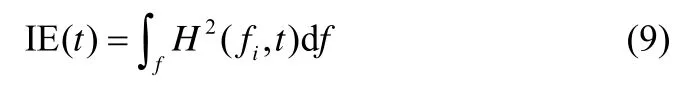
2 實驗裝置與方案

2.1 實驗裝置

實驗裝置主要由動力系統、流化床、檢測系統構成，其中動力系統包括鼓風機和轉子流量計。流化床主體所用材料是6 mm 厚的有機玻璃，長寬高分別為120、32、1000 mm；布風板厚度為6 mm，上面有100 個孔徑為1.5 mm 的小孔，開孔率為3%，采用等邊三角形錯列方式排列。考慮到測壓孔應該布置在流化床中心和流態化發展比較充分的地方，以便測量不同床高下的壓差脈動信號，在床體一側距布風板200、300 和400 mm 處開3 個直徑為8 mm的測壓孔。檢測系統包括計算機、USB 數據采集器（RBH8251-13 型）和壓力傳感器（KMSSTO 型，量程0～35 kPa），測量精度為0.1 級，高速攝影儀（Photron SA4，分辨率像素1024×512，最高每秒12500 幅的記錄速度，本實驗拍攝頻率為1000 Hz）。實驗裝置如圖1所示。

2.2 實驗方案

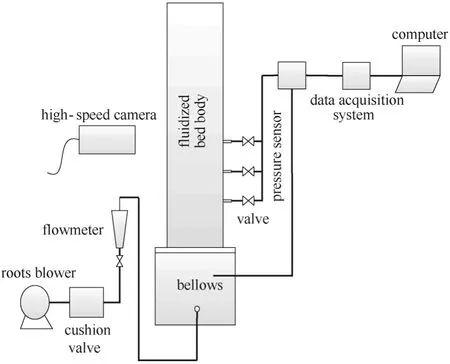
圖1 實驗裝置Fig.1 Schematic diagram of experimental setup

本實驗選取粒徑為0.4mm 的石英砂顆粒和直徑不同（直徑×長度分別為4 mm×10 mm、6 mm× 10 mm、8 mm×10 mm、10 mm×10 mm）的柱形木桿顆粒作為床料。實驗所用的流化介質為常溫下的空氣，由羅茨風機提供。采樣頻率選擇f=100 Hz，每次采樣時間為15 s。為保證采樣的準確性，避免外界因素的可能性干擾，每種工況下重復采樣3 次。實驗工況：木桿和石英砂混合后靜止床高為150 mm，表觀氣速為0.29～2.31 m·s-1，木桿質量分數w分別為0、2%、4%、6%、8%。表1給出了實驗中的顆粒特性。

3 實驗結果與分析

3.1 臨界流化風速

圖2為生物質質量分數分別為2%、4%、6%、8%時平均壓差（Δp）隨氣速變化的曲線。從圖中可以看出，隨著氣速的變化，不同的生物質含量對應的平均壓差均呈現先快速增加后相對平穩的整體趨勢。而隨著生物質含量的增加，平均壓差逐漸下降，生物質質量分數為2%、4%和6%時平均壓差相差不大，生物質質量分數為8%時平均壓差下降較為明顯。其主要原因是，由于生物質密度比石英砂密度小很多，隨著生物質質量分數增加，整個床料的平均堆積密度下降，導致氣體流過床料的阻力減小，而平均壓差是指流化床主體下端的氣體入口與測壓孔之間的平均壓力差，當床料的阻力下降時，系統的平均壓差自然而然地隨之減小。當生物質質量分數為8%時，生物質顆粒明顯增多，平均堆積密度下降比較明顯，因此平均壓差下降較快。采用壓降法可以測得不同生物質含量下的臨界流化風速大約為v=0.45 m·s-1。

表1 實驗中的顆粒特性Table 1 Particle characteristics in experiment

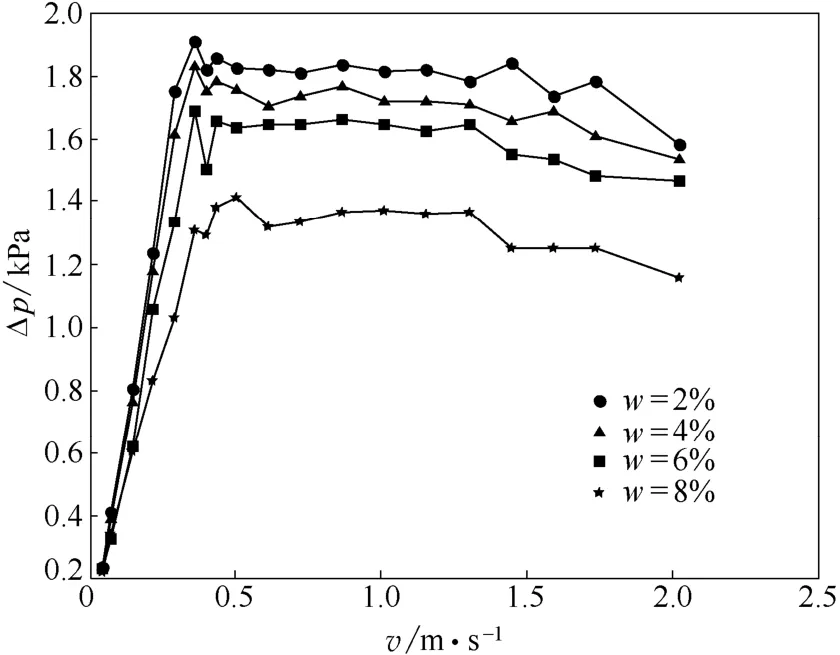
圖2 不同生物質含量下平均壓差隨氣速的變化曲線Fig.2 Curve of average pressure differential at different gas velocity with different biomass proportion

3.2 壓差脈動信號的邊際譜分析

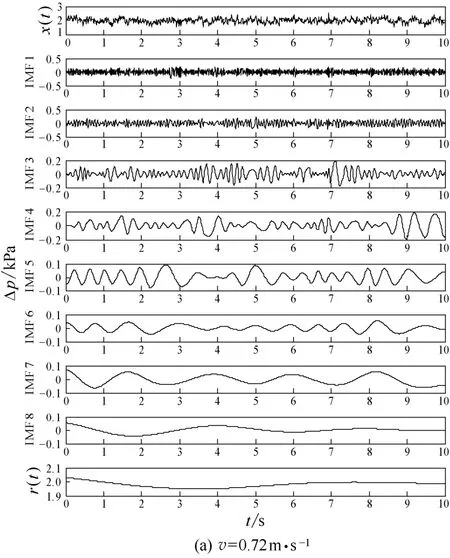
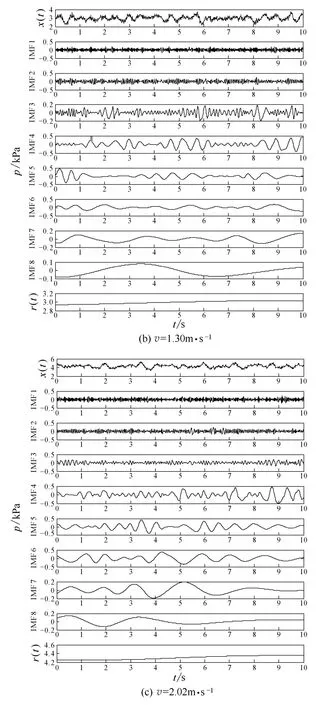
圖3 w=2%時不同氣速下壓差脈動信號的IMF 圖Fig.3 IMFs of pressure fluctuation signal under different gas velocity when w=2%

為保證壓差脈動信號原始圖像的準確性，在選取數據時應盡量選取床料流化穩定后的數據，以避免EMD 分解過程中邊緣效應[22]帶來的影響。圖3是生物質質量分數為2%，氣速分別為0.72、1.30和2.02 m·s-1時壓力脈動信號的IMF 圖。圖中x(t)為原始信號，利用EMD 分解方法將原始信號從高頻到低頻分解為8 個內稟模態函數（IMF）和1 個 殘余分量r(t)。將分解的8 個IMF 分為3 個頻段，高頻部分為IMF 1～3，中頻部分為IMF 4～6，低頻部分為IMF 7～8。由式（7）可知，圖3中(a)、(b)、(c)各階IMF 分量均具有調幅和調頻形式。流化床內氣泡的聚并、上升、破裂引起粒子之間的相互碰撞沖擊，導致壓差脈動信號既具有波間調制又具有波內調制，表現為信號的非線性性質。另外，隨著氣速的增加，圖3中(a)、(b)、(c)原始信號的幅值越來越大，其主要原因是由于氣量增加，流過流化床內的氣速增大，進而流化床入口壓力增大，而生物質質量分數為2%時所對應的流動阻力是基本不變的，從而導致流化床入口和測壓口的壓力差隨氣速增加越來越大，圖3中體現為原始信號的幅值隨氣速增加而變大。

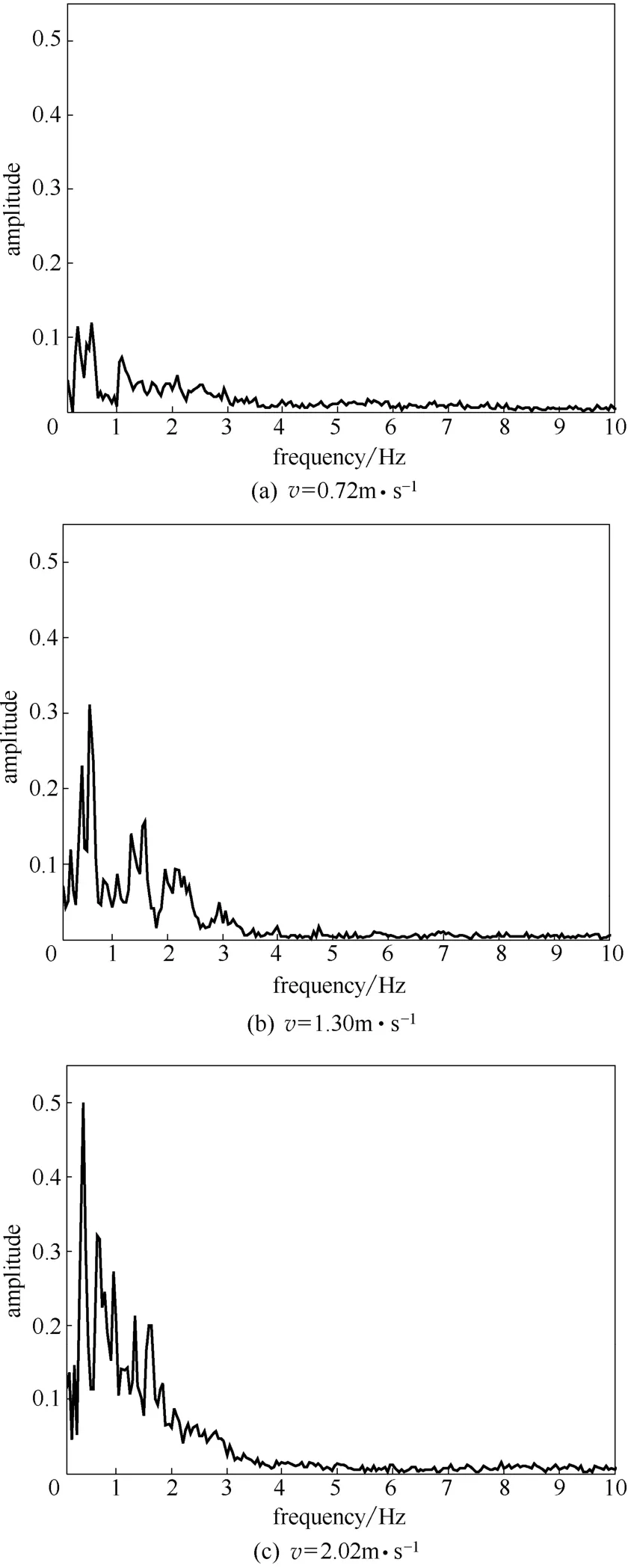
圖4 w=2%時不同氣速下壓差脈動信號的邊際譜Fig.4 Marginal spectrum of pressure fluctuation signal under different gas velocity when w=2%

圖4是生物質質量分數為2%，氣速分別在0.72、1.30 和2.02 m·s-1下的壓差脈動信號的邊 際譜。邊際譜可以真實地反映出壓差脈動信號頻率成分的真實情況，從圖中可以很清楚地發現3 幅圖呈現出一定的規律，壓差脈動信號的能量主要集中在0～4 Hz 的低頻部分，這與文獻[9]提出的觀點是一致的，此時幅值較大，可以認為0～4 Hz 為壓差脈動信號的主頻率區。而4～10 Hz 幅值較小，幾乎為零，此段頻率可以認為是干擾信號的頻率。從圖4(a)到圖4(c)，氣速逐漸增加，壓差脈動信號的能量越向低頻部分集中，而且低頻部分的能量也隨氣速增加逐漸增大，圖中表現為低頻部分幅值的不斷增大。這主要是因為流化床內氣泡是決定流動狀態的關鍵性因素，氣速的變化會改變氣泡原來的形狀、尺寸和運動規律。隨著氣速的增加，流化床內壓差逐漸變大，氣泡尺寸也跟著變大，氣泡的聚并、長大、上升、破裂所需要的時間越來越短，氣泡的周期性運動更加頻繁、劇烈，從而導致低頻部分幅值越來越大。

3.3 壓差脈動信號的能量分析

3.3.1 不同氣速下壓差脈動信號的能量分析 表2的數據表示生物質質量分數為2%時不同氣速下各階IMF 能量以及高中低頻能量百分比的分布情況。圖5為生物質質量分數為2%時高、中、低頻段能量隨氣速變化的曲線。

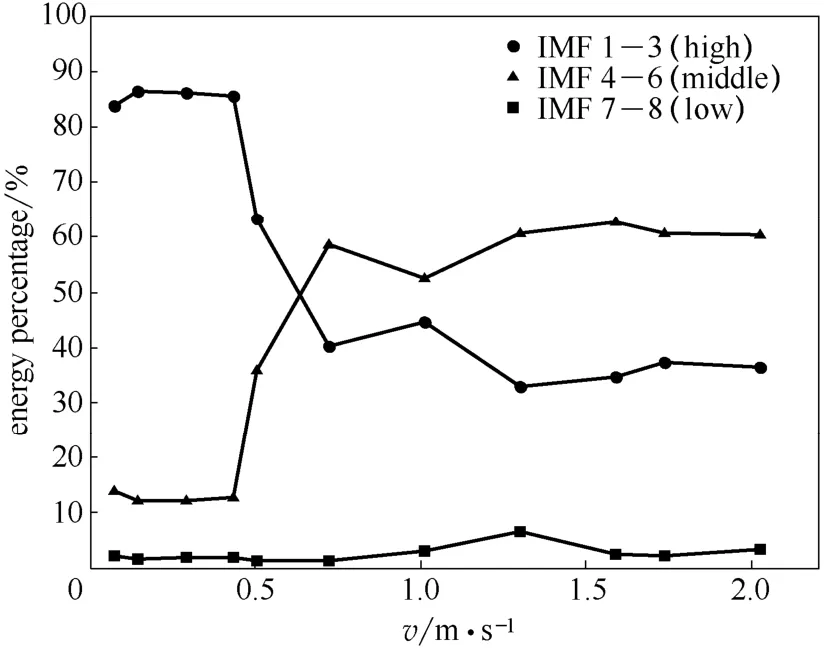
圖5 w=2%時高、中、低頻段能量隨氣速變化的曲線Fig.5 Curve of high,middle,low frequency energy under different gas velocity

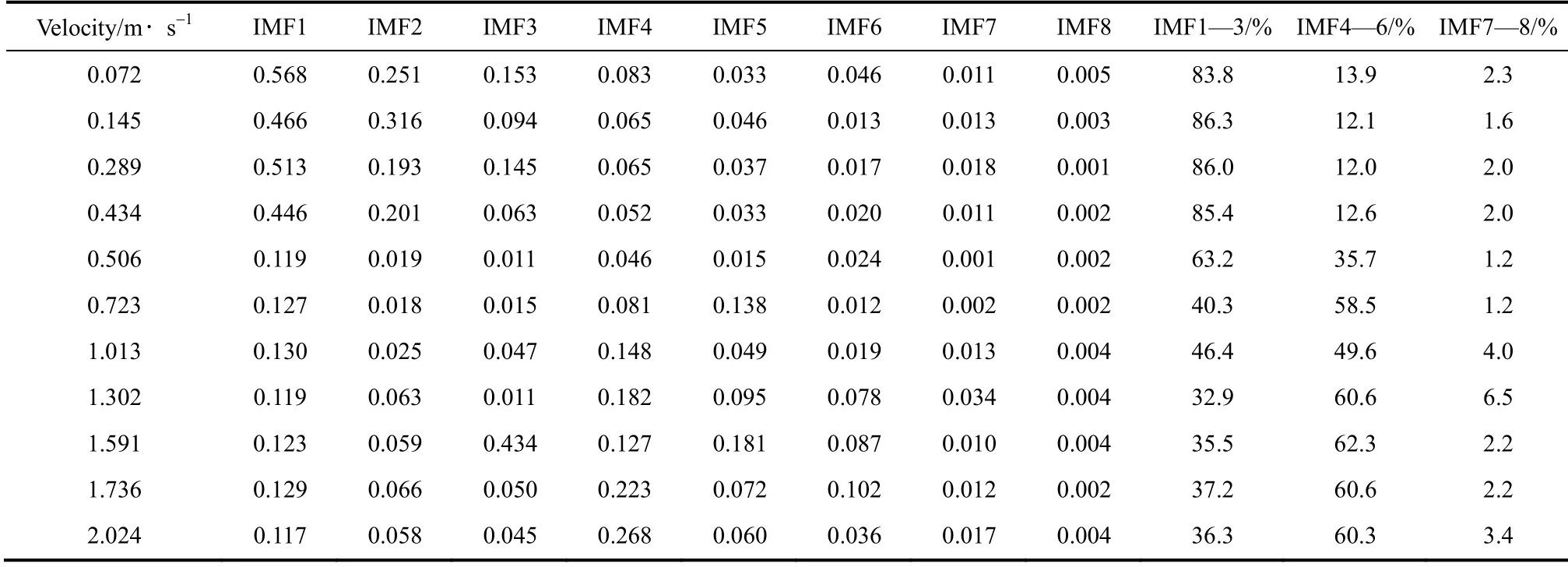
表2 w=2%時不同氣速下的IMF 均方值（能量）Table 2 Mean square values of IMF at different gas velocities when w=2%

圖6 v=1.01 m·s-1 時不同木桿質量分數的石英砂木桿雙組分顆粒流動狀態Fig.6 Two-component particle flow status of different biomass percentage at v=1.01 m·s-1

從表2和圖5可以發現，隨氣速的增加能量的集中區逐漸從高頻段向中頻段轉移，低頻段能量基本不變。當氣速較低（小于0.45 m·s-1）時，高頻段能量最高，達到86.3%。隨著氣速逐漸增加（0.45～1.3 m·s-1），高頻段能量快速下降，從 86.3%下降到32.9%；中頻段能量快速增加，從12.0%增加到62.3%。當氣速繼續增加時，高、中頻段能 量基本保持不變。高、中頻段能量的轉移是從臨界流化風速為v=0.45 m·s-1開始的，此時流化床內床料開始流態化，流化床逐漸進入鼓泡流化狀態，床內開始有氣泡產生，氣泡行為引起床料粒子運動低頻調制是造成這一能量轉移的主要原因，同時也進一步證明流化床內氣泡的運動是使氣固兩相流系統進入非線性、非平衡狀態的關鍵所在[8]。在氣速v≥1.30 m·s-1時，流化床內顆粒湍動均勻，氣泡具有一定的運動規律，此時高、中、低頻段能量不隨氣速的改變而改變。

3.3.2 不同生物質質量分數下壓差脈動信號的能量分析 如圖6所示，當氣速為1.01 m·s-1時流化床處于典型的鼓泡流化狀態，此時流化床內氣泡體積較大且氣固分界面明顯。在對氣固流化床研究中，這種工作狀態經常被視為研究對象。選取木桿質量分數分別為2%、4%、6%和8%的石英砂和木桿雙組分顆粒作為床料（混合均勻）。

圖6為木桿質量分數分別為2%、4%、6%和8%的雙組分顆粒混合流動狀態圖。圖6中(a)～(d)均描述木桿和石英砂顆粒在一個較短周期（1～1.5 s）內完成的流動狀態，每幅圖從左到右依次表示為流動起始狀態、過程狀態、結束狀態、進入下一個周期流動狀態。從圖中可以看出氣泡在流化床內開始形成，然后到慢慢長大，最后在氣固分界面破裂的整個過程。當生物質質量分數為2%、4%、6%時，流化床內大氣泡的邊界輪廓相對比較清晰，大致呈橢圓狀。當生物質質量分數為8%時，氣泡的邊界變得彎彎曲曲，小氣泡開始出現，此時床內不再是整個大氣泡在運動。這主要是因為，隨著生物質質量的增加以及生物質在密度、形狀、體積方面與石英砂存在較大的差異，生物質在被氣泡抬升后回落的過程中會破壞大氣泡的運動，使得大氣泡分裂成更小的氣泡。另外，從圖中可以看出，當生物質質量分數為2%、4%時，流化床內生物質與石英砂混合良好；當生物質質量分數為6%、8%時，流化床內出現分層現象，而且生物質量越多分層現象越明顯，如圖6(d)所示，有較多的生物質顆粒位于床料頂部。這主要是因為，生物質量增多，生物質顆粒之間開始抱團，而且氣泡在上升的過程中向四周排擠周圍的顆粒，生物質與石英砂相比密度較小，容易受到氣泡的排擠，氣泡周期性的上升運動將生物質顆粒排擠到床料頂部。

表3的數據表示氣速為1.01 m·s-1時不同生物質質量分數所對應的各階IMF 能量以及高、中、低頻能量百分比的分布情況。在氣速一定的情況下，生物質質量分數的改變會引起流化床內氣泡運動狀態改變，這也會帶來壓差脈動信號各階IMF 能量分布的變化。從表3可以發現，隨著生物質質量分數的增大，高頻段能量百分比逐漸增大，中頻段能量百分比逐漸減小，低頻段能量百分比較小且基本保持不變。這主要是因為，生物質顆粒增多必然會增大生物質對氣泡的擾動，在生物質顆粒下落的過程中會影響氣泡的聚并和長大，部分生物質顆粒穿過大氣泡的中心，干擾氣泡原來的運動路徑，將大氣泡破壞成小尺寸氣泡，導致氣泡頻率相對增加，從而引起高頻能量百分比的增加。正如圖6(d)所示，流化床內小氣泡數目明顯多于圖6(a)～(c)中的數目，這也導致了從w=6%時高頻段能量百分比50.5%快速增加到w=8%時高頻段能量百分比60.2%。

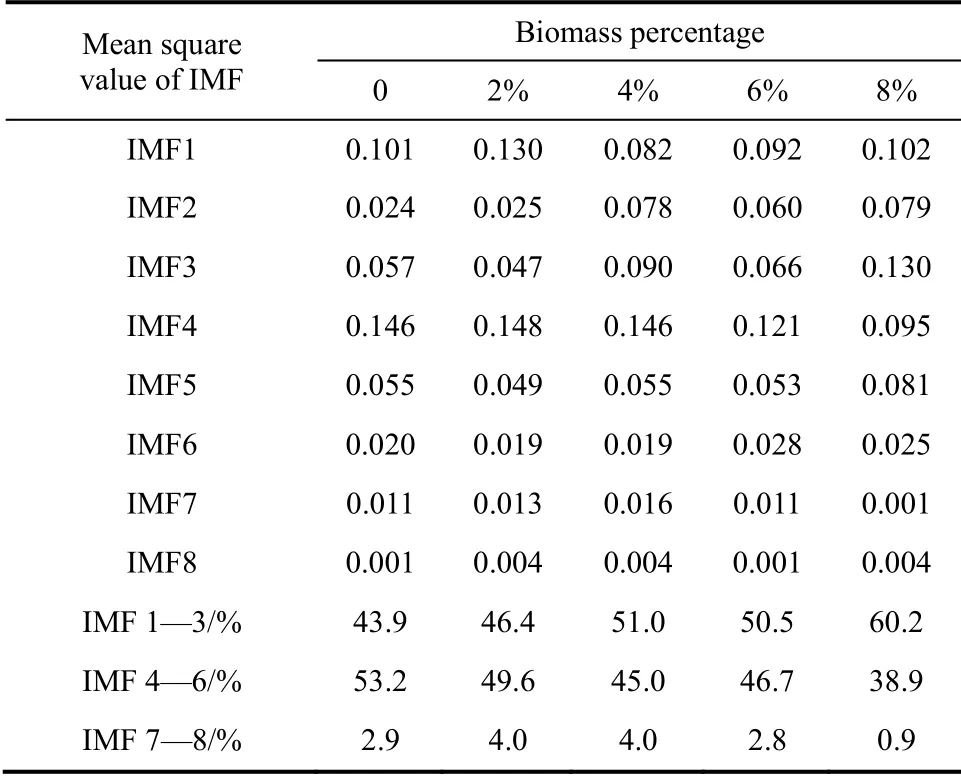
表3 氣速為1.01 m·s-1 的不同木桿質量分數的 IMF 均方值（能量）Table 3 Mean square values of IMF in different percentages of wooden pole at gas velocity v=1.01 m·s-1

對不同氣速時不同生物質質量分數下生物質與石英砂雙組分顆粒壓差脈動信號進行能量分析，能夠提取出一定的規律，為今后進一步研究流化床內雙組分顆粒流動提供一定的理論依據。

4 結 論

（1）采用HHT 法對不同氣速下流化床內生物質質量分數為2%的雙組分顆粒的壓差脈動信號進行邊際譜分析，得出壓差脈動信號頻率主要集中在0～4 Hz 低頻段，隨氣速增加壓差脈動信號頻率越向低頻段集中的結論。

（2）在生物質質量分數為2%的情況下對不同氣速下壓差脈動信號進行能量分析，發現在氣速小于臨界流化風速（v=0.45 m·s-1）時高頻段（IMF 1～3）能量百分比基本保持在85%左右；在氣速大于臨界流化風速流（v=0.45 m·s-1）時開始下降，逐漸向中頻段（IMF 4～6）轉移；在氣速v≥1.30 m·s-1時，高、中、低頻段能量不再隨氣速改變而改變。

（3）在氣速v=1.01 m·s-1情況下對不同生物質質量分數下壓差脈動信號進行能量分析，發現隨著生物質質量分數的增加，高頻段能量百分比逐漸增大，中頻段能量百分比逐漸減小，低頻段能量百分比基本保持不變。

符 號 說 明

HHT——Hilbert-Huang 變換

EMD——經驗模態分解

IMF——內稟模態函數

t——時間，s

v——表觀氣速，m·s-1

w——生物質質量分數，%

[1]Zhao Fengzhan (趙鳳展),Yang Rengang (楊仁剛).Voltage sag disturbance detection based on short time Fourier transform [J].Proceedings of CSEE(中國電機工程學報),2007,27 (10):28-34

[2]Luo Zhonghui (羅忠輝),Xue Xiaoning (薛曉寧),Wang Xiaozhen (王筱珍),et al.Study on the method of incipient motor bearing fault diagnosis based on wavelet transform and EMD [J].Proceedings ofCSEE(中國電機工程學報),2005,25 (14):125-129

[3]Sun Bin (孫斌),Zhou Yunlong (周云龍),Wang Qiang (王強).Differential pressure fluctuation analysis of gas-liquid two-phase intermittent flow using the wigner distribution [J].Chinese Journal of Scientific Instrument(儀器儀表學報),2005,26 (8):87-89

[4]Huang Hai (黃海),Huang Yilun (黃軼倫),Zhang Weidong (張衛東).Pressure fluctuations analysis of gas-solid fluidized bed using the wigner distribution [J].Journal of Chemical Industry and Engineering(China) (化工學報) ,1999,50 (4):477-482

[5]Wang Chunhua (王春華),Zhong Zhaoping (仲兆平),Li Rui (李睿),et al.Recurrence plots analysis of pressure fluctuation in gas-solids fluidized bed [J].CIESC Journal(化工學報) ,2010,61 (3):557-564

[6]Huang Bei (黃蓓),Chen Bochuan (陳伯川),Huang Yilun (黃軼倫).Analysis of pressure fluctuation in fluidized bed through algorithm complexity in various scales [J].Journal of Chemical Industry and Engineering(China) (化工學報),2002,53 (12):1270-1275

[7]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for non-linear and on-stationary time series analysis [J].Proceedings of Royal Society of London,Series A,1998,454:903-995

[8]Wang Xiaoping(王曉萍).The Hilbert-Huang transform and flow regimes identification for pressure fluctuation of gas-solid fluidized beds [J].Journal of Chemical Engineering of Chinese Universities(高校化學工程學報),2005,19 (4) :474-479

[9]Huang Hai (黃海),Huang Yilun (黃軼倫).Pressure-fluctuation analysis of gas-sold fluidized beds using Hilbert-Huang transform [J].Journal of Chemical Industry and Engineering(China) (化工學報) ,2004,55 (9):1441-1447

[10]Zhou Yunlong (周云龍),Wang Qiang (王強),Sun Bin (孫斌),Zhang Yonggang (張永剛).Applied study of Hilbert-Huang transform and Elman neural network on flow regime identification for gas liquid two-phase flow [J].Proceedings of CSEE(中國電機工程學報),2007,27 (11):50-56

[11]Wang Chunhua,Zhong Zhaoping,Li Rui.Flow regime recognition in the spouted bed based on Hilbert-Huang [J].Korean J.Chem.Eng.,2011,28 (1),308-313

[12]Ding Hao,Huang Zhiyao,Song Zhihuan,Yan Yong.Hilbert-Huang transform based signal analysis for the characterization of gas-liquid two-phase flow [J].Flow Measurement and Instrumentation,2006,18 (2007):37-46

[13]Lu Peng,Han Dong,Jiang Ruixue,Chen Xiaoping,Zhang Guichen.Experimental study on flow patterns of high-pressure gas-solid flow and Hilbert-Huang transform based analysis [J].Experimental Thermal and Fluid Science,2013,51:174-182

[14]Rai V K,Mohanty A R.Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform [J].Mechanical Systems and Signal Processing,2007,21:2607-2615

[15]Or-ampai Jaiboon,Benjapon Chalermsinsuwan,Lursuang Mekasut,Pornpote Piumsomboon.Effect of flow pattern on power spectral density of pressure fluctuation in various fluidization regime [J].Powder Technology,2013,233:215-226

[16]Qin Y,Qin S R,Mao Y F.Research on iterated Hilbert transform and its application in mechanical fault diagnosis [J].Mechanical Systems and Signal Processing,2008,22 (8):1967-1980

[17]Shen P C,Kang Y,Wang C C,et al.Study on the affection of gear fault diagnosis bases on HHT by noises [J].Advances in Intelligent and Soft Computing,2009,62:87-96

[18]Liu Qiang (劉強),Zhou Ruizhong (周瑞忠),Liu Yuhang (劉宇航).Computation and analysis of seismic response and energy based on Hilbert-Huang transform [J].Journal of Wuhan University:Engineering(武漢大學學報:工學版),2009,42 (6):780-784

[19]Liu Shangbao (劉雙寶),Lü Chao (呂超),Yu Jilai (于繼來),Wang Lixin (王立欣).Application of Hilbert-Huang transform in pattern recognition for partial discharge of transformers [J].Proceedings of CSEE(中國電機工程學報),2008,28 (31):114-119

[20]Wang Xiaoyi (王肖祎),Zhong Zhaoping (仲兆平),Wang Chunhua (王春華).Chaotic recurrence analysis of two-component flow of mixed biomass particles and quartz sands in fluidized-bed [J].CIESCJournal(化工學報),2014,65 (3):813-819

[21]Zhong Youming (鐘佑明),Qin Shuren (秦樹人),Tang Baoping (湯寶平).The theory research of Hilbert-Huang transform [J].Journal of Vibration and Shock(振動與沖擊),2002,21 (4):13-17

[22]Yang Jianwen (楊建文),Jia Minping (賈民平).Study on processing method and analysis of end problem of Hilbert-Huang spectrum [J].Journal of Vibration Engineering(振動工程學報),2006,19 (2):283-288