巧妙搭“橋” 化動為靜——關于2013年泉州市中考數學試題解答的商榷

◎福建省南安市金光中學 方明華

巧妙搭“橋” 化動為靜
——關于2013年泉州市中考數學試題解答的商榷

◎福建省南安市金光中學 方明華

動態幾何題題型新穎，既考查了多個知識點，又考查了多種運用數學思想的能力，試題綜合性強.這就要求考生能夠嚴密細致地觀察問題，理清解答思路，采用構造法“搭橋引路，化動為靜”，充分利用已知的條件去推導問題和解決問題。

中考數學；動態幾何題；構造法；答案修正

動態幾何題題型新穎，在考查中往往能呈現出較高的區分度，因此成為中考命題中的重要題型，也受到中學師生的高度關注.這種題型所考查的往往是多個知識點，同時考查多種運用數學思想的能力，涉及的知識面廣，試題綜合性強.所以在解答這一類的動態幾何題時，要求考生能夠嚴密細致地從多個角度觀察問題，充分利用已知的條件分析問題，十分嚴謹地推導和解決問題，才能正確完整地寫出答案.現以2013年泉州市中考數學試題的第25題為例，談談這個方面的一些見解.

一、理清思路，周密解答

（1）求∠ABC的大小；

（2）求點 P 的坐標，使∠APO=30°；

（3）在坐標平面內，平移直線BC，試探索：當BC在不同位置時，使∠APO=30°的點P的個數是否保持不變？若不變，指出點P的個數有幾個？若改變，指出點P的個數情況，并簡要說明理由．

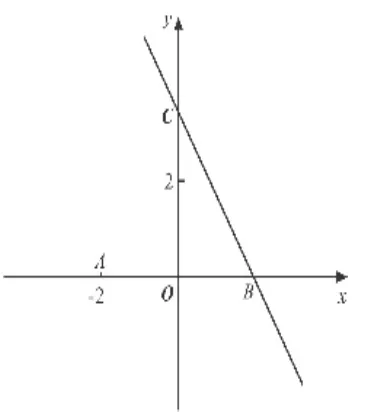
本題的命題立意是，以平面坐標為依托，考查幾何、代數的相關知識點及數學方法的運用。其考查的知識與能力的范圍橫跨整個初中學段，知識覆蓋面寬，方法包容性強，拓展輻射作用大.據統計，考生在這一題的平均得分為5.6分，獲得10分以上高分的人數很少。如何在解題中做到深入細致地觀察問題與推導問題，從而正確完整地解答問題，以下是具體的分析解答步驟.

步驟一，第（1）小題求∠ABC大小.

本小題考查的是關于“方程與一次函數的關系”這一知識點的掌握運用情況，其解答思路是先觀察角的位置，在此基礎上運用三角形的方法解決問題，這里需要運用直角三角形或特殊三角形的方法.

連接 AC（如圖二示），由 A、B兩點的坐標可知，它們關于y軸對稱，由對稱性質得AC＝BC，再運用勾股定理求得AC＝BC＝4，由此判斷△ABC為等邊三角形，可得∠ABC=600，并為解答第（2）小題作鋪墊．

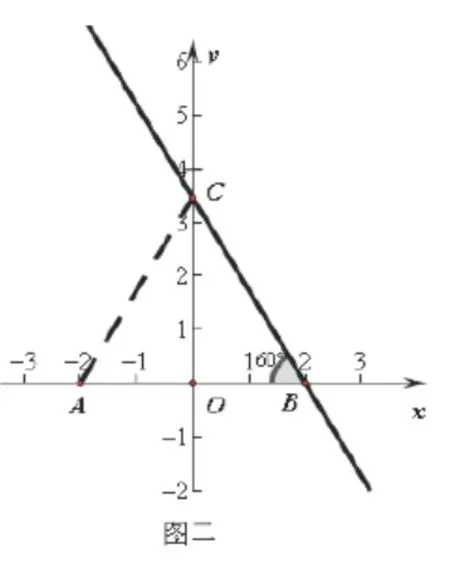
步驟二，第（2）小題求點P的坐標，條件使∠APO=300．

首先觀察∠AOC的度數，利用“在圓中，直徑所對圓周角為直角”這一知識點，得出A、O、C三點共圓，因此通過構造圓搭“橋”引路（如圖三示），得出弦AO所對圓心角為600，這就把解決本問題轉化為以AC為直徑的圓與直線BC的公共點問題，即直線與圓的位置關系，可以看到有兩個點符合題目規定的條件.

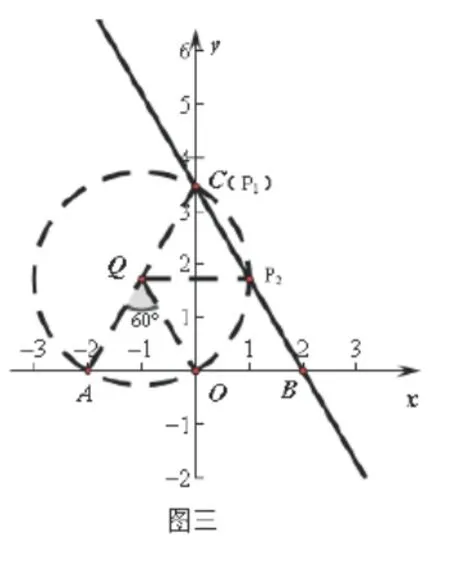
步驟三，對于第（3）小題，是動態幾何問題，主要是考查動手操作能力和探索、分析、解決問題的能力．

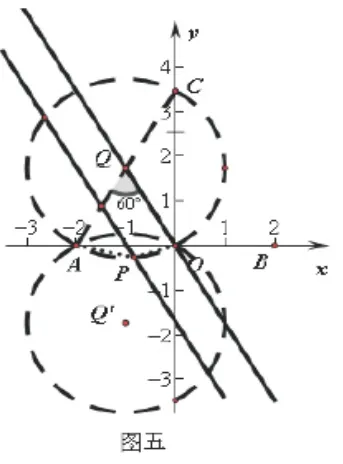
在動直線BC上尋找符合條件的點P，可在第（2）小題的基礎上進一步思考，300的圓周角所對弧為AO，該弧所對的圓心角為600．因此，同樣可以通過以AO為弦構造圓進行搭橋，根據對稱性原理可知，這樣的圓有兩個（如圖四示），根據“同弧所對圓心角是圓周角的2倍”這一原理得出，符合條件的點P實際上是直線BC與兩圓的公共點，這也把問題轉化為解決直線與圓的位置關系問題。再通過動手操作，運動直線BC，進行分類討論，得出直線BC在不同位置時，點P的個數變化．不妨記兩圓為⊙Q，⊙Q′，點Q，Q′關于x軸對稱，點P的個數情況有四種情況，即有1個、2個、3個、4個.

這里，命題者提供本小題的參考答案中，有三處答案值得商榷，應加以修正.

第①處，如下列所示

第①處修正理由：假如點 在⊙Q，⊙Q′這兩個圓被軸截成的兩段劣弧中（如圖五示），則只能使∠APO=150°；假如點P與點A或點O重合時，則∠APO不存在.

所以答案應修正為：

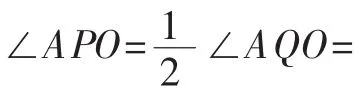
第②、③處，如下列所示：

數學試題參考答案及評分標準 第6頁（共8頁）

第②處的修正理由：當點P與點A或點O重合時，∠APO不存在，則使∠APO=30°的點P只有兩個．

所以答案應修正為：“直線BC過⊙Q與⊙Q′的一個交點，同時與兩圓都相交”的部分應屬于第2種類；

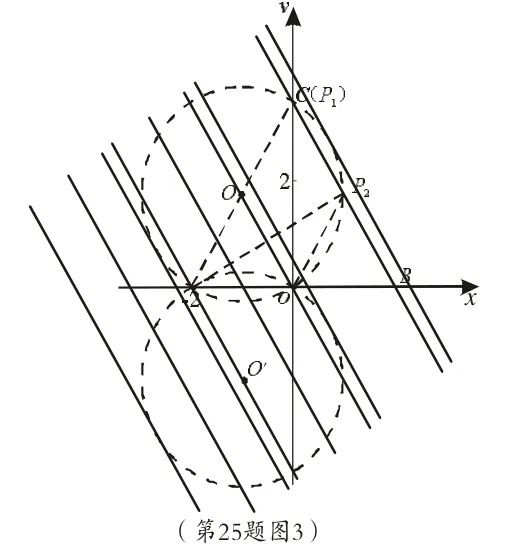
第③處的修正理由：當直線同時與⊙Q、⊙Q′都相交且不過兩圓交點時，將出現兩種情形：

一是當直線BC同時與兩圓都相交且與弦AO不相交時，則點P有4個；

二是當直線BC與兩圓都相交且與弦AO相交，且不過兩圓的交點時，從理論上講應有四個交點，其中與劣弧AO相交的兩個點P，使得∠APO=150°，不符合題意，所以點P的個數也只有2個．

所以答案應修正為：

“Ⅳ）有4個：直線BC同時與兩圓都相交且與弦AO不相交”；

第二種情形應屬于第2類．

通過以上的分析可以看出，本題在參考答案的制作過程中，由于忽略了直線BC與圓的公共點P所形成的角不存在，或在劣弧AO上所形成的∠APO=150°不合題意，導致答案表述不嚴密.

二、搭橋引路，化動為靜

依據辯證法原理，動與靜存在著相互對立又相互依存的關系，動依賴靜而存在.本題是一道典型的幾何動態綜合問題，一方面，點在直線上運動；另一方面，直線又在平面上平移.運用構造法是解決本題問題的關鍵，即根據題設條件和問題的特殊性，構造出一些新的數學形式，搭橋引路，化動態為靜態，并借助它們認識并解決原先的問題.構造法具有多種形式，應用范圍廣，具有靈活性與技巧性，是重要的數學解題方法之一.本題在解題過程中所運用的是構造圖形法，通過構造圓搭起動與靜的“橋梁“，即以∠APO=30°為前提，構造以AO為弦的圓，目的是通過構造圓這一圖形直觀地揭示已知與未知的關系，確定論證點P的位置，使證題的思路豁然開朗，就如“山重水復疑無路，柳暗花明又一村”.

本題所體現的考查目標，給了中學數學教學重要啟示：教師在課堂教學中，應著力培養學生觀察能力，能充分利用已知條件進行嚴謹推導，從中發現條件與結論的聯系，為問題的解決創造條件.在解題教學中，應選取具有代表性的好問題，充分挖掘題目所蘊含的思想價值，給予學生自主學習與合作探究的時空，引導學生審清題意，理清思路，完整解答，通過典型問題這一把“鑰匙”開一類“鎖”，使學生“做一題、通一類、會一片”，不斷提高學生的動態思維、創新思維和想象能力.

（責任編輯：王欽敏）