巧設問題情境

許玲麗

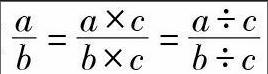
筆者在教學第十冊“分數的基本性質”一課時，通過認真閱讀分析教材，結合學生的思維能力和認知水平考慮，認為依照課本上編排的程序進行教學，會在一定程度上限制學生創造性思維的發展。于是，筆者大膽改進教學設計方案，直接創設問題情境，導入新知。首先出示問題：你會用分數表示下圖中陰影部分的大小嗎？

學生在已有“分數的意義”這一認知基礎上，首先想到的答案是[48]，再通過深入觀察思考，又有學生說出“[24]、[12]”，也可以表示圖中陰影部分的大小。一些學生頓生疑問，產生認知沖突，內心處于一種不平衡狀態，急切渴望再學習、再探究。

學生有了強烈的學習欲望，筆者又不失時機地為他們創造條件，讓他們按四人一組合作研究、自主探索。

學生在各自的小組中展開了熱烈的討論。有的學生認為，圖中正方形平均分成了8份，陰影部分占了這樣的4份，所以只有[48]這個答案正確。這些學生的思維還只停留在已有知識的層面上。有的學生認為三個分數表示的結果都正確，雖然圖中把正方形平均分成了8份，我們可以把圖中的每兩個小三角形看作一份，這樣就可以看作把正方形平均分成了4份，陰影部分占這樣的2份。也可以把圖中每兩個正方形看作一份，這樣這個圖形就可以被看作平均分成了2份，陰影部分占這樣的l份，所以用[24]、[12]表示陰影部分也正確。這些學生的思維活動就更深入了一步，并且還動手畫出下列圖形進行展示：

學生們爭論不休的時刻，也正是他們在積極參與整個學習活動，經歷著數學知識的探索過程的時刻。在這一討論過程中，學生們之間的能力差別和潛在的創造力都展現了出來。他們在相互啟發下，對問題有了新的答案。有的學生發現，[816]、[1632]也可以表示圖中陰影部分的大小，他們邊說明邊折紙展示（如下圖）來驗證自己答案的正確性。

通過熱烈爭論，學生不僅有了新發現，思維品質也得到不斷升華。有的學生大膽猜想：答案有無數個。

猜想是一種創造性的直覺思維方式，是關于數學規律的聯想和設想。教學中，創設這樣的問題情境，鼓勵學生大膽猜想，對學生創造性思維的發展無疑會起到一定的促進作用。

學生很快說出這一列分數大小相等，分子、分母都在不斷變化，并正確地找出了分子、分母變化的規律。如下面板書：

在學生用簡潔的語言概括出分數的分子、分母變化的規律后，緊接著，筆者把學生引入“驗證”階段，通過互動，用實例驗證了分子、分母變化的規律，最后學生用具有代表性的例證[ab]=[a×cb×c]=[a÷cb÷c]（b、c都不為0）構建起“商不變性質”與“分數的基本性質”之間的內在聯系，并概括出“分數的基本性質”這一重要結論。

通過這一課的教學，筆者深刻地認識到，在課堂教學中，應該完全以學生為主體，教師啟發、引導都要適時，要巧妙創設問題情境，讓學生去探索、總結，積極開展思維活動，這樣我們才能真正把素質教育落實處。

（作者單位：荊門市教育科學研究所）