高中數學中含參問題的解題初探

喻金武

(福建省莆田華僑中學)

含參問題一般是把不等式、函數、三角、幾何等內容有機地結合在一起，綜合性強、解法靈活等特點成為近幾年高考及高中數學聯賽的熱點之一.含參問題的解題方法是多樣的，涉及各種數學思想和方法，下面通過例子來展示各種解題方法.

一、變量易位

變量易位是含參問題的一種重要解題策略.含參問題，一般含有兩個或多個變元，我們在解題過程中可視其中一個為主元，其余都看作參數，可將多元問題化為一元問題，常常可以降低思維難度.變量易位可分為兩種：

1.主次元互換

一般的，把已知范圍的變量看作自變量，另一個看作常量.

例1.對于0≤p≤4的一切實數，不等式x2+px>4x+p-3恒成立，求x的取值范圍.

分析：解決這個問題需要應用二次函數以及二次方程實數根分布原理，這是比較復雜的.若把x與p互換一下角色，即將p視為變量，x為常量，則上述問題可轉化為關于p的一次函數在［0，4］內大于0恒成立的問題.

解：設f(p)=(x-1)p+x2-4x+3

當x=1時，不滿足題意，

當0≤p≤4時，f(p)>0恒成立，只要f(0)>0且f(4)>0

即x2-4x+3>0且x2-1>0解得x>3或x<-1.

2.多元問題確定主元

例2.對任意a∈［-1，1］，函數f(x)=x2+(a-4)x+4-2a的值總大于0，求x的取值范圍.

解析：f(x)的表達式是以x為主元的，若按此思路做下去，就會被騙了，若以a為主元，則發現g(a)=f(x)=(x-2)a+x2-4x+4是以a為自變量的一次函數.只要同時滿足 g(1)>0 及 g(-1)>0 即可，而g(1)=(x-2)+x2-4x+4=x2-3x+2>0，g(-1)=(x-2)(-1)+x2-4x+4=x2-5x+6>0即x>3或 x<1.

二、分段討論

合理分段討論是處理含參問題的基本思路，含參問題的字母取值范圍的求法通常需要用分段討論的方法來解決.

1.異元分類

解：令log3x=t，則原方程可化為

故原不等式的解集為：當 k∈(-1，0)∪(1，+∝)時3k)，當 k∈(-1，1)時，x∈覫

2.同元分類

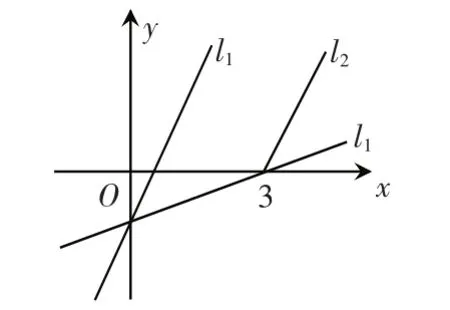
例4.設log(x2x+1)

解：根據對數函數的單調性對x進行分類：

當03x>1解得當x>1時，可得x>1且2x2+1<3x<1，解得x∈覫，

3.轉變視角

利用等價變形、函數奇偶性及公式的合理選用，變換視角去解題.

例5.設(fx)是偶函數，x∈［-2，2］，且x∈［0，2］時，(fx)為減函數，解不等式 (f1-a)<(fa).

4.數形結合

有些問題，僅限于數方面的考慮，在解決問題時，過程較為繁瑣，若既能分析數式特征，又能揭示幾何意義，巧妙結合，則更有利于問題的解決.

例 6.設關于 x的方程 lg(ax-1)-lg(x-3)=1 有解，求實數 a 的取值范圍.

解：原方程可化為：lg(ax-1)=lg10(x-3)從而 ax-1=10(x-3)(x>3)

設 y1=ax-1，y2=10(x-3)(x>3)，其圖象分別為 l1，l2，

總之，對于含參問題，因其覆蓋的知識點多，方法多，應充分運用到各種思維策略和方法.

［1］蘇龍.談主元思想對參數問題的解題幫助［J］.福建中學數學，2008(11)：35-37.

［2］曾安雄.避免分類討論簡化含參問題［J］.解題技法，2006(3)：24-27.