“再造”數(shù)學經(jīng)驗 提升數(shù)學能力

張秀華

[摘 要] 增加學生的數(shù)學活動經(jīng)驗，首先要注重數(shù)學基礎知識的獲得，然后從數(shù)學活動中引導學生提升自主學習能力. 雖然在現(xiàn)在的數(shù)學教學課堂中，教師不斷重視數(shù)學活動的重要性，但教師還需要掌握更多的技巧，才能達到數(shù)學活動質(zhì)量的提高，讓學生積累更多的數(shù)學活動經(jīng)驗.

[關鍵詞] 數(shù)學活動經(jīng)驗；生活；個性；替代

數(shù)學經(jīng)驗是數(shù)學的感性認識，是學生在數(shù)學活動中積累的能力. 新的課程標準將學生的“數(shù)學經(jīng)驗”提升到非常重要的位置，如何在教學中提升學生的“數(shù)學經(jīng)驗”，提升數(shù)學能力，筆者作了大膽探索.

聯(lián)系生活中的數(shù)學，積累數(shù)學

活動經(jīng)驗

在教學中，我們認識到數(shù)學活動經(jīng)驗是建立在生活的基礎之上，所以要讓學生在日常生活中掌握數(shù)學經(jīng)驗，并認識到數(shù)學滲透在生活的各個方面. 學生只有將生活中的數(shù)學現(xiàn)象與課本上的數(shù)學知識相結(jié)合，才能將抽象的數(shù)學轉(zhuǎn)為“有生命”的數(shù)學. 在教學中，教師要善于調(diào)動學生的生活經(jīng)驗，這樣才能既提高學生的學習興趣，又引導學生主動思考.

例如，在“認數(shù)”的教學中，教師出示美麗的小山村（板書“1”），讓學生觀察一條狗、一棵蘋果樹、一條小河、一條船、一間房子、一個小朋友等，這些生活中的景物數(shù)量可以用“1”來表示，發(fā)現(xiàn)數(shù)量的表示形式. 所以，這里獲得的經(jīng)驗與所有物體的性質(zhì)沒有關系，完全可用數(shù)學符號“1”來代替，這就是邏輯數(shù)學經(jīng)驗的獲得，一個依賴于外界事物而又超越其具體形態(tài)的抽象過程.

數(shù)學教學的材料越貼近學生的生活，就越能激發(fā)學生的主動思考，學生在學習過程中就更加積極. 孩子在入學之前雖然也有認識數(shù)字的概念，但對數(shù)字的認識還是抽象的，大多不能用數(shù)字進行數(shù)數(shù). 教師在教學中，可以把抽象的數(shù)字與兒童的周圍生活環(huán)境相結(jié)合，可以先從兒童感興趣的糖果開始，進一步數(shù)出自己身邊可以用“1”表示的物體，引導兒童探索數(shù)學的奇妙，獲得更多的活動經(jīng)驗. 同時，也可以鼓勵家長在平時生活中吸引孩子們自然地進入知識經(jīng)驗遷移，興趣盎然地去數(shù)數(shù)，打開數(shù)學思考的大門. 因此，數(shù)學教師在教學中，要把數(shù)學內(nèi)容和兒童的生活聯(lián)系在一起，但這個聯(lián)系必須在兒童的認知范圍內(nèi)，還應考慮到兒童的理解能力，用充滿童趣和歡快的內(nèi)容引起兒童的興趣.

明確數(shù)學活動目的，總結(jié)數(shù)學

活動經(jīng)驗

任何一項活動，在不同的理解和引導下都會形成不同的結(jié)果與經(jīng)驗，數(shù)學活動也是如此. 如果教師進行不當?shù)囊龑В瑫o學生造成困惑，這反而會給學生的活動經(jīng)驗形成負面影響. 因此，在開展數(shù)學活動時，教師應提出數(shù)學活動目的，讓每一個學生明確這項數(shù)學活動的目的，在確定的學習目標下進行活動，達到有效地提高數(shù)學活動能力、積累數(shù)學活動經(jīng)驗的效果.

例如，在一堂數(shù)學公開課“大樹有多高”的課堂上，某位教師在課前布置任務，即采取小組活動的方式，去學校的操場進行測量，并記錄下數(shù)據(jù). 課堂上，該教師首先把鉛筆的實際高度和影長、數(shù)學書的實際高度和影長、某位同學的實際高度和影長等數(shù)據(jù)都一一呈現(xiàn)在黑板上，然后組織學生進行小組討論，要求學生找到規(guī)律. 但很多同學都會發(fā)現(xiàn)自己測量的數(shù)據(jù)與老師在多媒體上展示的數(shù)據(jù)有很大的差別. 當大家都在爭執(zhí)誰對誰錯時，這個過程已經(jīng)浪費了很多時間，也做了許多無用功，最終，沒有一個小組得出準確結(jié)果.

在這堂課中，學生的測量結(jié)果和準確數(shù)據(jù)不一致的原因是實驗測量的誤差，而這名教師在上課前并未認識到這一點，因此沒有達到預期的教學效果. 如果教師在課前就明確告訴學生實際測量存在誤差，并要求小組在課前測量后，合作計算準確的大樹高度和影子長度的比值，這樣就能大大節(jié)約課堂時間. 同時，也可以讓學生在課前的數(shù)學活動中自己理解誤差的概念，而不是在短暫的課堂上難以理解甚至完全沒有理解. 充分的課前數(shù)學活動也給學生創(chuàng)造了分析活動數(shù)據(jù)、體會活動經(jīng)驗的很好機會.

做好活動準備，從經(jīng)歷走向經(jīng)驗

簡單的數(shù)學活動并不一定能讓學生獲得能力，只能稱作數(shù)學經(jīng)歷，只有明確、合適的數(shù)學活動才能獲得數(shù)學經(jīng)驗，讓學生有自己的數(shù)學活動理解，構(gòu)成自己的活動體系. 作為教師，應設計好數(shù)學活動過程，準確地引導學生完成數(shù)學活動，獲得必要的數(shù)學活動經(jīng)驗.

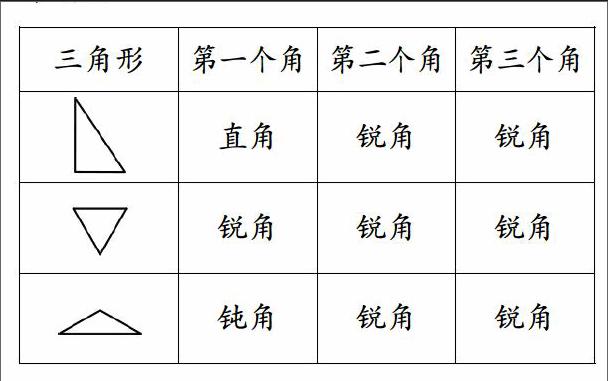
例如，教學“三角形分類”一課時，教師設計了以下幾個活動.

活動一：請畫出一個三角形，并標上角1，2，3，然后量一量哪些角是銳角、直角、鈍角. 接著請學生回答.

活動二：請再畫出幾個三角形，并且要和剛剛的三角形不相同，至少畫出三個.

最后，請學生板演，然后完成導學案：

活動三：教師板演，請同學回答能夠得到哪些關于三角形的知識.

數(shù)學學習活動是一項注重學生理解和體驗的活動. 在教師的教學中，要創(chuàng)造一個學生自主探索發(fā)現(xiàn)的過程，讓學生積極地投入到數(shù)學活動中，主動地發(fā)現(xiàn)數(shù)學規(guī)律，加深自己的理解，一步一步地得到活動結(jié)果. 這就要求教師在設計活動過程時，應明確每個過程的目的，要求每個環(huán)節(jié)都達到獲得活動技能、數(shù)學知識的效果.

另外，要注意，有些教師會因為理解不透，數(shù)學經(jīng)驗往往會變成數(shù)學經(jīng)歷. 例如，在一堂公開課上，一位教師通過小棒來認識三角形三條邊之間的關系時，并沒有理解“活動經(jīng)驗”的含義.

師：我現(xiàn)在有一根3厘米和一根5厘米長的小棒，現(xiàn)在老師想圍成一個三角形，你認為第三根小棒會多長？

學生開始猜測小棒的長度.

師：我現(xiàn)在有10根小棒，分別是1厘米、2厘米······一直到10厘米， 我請同學來擺一擺，哪些長度的小棒能與3厘米長和5厘米長的小棒圍成一個三角形. 請大家先在小組里交流，待會我請同學來講臺演示.

最后，學生回答完，教師給大家公布了合適的小棒長度.

在這個教學過程中，學生雖然參與了擺小棒的過程，但完全變成了活動經(jīng)歷. 學生根本不明白擺小棒的用意，也不知道這項數(shù)學活動的最終目的. 這位教師只是把數(shù)學活動簡單地理解為了動手操作，沒有意識到讓學生在這項數(shù)學活動中獲得數(shù)學活動經(jīng)驗. 所以，數(shù)學教學如果只是單純地動手操作，學生就會變成生產(chǎn)線上沒有思想的“操作工”，學生的思維就會被僵化，不能形成數(shù)學思想. 如果這名教師在這項數(shù)學活動中布置提升內(nèi)容，要求學生自己舉例能夠擺出三角形的三根小棒長度，或者要求學生總結(jié)原因，就會讓學生不但動手，也動腦. 因此，在數(shù)學課堂上，教師要清楚認識“數(shù)學經(jīng)驗”該如何培養(yǎng)，強調(diào)數(shù)學思維的形成，注重數(shù)學經(jīng)驗的獲得.

注重個性表達，提倡共享數(shù)學

經(jīng)驗

學生作為數(shù)學活動的主體，有著獨特的主觀性. 教師在數(shù)學活動中，不能將自己的觀點強加于學生，也不能抑制學生的個性發(fā)展. 每個學生都有自己的個性，這使得不同的學生在參與數(shù)學活動時有不同的問題解決方法，此時教師應該作為引導者. 在目前的教育目標下，數(shù)學教學必須面對全體學生，面對不同的學生，要區(qū)別對待.

首先，應創(chuàng)造輕松的教學氛圍，處理好師生關系以及學生之間的關系. 其次，在教學方式上，給每個學生表達自己觀點的機會，同時，我們提倡小組交流，這也能促進學生之間的關系，讓學生在學校過程中建立良好關系，共享數(shù)學學習經(jīng)驗. 最后，教師應關注有個性的學生，既不讓他們脫離群體，也能讓他們適時地展示自己的個性. 例如，在數(shù)學活動中，我們多采用小組的形式開展活動，但在小組活動的同時，也給每個學生表達自己觀點的機會. 還可以根據(jù)小組活動的不同，考慮個別學生的個性，分配不同的數(shù)學活動任務，讓學生表達自己的觀點，促進數(shù)學交流.

尋找“替代經(jīng)驗”，激活情感經(jīng)驗

目前，對于“活動經(jīng)驗”，有不同的理解. 很多人認為活動經(jīng)驗一定是親力親為才能有所獲得. 親歷雖然是數(shù)學活動的重要方式，但也有許多別的方法可以使學生間接得到活動經(jīng)驗. 因為，數(shù)學有著獨特的精密性、復雜性，很多數(shù)學活動是學生無法直接參與的. 這時，教師可以通過自己的演示，例如常見的多媒體演示和幾何畫板應用，可以使學生在視覺上得到信息，從而獲得經(jīng)驗，加深理解. 但教師的操作決定了學生是否能夠準確地獲得經(jīng)驗. 教師的活動經(jīng)驗要求教師能夠站在學生的角度，考慮到學生的理解力和接受力進行演示，從而使學生獲得“替代經(jīng)驗”.

學生只有經(jīng)歷豐富的數(shù)學活動，才能得到自己的數(shù)學感悟，形成自己的數(shù)學思維，獲得自己的數(shù)學活動經(jīng)驗，從而在今后的數(shù)學學習中，自主積累數(shù)學活動經(jīng)驗.endprint