“變教為學”看錯誤

賈小麗

“變教為學”的課堂中，學生的錯誤屢見不鮮。為了將學生出現的錯誤轉變為教學資源，就需要對造成學生發生錯誤的心理方面的原因有所了解。進而可以有效地診斷學生在學習中的困難，并進一步有針對性地幫助學生學習。個體心理異常復雜，可以概括為認知、情感、能力和人格。造成學生出現錯誤的原因也多種多樣，下面主要從“認知”方面的注意、記憶、思維和情感方面舉例說明。

一、注意的轉移能力差

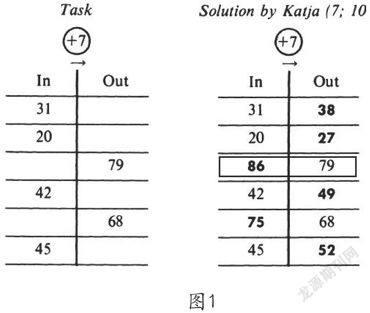
注意轉移是個體根據新的任務，主動地將注意從一個對象過渡到另一個對象上。小學生由于注意轉移能力較差，所以會出現許多錯誤。如在接近整十、整百數的加減法的練習題16+99、35+198、74+297中夾一道68+101，學生就會計算成68+101=68+100-1，原因是其注意力還停留在一個數加上一個小于整百的數，未能將其轉移到一個數加上一個大于整百的數，因此在計算68+101時加上了一個整百數，又減去一個數。給學生布置如圖1[1]的任務，輸入部分（in）加上7即為輸出部分（out），前兩道題31+7=38、20+7=27，第三道題學生依舊得出79+7=86，注意力還停留在加7上，未能將其過渡到減7，因而得到一個錯誤的結果。

圖1

在乘除法計算中由于學生注意未能及時轉移也會出現錯誤，如圖2案例中乘法口訣“四八三十二”最后的“二”被錯誤地當成下一步的進位數字了，這句話最后的發音是乘積的個位數字“二”，學生的注意力集中在“2”上，未能集中在“3”上，所以就不自覺地把數字“2”用到下面的計算中，在圖3案例中也是類似的錯誤。一個數的千分位上是6，十分位上是4，百位上是3，其余各位都是0，這個數是幾？學生的答案為0.436，錯誤的原因是前面為千分位、十分位，把隨后的百位也看成了百分位，所以認為百分位上是3。此外，在應用題中也存在這樣的問題，如圖4，學生在回答第二個問題時，錯誤地使用了第一個問題的答案，學生對“車上有多少人”的判斷還停留在第一個問題上，認為現在車上有57人，又上來9人，直接得出57+9=66。

圖2 ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖3

圖4

由注意的轉移能力差引起的錯誤和心理學中“perseveration”（持續重復某一動作或言語的行為）有著密切聯系，已經說出的成分或已經進行的行為會取代或干擾將要進行的行為，使將要進行的行為出現錯誤。美國學者Percival M.Symonds認為人們行為的特點“perseveration”，可以解釋許多錯誤，如24×8得到的結果為182，由于4×8=32，其中持續重復“2”這一聲音，取代了“3”，從而和2×8=16結合起來，得到16+2=18這樣錯誤的答案，[2]這和圖2的案例頗為相似。德國學者Pippig認為9×60=560，5×13=63，41+7=47這樣的錯誤也是由“perseveration”引起的。[3]

二、工作記憶的有限性

人的認知結構由工作記憶（working memory）和長時記憶（long-term memory）組成，長時記憶的容量幾乎是無限的，而工作記憶的容量是有限的。由于工作記憶的有限性，當學習內容對工作記憶要求越高，錯誤發生的可能性就越高。有關工作記憶與數學錯誤的早期研究來自Hitch的實驗，他發現如果解題者在心算時忘記了初始信息或中間步驟，結果就會產生計算錯誤。[4]因此，錯誤是由于與問題有關的信息在記憶中產生衰退造成的。

在列式計算“602-436=？”時，學生得出錯誤答案266，主要是因為學生不僅要考慮每個數位上的數對應相減，還要考慮借位。在被減數個位和十位連續兩次借位后，往往在百位上用6和4直接相減，從而得到結果為266。學生并不是不知道算法規則，而是由于在計算中因素考慮比較多，產生認知負荷超載，對工作記憶的要求高，因此使得錯誤產生;在加法中也會有類似的錯誤，如計算358+143的結果為401，學生只記得十位上加一，忘了百位上也要加一;在多位數乘法計算中，還會出現這樣的錯誤，如圖5學生在計算546乘8時，把個位數字6和十位數字4分別和8相乘后，忽視了百位數字5和8的計算;在學習除法豎式計算時，只顧及試商而未顧及觀察余數是否比除數小，從而造成商的位數增多。另外，在四則混合運算中，注意了括號內的運算順序，而不注意括號外的運算順序;在關于比較的應用題中有兩種類型，第一種類型為“甲有a個，乙比甲多（少）b個或乙是甲的c倍，問乙是多少”，第二種類型為“甲有a個，比乙多（少）b個或是乙的c倍，問乙是多少”。學生在解決第二種類型的題時會遇到困難，產生錯誤。如圖6，此題期望學生用加法“1.24+0.12=1.36”計算，可學生偏偏列出減法算式“1.24-0.12=1.12”。這一結果可以用工作記憶負荷來解釋，與第一種類型題相比，兒童必須對第二類型題中的關系陳述進行轉化，加重了工作記憶負荷，因而導致錯誤的發生。

圖6

法國克萊蒙費朗第二大學心理學教授Michel Fayol曾對簡單的應用問題進行研究發現：文本的不同組織方式將使學生成績產生顯著差異。例如，改變應用題的表達順序導致更多的錯誤和較低的成績，他認為特定的文本結構使問題解決者產生超負荷的工作記憶從而引起錯誤的增多。[5]此外，研究者Inez E.Berends對應用題有無插圖對學生成績的影響進行了研究，他認為兒童需要在插圖信息和文本信息之間進行注意轉換，整合插圖信息和文本信息也會造成工作記憶的負荷。[6]因此，有插圖的應用題對問題解決者可能會產生較高的認知負荷，影響學生問題解答的準確率，當然這只是可能并非一定。

三、思維定勢的消極影響

思維定勢（mind-set）就是按照積累的思維活動經驗和已有的思維規律，在反復使用中所形成的比較穩定的、定型化了的思維路線、方式、程序、模式，在感性認識階段也稱作“刻板印象”。思維定勢對學生的數學學習有積極的一面，但也有消極的一面。以下從順序性心理、停留心理和負遷移三個方面分析由思維定勢帶來的一些錯誤。

（一）順序性心理

根據信息加工理論的觀點，學習過程分為注意、編碼、儲存和提取等幾個心理過程。而信息的儲存需要進行編碼，編碼的基本要求是信息順序化。學生在解決數學問題時，常常由于順序心理導致錯誤，究其原因，是因為學生頭腦中不但存在著和問題密切相關的舊知識，而且還存在著一些固有順序，形成了一系列的順序心理，從而一些逆序性的變化就遭到原有順序心理的抗拒。[7]如在學習分數的初步認識時，一些學生常常把二分之一寫成“”，這和學生頭腦中原有的 “從上到下”的順序有關，在讀到“二”時把相應的“2”寫在分數線的上面，讀到“一”時把相應的“1”寫在分數線的下面;還有一種常見的題：湖面上有一些天鵝，飛走了5只，還剩23只，問湖面上原來有多少只天鵝？本題期望學生用加法“5+23=28”，可許多學生偏偏列出減法算式“28-5=23”，當然這并不能說是錯誤，但從中折射出一些問題，學生頭腦中的閱讀順序是“從左到右”，因此列式時也按照“從左到右”的順序。

（二）停留心理

停留心理是當概念擴展，學生的思維產生惰性，仍然停留在原來的地方，[8]這種心理實質是由學生先前的學習對后繼學習的影響而產生的，是思維定勢消極性的表現。南京師范大學李善良教授在讓300名六年級小學生判斷“2個數的積與這2個數的差（0除外）在任何情況下都不會相等”時，只有41人（14%）給出正確答案，[9]原因是學生的思維停留在自然數中，沒有考慮到分數、小數，李善良將其稱為思維“戀舊”。與之類似的有許多，如用“5，5，5，1”四張牌算出24，學生經過反復嘗試，找不到算法，原因也是學生習慣的思維方式是“整數的運算”，而不習慣“分數的運算”，這道題可以把5看作25個，可以得（5-1÷5）×5=24。這類錯誤產生的原因是學生試圖在過于限制的領域內建立聯系。

（三）負遷移

學習遷移是指一種學習影響另一種學習，也是指學得的經驗運用到新的情境中去。如果一種學習對另一種學習起到干擾或抑制作用，這就是負遷移。負遷移引起的錯誤也是思維定勢副作用的表現，常發生在具有“共同因素”的數學學習上。當新舊知識結構十分相似（但實質不同）而要求做出不同反應時，學生習慣于已有的舊知識，總希望將新知識納到舊知識的經驗系統中去，這樣就容易產生負遷移。

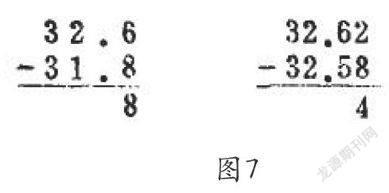
在小數的學習中，由于小數與整數“形似”，學生便會把整數的學習方法遷移到小數中，從而出現許多錯誤：如將整數讀法遷移到小數讀法中，把65.65讀作“六十五點六十五”;在小數加減法中，會把兩個數的末尾數字對齊，這是受整數加減法“把末尾對齊”的影響。另外，受整數計算的影響，學生往往會在計算結果里漏掉點小數點和用零補足數位，如圖7;在小數除法中，把56÷0.1計算成5.6，學生在之前的整數學習中，除以一個數計算結果就是縮小，而相應的乘一個數就擴大。學生把這個結論遷移到小數中，但它對于小數不完全成立，小數中存在小于1的數，一個數除以小于1的數，商是擴大的，而乘一個小于1的數，積則是縮小的。

圖7

四、喜歡簡便計算

情感在認知的基礎上產生，又對認知產生巨大的影響，成為調節和控制認知活動的一種內在因素。學生產生錯誤除了有認知方面的不足，還存在情感方面的原因。意大利學者Giorgio T.Bagni對學生錯誤原因的分析比較注重心理方面的情感因素，認為學生出現錯誤主要有以下兩個方面：首先，學生喜歡簡單的、容易的和著名的方法、思想;其次，學生害怕困難的東西，害怕題目無解。[10]正因為在計算過程中，學生喜歡用簡單、容易的方法很快算出結果，因此常常盲目地湊整，從而忽略運算順序、計算法則等規定，這類錯誤具有一定的普遍性，存在于整數、分數、小數計算中。圖8中學生看到235和65可以湊成整數“300”，便不顧運算先后順序，先計算兩者之和;圖9中學生看到3和2可以湊成整數“6”，就急于把這兩個數加起來;圖10學生看到0.25乘4可以湊成整數“1”，變得比較興奮，就把這兩個數先結合起來。

圖8

圖9

圖10

相對于喜歡簡便計算，學生害怕一些困難的東西，因此當遇到計算題中的數據較大、算式較為陌生、算式的外形過于繁雜時，就會產生排斥、厭惡心理，從而不能耐心審題、認真分析，不能選擇合理的算法，在這樣一種怕難怕繁的心態下進行計算，錯誤率就會大大提升。

學生出現的錯誤形形色色，造成錯誤的原因也千差萬別，以上造成學生出現錯誤的心理原因并非孤立存在的，而是互相影響、互相聯系的。犯錯誤是人類的天性，只有通過錯誤，人們才會不斷成長，并從中收獲智慧。“變教為學”需要教師認真對待學生的錯誤，切不可把錯誤籠統地歸為“馬虎、粗心大意”，任何真正的認識都是以主體已有的知識和經驗為基礎的主動建構，因此，盡管相應思想可能是錯誤的或幼稚的，但卻仍有一定的合理性，教師不應對此采取簡單否定的態度，而應從本質上分析錯誤產生的原因，并對其加以合理利用。顯然，也只有這樣，教師才可能采取適當的補救措施實現“變教為學”中的“助學”。

參考文獻：

[1] Hendrik Radatz. Error Analysis in Mathematics Education[J]. Journal for Research in Mathematics Education，1979，10（3）：168.

[2] Percival M.Symonds. The Psychology of Errors in Algebra[J]. The Mathematics teacher，1922，15（2）：101.

[3] Hendrik Radatz. Error Analysis in Mathematics Education [J]. Journal for Research in Mathematics Education，1979，10（3）：167.

[4] Hitch GJ. The role of short-term working memory in mental arithmetic[J]. Cognitive Psychology，1978，10：302-323.

[5] Michel Fayol， Abdi，Gombert. Arithmetic Problems Formulation and Working Memory Load[J]. Cognition and Instruction，1987，4（3）：187-202.

[6] Inez E.Berends.Van lieshout. The Effect of Illustrations in Arithmetic Problem-Solving：Effects of Increased Cognitive Load[J]. Learning and Instruction，2009，19：345-353.

[7] 楊軍，樓志權. 高中生經典數學錯誤的心理分析及對策[J]. 新疆師范大學學報（自然科學版），2007，26（3）.

[8] 付海倫. 數學語言學習中的心理性錯誤分析[J]. 數學通報，1996，（12）.

[9] 李善良. 數學概念學習中的錯誤分析[J]. 數學教育學報，2002，11（3）.

[10] Giorgio T. Bagni. An Investigation of some Misconceptions in High School Students' Mistakes Learning in Mathematics and Science and Educational Technology [M]. Cyprus Nicosia： Inter-college Press，2001.

（首都師范大學初等教育學院 ?100048）