從“錯誤”中生成教學資源策略例析

高建芳

[摘 要] 數學錯誤借助適當的策略可以生成教學資源. 數學教師不妨營造適宜的教學情境，引領學生尋找、交流、評價錯誤，發揮教師的主導作用和學生的主體地位，從而將數學錯誤轉化為數學價值.

[關鍵詞] 數學錯誤；教學資源；生成；尋找；評價

由于學生認知結構失衡和心理狀態的復雜性等多種因素，學生的作業出錯總是不可避免. 作為教師，如果能夠正確處理數學作業“錯誤”，將對提高學生的數學能力起著舉足輕重的作用.

梳理各種錯誤類型，我們不難發現，這些錯誤包含理解和運用數學知識的諸多問題：（1）思維誤區；（2）心理障礙；（3）熟練程度不夠；（4）綜合性分析能力欠缺；（5）作業設置超出學生的認知水平等. 可見，排除了這些錯誤，就意味著學生能夠進入“山重水復疑無路，柳暗花明又一村”的境界，能夠極大地提高數學成績. 因此，這些資源極有教學價值. 心理學家蓋耶認為：“誰不考慮嘗試錯誤，不允許學生犯錯誤，就將錯過最富成效的學習時刻. 我們要善待學生的‘錯誤，抓住這種數學教育契機，讓錯誤變成寶貴的教學資源. ”那如何生成呢？

尋找策略

尋找策略指有組織、有目的地搜尋錯誤的方式、方法. 運用這種策略可以幫助師生有趣味、有效率地快速發現數學錯誤，生成教學資源. 一般而言，數學作業的批改主體過于單一，絕大多數是由教師承擔的. 這當然可以讓教師最快速地了解學生的學習狀態，卻不能深層次地鍛煉學生，不能驅動他們的自主性. 因此，除了重大的考試、檢測外，我們完全可以放手讓學生分組批改，然后梳理、歸納錯誤. 在學生批改的過程中，一方面能檢測批改者的學習狀態，另一方面，能幫助被批改者尋找錯誤. 學生經歷了這樣的批改體驗，就等于自行構建了一個交流的公共平臺，會使他們忌諱再次出現類似的錯誤，也會極力避免簡單、低級錯誤的產生，從而悄無聲息地幫助他們建立一個良好的監督機制，約束他們盡可能地減少錯誤.

當然，教師的主導參與作用也不可省去，可以通過巡視、抽查、交流等形式幫助學生發現、歸類錯誤.

評價策略

評價策略指針對數學錯誤而展開的反饋、評價和修正等一系列行動的方式、方法. 數學作業設置的目的“不僅應當是程序性知識的簡單再現式鞏固，更應體現對‘教與‘學的診斷作用，體現在對學生認知結構‘順應的催化上”. 學生作業錯誤率在面積和題型上均呈現高比率，這說明教學改進的空間十分巨大，且必須及時采取有效的應對策略.

1. 對話交流

組織有效的對話交流平臺，能夠利用集體的智慧發現錯誤的原因，尋找避免錯誤的方法，從而修正錯誤，獲得正確的認知. 這在多層次和多元指向性的作業中尤其具有極強的有效性.

案例1？搖 如圖1所示，在矩形ABCD中，M，N分別是邊BC，AB上的點，且MN=MD，MN⊥MD，求證：AM平分∠BAD.

錯誤？搖 過點M作AD的垂線段MO，可得四邊形ABMO為矩形. 因為AM為其一條對角線，由MB⊥AB，MO⊥AD可知，MO=MB，所以AM平分∠BAO，也即平分∠BAD.

師：同學們看看，王亮（化名）這道題證明得正確嗎？

生1：不正確. 已知條件怎么沒有充分利用上去啊？

生2：不對，四邊形ABMO為矩形，這一點沒錯. 但是請問王亮，你怎么知道AM就一定平分∠BAD呢？（這位學生快速跑到講臺上，畫出一個圖形，證明王亮的證明不成立）

生3：我猜測，王亮同學一定是沒有找到合適的方法解決這個問題，或者只是通過這道題目給定的圖形相對比較特殊，使他誤以為四邊形ABMO為正方形，才犯了錯誤.

師：看來，如果給定的已知條件沒有充分使用，那么，就可以斷定解題錯誤. 不過，應該怎樣證明這道題呢？

生4：先逆向推理，假設AM為平分線，那么根據平分線的性質判斷，BM=MO. 如何證明呢？根據已知條件，MN=MD，且∠MOD與∠MBN都為直角，如果能再求出∠BMN=∠OMD，就可以證明這兩個三角形全等，進而推斷出BM=MO.

師：有了兩個條件，再找出一個條件，就可以證明它們全等了. 大家看，還有MN⊥MD這個條件沒有利用呢！

生5：明白了，利用矩形ABMO的性質和MN⊥MD這兩個條件，可以推出∠OMD=∠BMN，這樣就可以證明它們全等了.

師：對，這是“K型”問題.

該題涉及邏輯推理，跳躍性強，需要幾個轉換，具有多向性和多元性，要求學生具有較強的發散思維和綜合運用知識的能力. 學生做題想到畫輔助線，但是在利用輔助線并根據已知條件分析數學元素之間的關系時，存在一定的茫然性. 通過師生的共同診斷、分析，大家找到了病根，于是豁然開朗. 如果沒有交流，出錯的學生恐怕不能獨立解決這個問題，且使大家喪失了一次寶貴的預防錯誤產生、鍛煉分析錯誤的機會.

2. 集中糾正

對于典型錯誤，可以采取集中統一講解的方式，給予糾正，這樣可以更有效地利用錯誤，及時、高效地轉化為教學資源，使錯誤的價值集成化. 比如數學常見的錯誤有：（1）概念理解模糊；（2）誤解題意；（3）遺忘條件；（4）思路錯誤；（5）非技術性錯誤等，針對這些錯誤，可結合實際例題具體分析成因及對策.

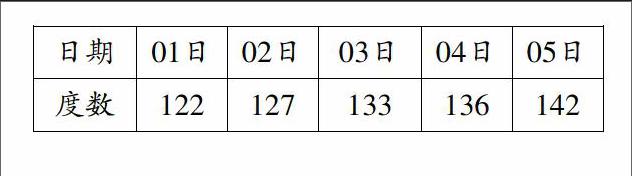
案例2？搖 耿思亮為了幫助爸爸弄清楚日平均用電量，在10月份前五天，每天準時抄錄電表，記錄情況如下：

耿思亮同學給出了他一家10月總的用電量大約為：（122+127+133+136+142）÷5×31=4092（度）.

分析？搖 這位學生由于受思維定式的影響，沒有結合生活實際情形，致使機械地按常規平均數的求解方法去審題、解題.

正解 （142-122）÷（5-1）×31=155（度）.

利用這個典型錯誤，可以有效地提醒學生要根據具體的數學情景，靈活地運用數學知識解決問題，而不能主觀臆斷.

除此之外，我們還應當要求學生自主整理典型的數學錯誤. “好記性不如爛筆頭. ”指導學生制作典型錯誤題集，能夠切實幫助學生避免再犯類似的錯誤，提高其分析問題的能力. 我們可以不定期地通過交流、抽查等形式，督促他們切實整理好. 我們本身也要不斷地反思學生錯題產生的原因，便于從源頭上解決數學知識和技能傳授上的不足.

荷蘭著名學者弗賴登塔爾說過：“反思是數學的重要活動，是數學活動的核心和動力. ”反思的內容必然也包括數學錯誤. 因此，我們力求最大可能地使學生避免錯誤的產生，同時也要有效地利用好數學錯誤.endprint