非齊次非線性擴散方程的高維不變子空間和等價變換

董亞瑩

(西北大學數學學院，陜西 西安　710127)

非齊次非線性擴散方程的高維不變子空間和等價變換

董亞瑩

(西北大學數學學院，陜西 西安710127)

利用與不變子空間方法相關的等價變換和變換v=enu給出了非齊次非線性擴散方程的等價方程，并得到了等價方程的高維不變子空間.最后給出一些例子構造了非齊次非線性擴散方程的廣義泛函分離變量解.

非線性擴散方程；不變子空間方法；等價變換；廣義泛函分離變量解

1　引言

本文研究非齊次非線性擴散方程

構造非線性演化方程

解的一種有效的方法是不變子空間法[5-6].下面介紹不變子空間法及其相關的定理和定義.

有限維線性空間稱為在給定算子 F作用下不變當且僅當 F[Wm]?Wm.這意味著存在依賴于 φi(t)的函數使得

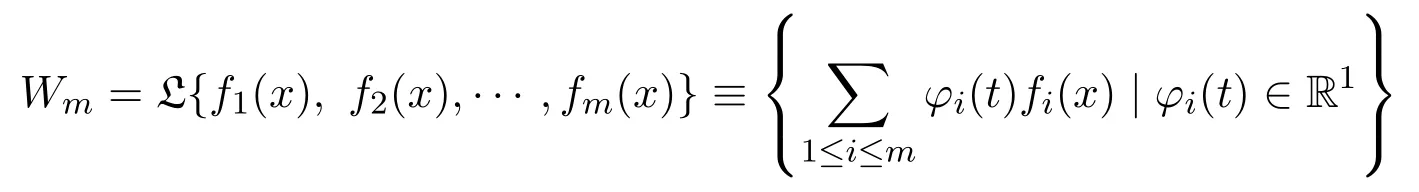
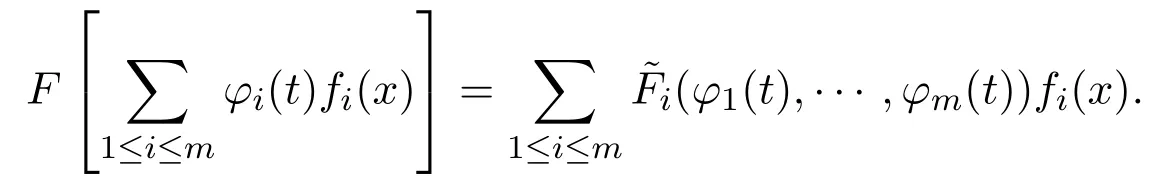
如果線性子空間Wm在給定算子F作用下不變，那么方程(2)有廣義分離變量解：

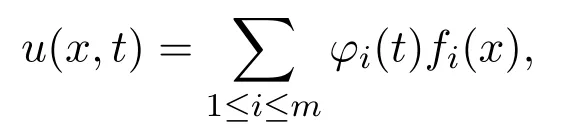
其中φi(t)(i=1，···，m)滿足有限維動力系統值得注意的是任意一個線性空間Wm=L{f1(x)，f2(x)，···，fm(x)}是由線性常微分方程

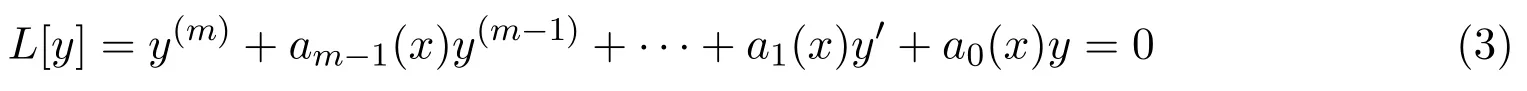
其中 [H]表示 L[u]=0及其關于 x的微分序列.由不變條件 (4)可知不變子空間與條件Lie-B?cklund對稱有關[6-14].

定理 1.1[5，7]如果由方程(3)的解空間定義的m維子空間Wm在一個k階非線性微分算子F作用下不變，那么m≤2k+1.

定義 1.1[5]如果通過變量變換

可以得到，

那么稱算子F[y]=F(x，y，y′，···，y(k))等價于算子并且，如果算子F允許不變子空間：

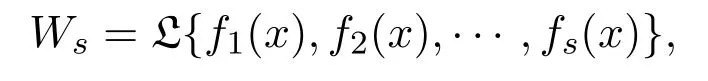
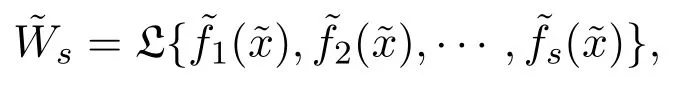
2　方程 (1)的等價方程

下面分兩種情況討論這個算子.

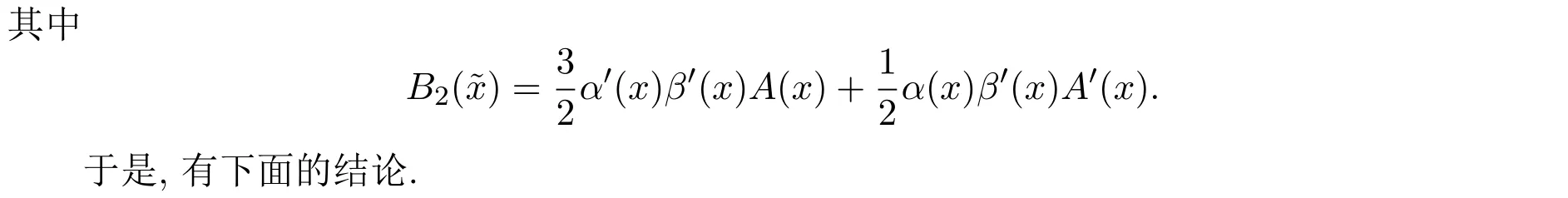
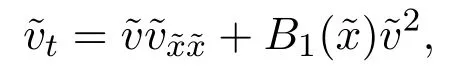
其中a是常數.

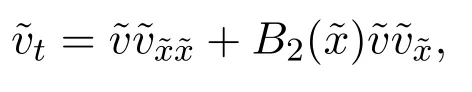
3　等價方程的高維不變子空間

由定理1.1，二階非線性微分算子允許的不變子空間的維數不超過5.因此，下面考慮微分算子(9)式和(10)式允許的2至5維不變子空間.為了方便計算，將和分別記作x和y.在本文中用記號yj=djy/dxj(j＞0，y0=y).

分別設

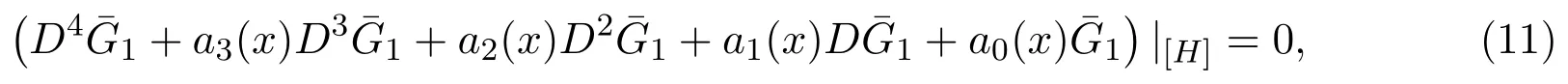
其中D是關于x的全導數.直接計算可以得到方程(11)的左邊是關于y3，y2，y1，y0的多項式，即

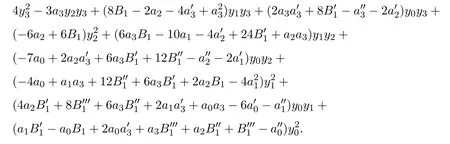
對上面多項式進行分析和計算，可以得到下面的結果.

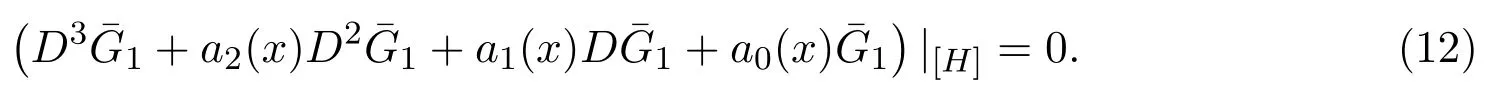
經計算可得，

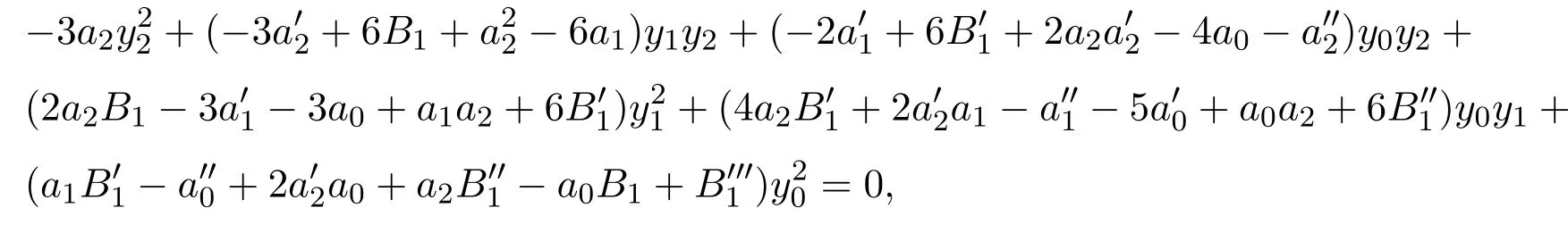
其中B1(x)，a1(x)，a2(x)滿足下列決定方程組：

由決定方程組 (13)的第一個方程得到 a2≡0.把 a2≡0代入 (13)的第二個方程，則有B1(x)=a1(x).再把B1(x)=a1(x)代入(13)的第三個、第四個和第五個方程，可以得到a′1(x)=a0(x).因此有下面的結論.

其允許的不變子空間由常微分方程

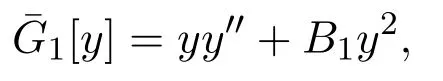
定義，其中B1(x)=a1(x)和a′1(x)=a0(x).

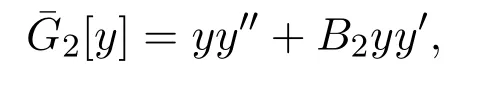
其允許的不變子空間由常微分方程 y′′′+a2(x)y′′+a1(x)y′=0定義.其中 B2(x)=a2(x) 和a′2(x)=a1(x).

相同的計算也可以得到下面的注解.

(2)如果由二階常微分方程(3)定義的不變子空間在非線性微分算子下不變，那么不變條件為：

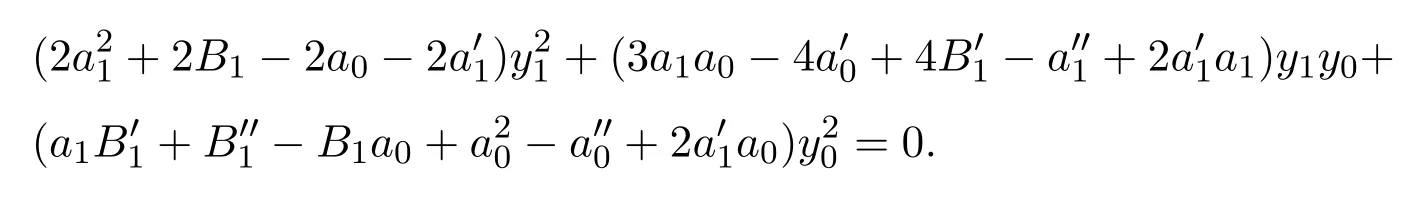
(3)如果由二階常微分方程(3)定義的不變子空間在非線性微分算子下不變，那么不變條件為：

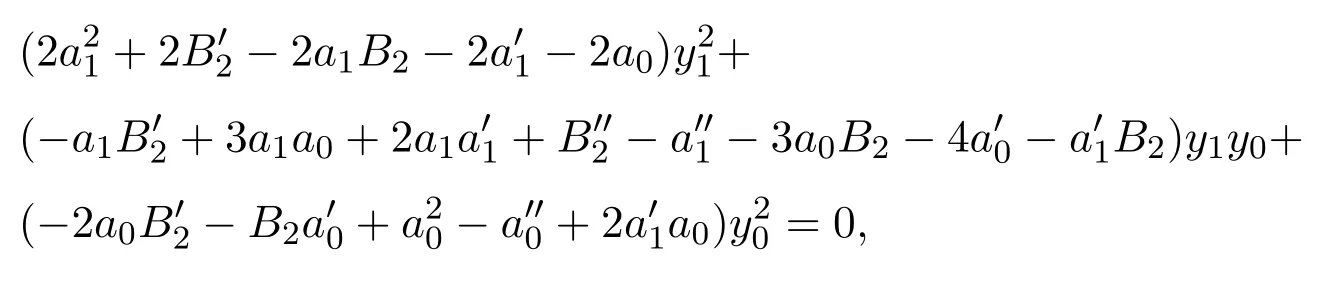
這里很難求得a0(x)和a1(x)的具體表達式.

4　方程 (1)的廣義泛函分離變量解

利用不變子空間方法和第三節中的結論，可以構造(9)式和(10)式對應的擴散方程的廣義分離變量解.進一步得到方程(1)的廣義泛函分離變量解.下面給出幾個例子說明這個方法.

例4.1通過變換v=enu，方程

例4.2通過變換v=enu，方程

例4.3利用變換v=enu和變量變換方程

5　結論

本文通過利用變換v=enu及與不變子空間方法相關的等價變換將非線性非齊次擴散方程轉化為變系數演化方程.進一步，得到了方程(1)的等價方程并且求出了等價方程的高維不變子空間.在文獻[13-15]中，變系數非線性演化方程的解是通過不變子空間和條件Lie-B?cklund對稱得到的.而在本文中，對變系數非線性演化方程，首先利用與不變子空間方法相關的等價變換降低變系數的個數.之后，利用不變子空間得到方程的解.事實上，當利用不變子空間方法解這類方程時，只需要考慮微分算子的不變子空間.這樣做的好處是能簡化計算過程.這種方法也可用于其他非線性方程.

[1]Crank J.The Mathematics of Diffusion[M].Oxford：Clarendon Press，1975.

[2]Herbert A，Bazley N，Kirchg?ssner K.Applications of Nonlinear Analysis in the Physical Science[M]. London：Pitman，1981.

[3]Berryman J G，Holland C J.Nonlinear diffusion problems arising in plasma physics[J].Phys.Rev.Lett.，1978，40(26)：1720-1722.

[4]Kamin S，Rosenau P.Propagation of thermal waves in an inhomogeneous medium[J].Comm.Pure Appl. Math.，1981，34(6)：831-852.

[5]Galaktionov V A，Svirshchevskii S R.Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics[M].London：Chapman and Hall，2007.

[6]Galaktionov V A，Vázquez J L.Geometrical properties of the solutions of one-dimensional nonlinear parabolic equations[J].Math.Ann.，1995，303(4)：741-769.

[7]Svirshchevskii S R.Lie-B?cklund symmetries of linear ODEs and generalized separation of variables in nonlinear equations[J].Phys.Lett.A，1995，199(56)：344-348.

[8]Zhdanov R Z.Conditional Lie-B?cklund symmetry and reductions of evolution equations[J].J.Phys.A，1995，28(13)：3841-3850.

[9]Fokas A S，Liu Q M.Nonlinear interaction of traveling waves of nonintegrable equations[J].Phys.Rev. Lett.，1994，72(21)：3293-3296.

[10]Qu C Z，Ji L N.Invariant subspaces and conditional Lie-B?cklund symmetries of inhomogeneous nonlinear diffusion equations[J].Sci.China Math.，2013，56(11)：2187-2203.

[11]Ji L N.Conditional Lie-B?klund symmetries and functionally generalized separable solutions to the generalized porous medium equations with source[J].J.Math.Anal.Appl.，2012，389(2)：979-988.

[12]Ji L N.Conditional Lie-B?cklund symmetries and solutions of inhomogeneous nonlinear diffusion equations[J].Phys.A，2010，389(24)：5655-5661.

[13]Feng W，Ji L N.Conditional Lie-B?cklund symmetries and functional separable solutions of generalized inhomogeneous diffusion equations[J].Phys.A，2013，392(4)：618-627.

[14]姬麗娜，張穎.多孔介質方程的廣義條件對稱的精確解[J].純粹數學與應用數學，2011，27(3)：339-342.

Equivalent transformations and higher-dimensional invariant subspaces to the inhomogeneous nonlinear diffusion equations

Dong Yaying
(College of Mathematics，Northwest University，Xi′an710127 China)

In this paper，we firstly obtain the equivalent equations of the inhomogeneous nonlinear diffusion equations by the transformation v=enuand equivalent transformations related to invariant subspace method. Moreover，higher-dimensional invariant subspaces of equivalent equations are derived.Finally，some examples are presented and the generalized functional separable solutions of the inhomogeneous nonlinear diffusion equations can be constructed.

nonlinear diffusion equations，invariant subspace method，equivalent transformations，the generalized functional separable solutions

O175.2

A

1008-5513(2015)01-0018-09

10.3969/j.issn.1008-5513.2015.01.003

2014-10-10.

國家自然科學基金(11371293).

董亞瑩(1988-)，博士生，研究方向：偏微分方程.

2010 MSC:35A22，35A25，35A55