一個修正Novikov方程弱解的全局存在性

李騰龍，王祥，黃晴

(西北大學數學學院，陜西 西安　710127)

一個修正Novikov方程弱解的全局存在性

李騰龍，王祥，黃晴

(西北大學數學學院，陜西 西安710127)

主要研究了一個修正的Novikov方程，并給出了當初值u0(x)滿足一定條件時，方程弱解的全局存在性，推廣了Novikov方程的相關結果.

修正Novikov方程；弱解；全局存在性

1　前言和主要結果

2009年，Vladimir Novikov[1]在非局部偏微分方程的對稱分類中得到了一個具有三次非線性項的可積方程(簡稱為Novikov方程)，形式如下：

該方程具有Lax對、雙 Hamilton結構、無窮多守恒量以及尖峰波解，且其 Cauchy問題在Besov空間及Sobolev空間 Hs(s＞3/2)中的局部適定性、解的持續性以及爆破現象[2-5]、整體弱解的存在唯一性[6-7]及周期Novikov方程的局部適定性[8]已有一些結果.

2010年，趙磊和周水庚在文獻 [9]中對該方程進行改良，用更高次的 u4ux代替原有的u2ux，從而得到了修正的Novikov方程(簡稱mN方程)：

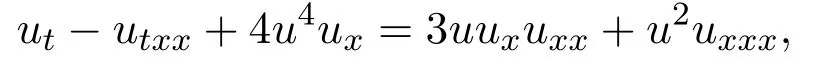
并找到了方程的孤立波解.

本文主要考慮修正的Novikov方程弱解的全局存在性.

考慮如下方程的Cauchy問題：

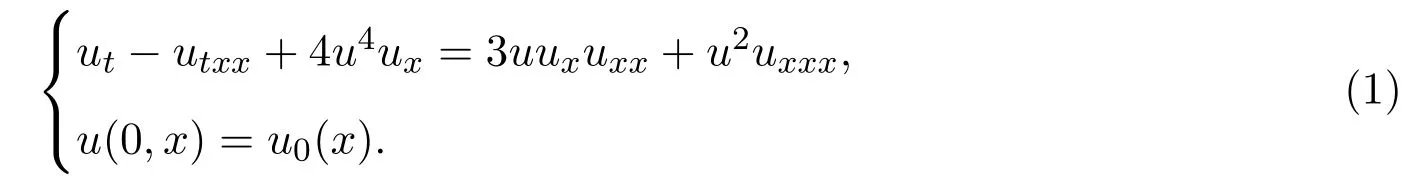
利用算子Λ2=1??2x，可將方程(1)化為：

(iii)在分布意義下，u=u(t，x)滿足方程(2)且逐點滿足初值條件；則稱u(t，x)為方程的弱解.

本文的主要結論是：

2　Cauchy問題(2)的粘性逼近方法

定義函數：

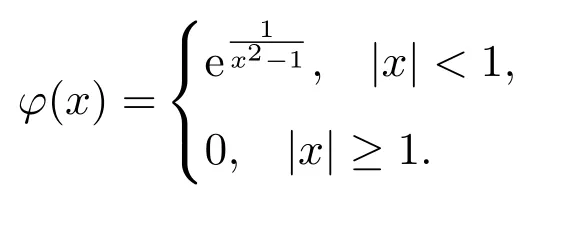
選取如下磨光函數：

對初值u0(x)進行磨光，可得

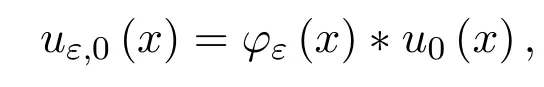
由文獻[10]知，uε，0(x)∈C∞(R)且有：

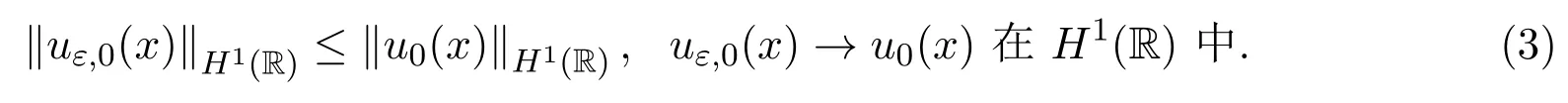
考慮Cauchy問題(2)的粘性逼近方程：

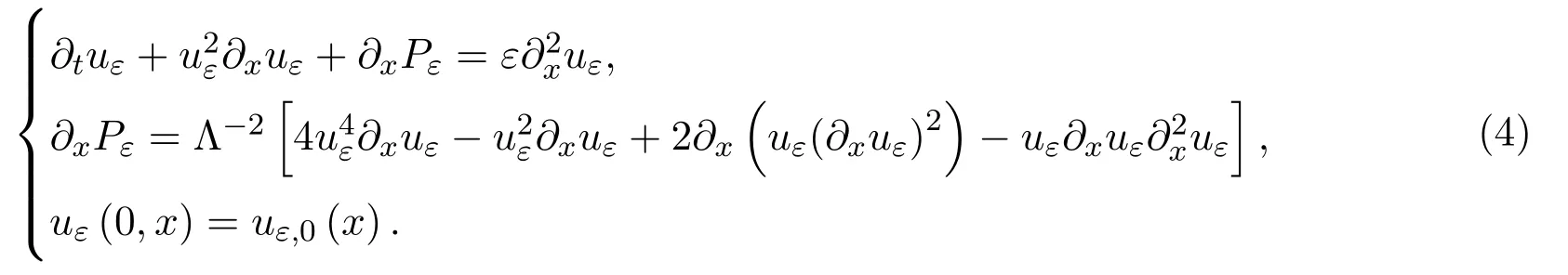
對方程(4)關于x求偏導，并設qε=?xuε，得到：

3　引理

引理3.1若u0(x)∈H1(R)，則對任意的α≥3，Cauchy問題(4)存在唯一的解uε(t，x)，滿足uε∈C([0，+∞)；Hα(R))，另外，對t＞0，有：

推論3.1若u0∈H1(R)，則

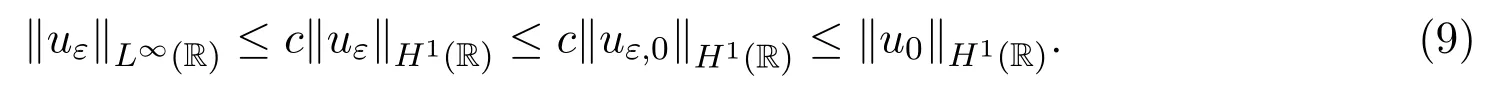
引理 3.2若0＜ε＜1/4，0＜t＜T，uε為Cauchy問題(4)的唯一解，則存在正常數

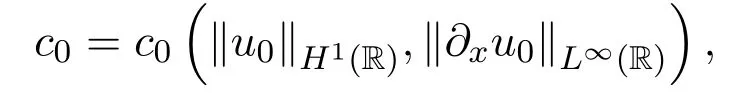
滿足：

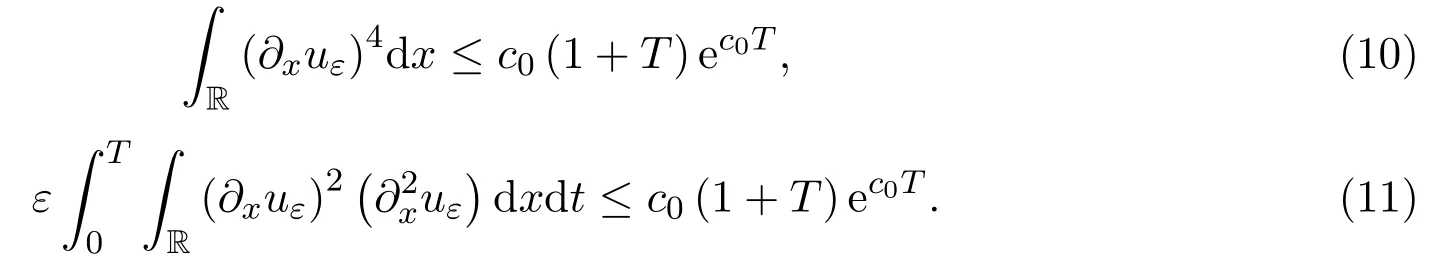
引理 3.3uε=uε(t，x)為Cauchy問題(4)的唯一解，對于任意的0＜t＜T，則存在與ε無關的正常數滿足：

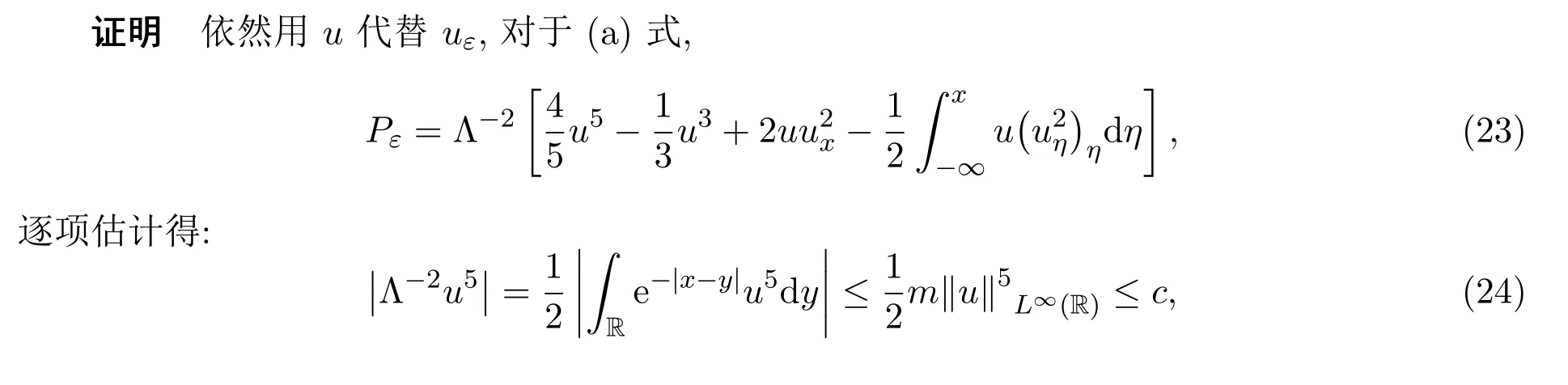
利用同樣方法可得Q的結論，證明從略.

引理3.4若u0(x)∈H1(R)，u0(x)≥0，uε(t，x)為Cauchy問題(4)的解，則uε(t，x)≥0.

證明由引理3.3知Cauchy問題(4)滿足拋物方程的極值原理，因為u0(x)≥0，故而uε，0(x)≥0，由極值原理得uε(t，x)≥0.

應用文獻[8]中的方法可以得到如下的兩個引理：

引理3.5設uε=uε(t，x)為Cauchy問題(4)的弱解，且定理1.1中的條件成立，則存在正常數c=c0(1+T)ec0T，使得

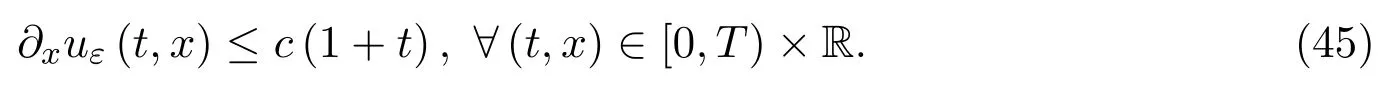
引理3.6設uε=uε(t，x)為Cauchy問題(4)的弱解，且定理1.1中的條件成立，則存在子列{εj}j∈N→0和u∈L∞([0，∞)；H1(R))∩H1([0，T]×R)滿足：

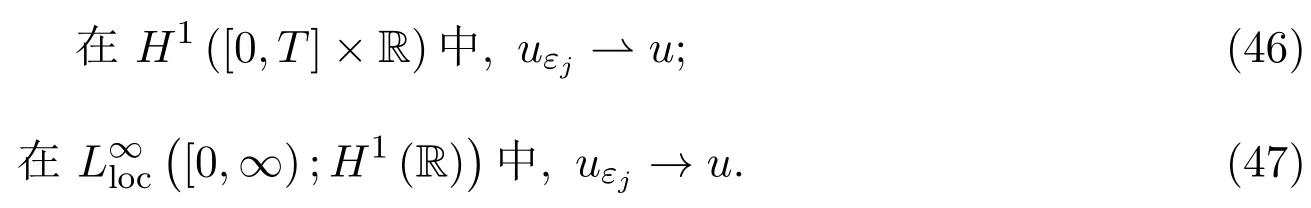
引理 3.7函數序列{Qε(t，x)}在空間中一致有界，且存在一個子函數列和函數對任意的1＜p＜∞，使得

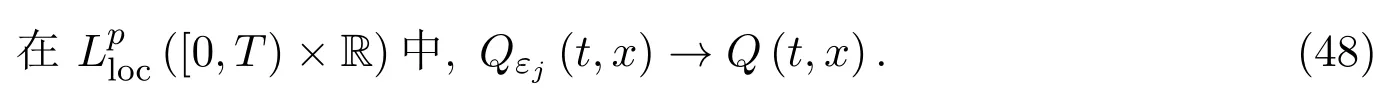
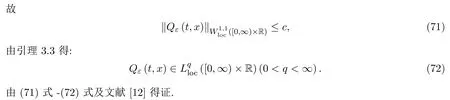
類似于文獻[7]的證明，有如下兩個引理：

引理3.8存在子列{εj}j∈N→0和兩個函數

其中1＜p＜4，1＜r＜2，滿足：

4　定理1.1的證明

由(3)式、(9)式以及引理3.6得，

由引理3.6、引理3.7及引理3.9得u在分布意義下滿足Cauchy問題(2)，由引理3.2和引理3.5得到u滿足性質(a)和(b).

[1]Novikov V S.Generations of the Camssa-Holm equation[J].J.Phys.，2009，342：11-32.

[2]Yan W，Li Y S，Zhang Y M.Global existence and blow up phenomena for the weakly disspative Novikov equation[J].Nonlinear Analysis，2012，75：2464-2473.

[3]Yan W，Li Y S，Zhang Y M.The Cauchy problem for the integrable Novikov equation[J].Journal of Differetial Equation，2012，253：298-318.

[4]Jiang Z H，Ni L D.Blow-up phenomenon for the integrable Novikov equation[J].Journal of Mathematical Analysis and Applications，2012，385：551-558.

[5]Ni L D，Zhou Y.Well-posedness and persistence properties for the Novikov eqution[J].J.Differential Equation，2011，250：3002-3021.

[6]Wu X L，Yin Z Y.Global weak solutions for the Novikov equation[J].Journal of Physics A：Mathematical and Theoretical，2011，55：44-68.

[7]Lai S Y.Global weak solutions for the Novikov eqution[J].Journal of Functional Analysis，2013，265：520-544.

[8]Tiglay F.The periodic Cauchy problem for Novikov equation[J].International Mathematics Research Notices，2011，20：4633-4648.

[9]Zhao L，Zhou S.symbolic analysis ans exact travelling wave solutions to a new modified Novikov equation[J]. Appl.Math.Comput.，2010，217：590-598.

[10]Lai S Y，Li N，Wu Y H.The local well-posedness and existence of weak solutions for a generalized Camassa-Holm equation[J].J.Differential Equation，2010，248：2038-2063.

[11]Coclite G M，Holden H，Karlsen K H.Well-posedness for a parabolic-elliptic system[J].Discrete Contin. Dyn.Syst.，2005，13：659-682.

[12]Simon J.Compact sets in the space Lp((0，T)；B)[J].Ann.Mat.Pura.Appl.，1987，146：65-96.

The existence of the global weak solution to a modified Novikov equation

Li Tenglong，Wang Xiang，Huang Qing

(College of Mathematics，Northwest University，Xi′an710127，China)

In this paper，we study a modified Novikov equation and also obtain the existence of the global weak solution to the modified Novikov equation if the initial data u0(x)satisfies some certain conditions.The results improve the relative ones as well.

modified Novikov equation，weak solution，global existence

O175.2

A

1008-5513(2015)01-0053-12

10.3969/j.issn.1008-5513.2015.01.007

2014-10-23.

國家自然科學基金(11101332).

李騰龍(1989-)，碩士生，研究方向：偏微分方程.

2010 MSC:35A25