修正的廣義Vakhnenko方程的周期解

聶顯佳，張巖，扎其勞

(內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古 呼和浩特　010022)

修正的廣義Vakhnenko方程的周期解

聶顯佳，張巖，扎其勞

(內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古 呼和浩特010022)

利用Hirota雙線性方法以及Rienmann theta函數(shù)，構(gòu)造了含兩個任意常系數(shù)的修正的廣義Vakhnenko方程的周期解.特別是在極限情況下，可以由方程的周期解得到其孤子解.

周期解；Rienmann theta函數(shù)；修正的廣義Vakhnenko方程

1　引言

近年來許多學(xué)者利用Hirota雙線性方法和Rienmann theta函數(shù)來求解非線性演化方程，特別是孤子方程的周期解.Rienmann theta函數(shù)最初是由德國數(shù)學(xué)家Rienmann在研究普通函數(shù)時，將函數(shù)概念推廣到多值函數(shù)并引進(jìn)了多葉Rienmann曲面的直觀概念中提取出來的. Theta函數(shù)是多復(fù)變特殊函數(shù)的一種，具有很好的擬周期性.到了70年代，文獻(xiàn)[1-2]在雙線性方法的基礎(chǔ)上，結(jié)合Rienmann theta函數(shù)求得了一系列孤子方程的周期解，且得到的多周期解取極限形式可以退化到孤子，不需要通過散射理論而直接求得方程的顯示解，因此也被稱為直接法，該方法主要是通過引入雙線性D算子來實現(xiàn)的，從而可以將非線性演化方程化為相應(yīng)的雙線性方程.一旦雙線性方程被確定，求其精確解的過程就變得簡單.這種方法直接有效而且周期解中的所有參數(shù)都是可以任意選取的.從方程的周期解出發(fā)，可以清晰的描述和分析出影響非線性方程隨時間運動的幾個重要參數(shù)之間的關(guān)系：例如振幅、波速以及運動方向之間的關(guān)系.所以研究周期解對非線性方程具有很好的價值.本文利用Hirota雙線性方法[3]以及Rienmann theta函數(shù)，研究修正的廣義Vakhnenko方程(mGVE)(見文獻(xiàn)[4])的周期解.

修正的廣義Vakhnenko方程以及廣義Vakhnenko方程(GVE)(見文獻(xiàn)[5])是Vakhnenko方程(VE)(見文獻(xiàn)[6])的擴展形式，mGVE的形式為：

其中α和β是任意常數(shù).當(dāng)α=1時，方程(1)簡化為GVE；當(dāng)α=1，β=0時，方程(1)簡化為VE.關(guān)于方程VE、GVE和mGVE的多孤子解已有許多研究結(jié)果[4-10].

2　mGVE的變換

根據(jù)文獻(xiàn)[3-9]，引入獨立變量X和T，定義為：

3　mGVE的周期解

由以上的分析，考慮雙線性方程(7)的多維Rienmann theta函數(shù)解：

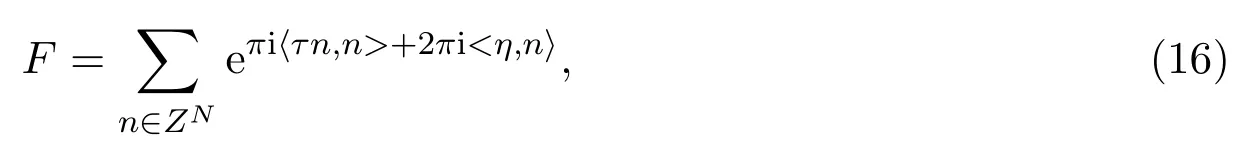
其中n=(n1，···，nN)T∈ZN，η=(η1，···，ηN)，〈·，·〉是兩個向量的內(nèi)積，τ是一個對稱矩陣且 Im|τ|＞0，ηj=kjX+ωjT+η(0)j，j=1，···，N.

現(xiàn)在，將給出方程(1)的1-周期解和2-周期解.

3.1 1-周期解及漸進(jìn)性

3.22-周期解及漸進(jìn)性

現(xiàn)在考慮mGVE的2-周期解，當(dāng)N=2時，方程(16)可以化為：

那么線性系統(tǒng)(41)有唯一的非零解(ω1，ω2，c).求解此系統(tǒng)，可以得到方程(7)的2-周期解：其中F和ω1，ω2，c分別滿足(35)式和(41)式，這里k=(k1，k2)是由(42)式?jīng)Q定的.然后通過方程(9)，將得到U，所以 mGVE的2-周期解可以由(12)式和(13)式及W 和U給出.圖2-圖3給出了滿足相應(yīng)的參數(shù)條件時相應(yīng)方程的2-周期解的圖像.

圖2　mGVE方程的2-周期解，參數(shù)選為：α=6，β=2，k1=2，k2=?2，τ11=2.4i，τ12=1.2i，τ22=3i

圖3　mGVE方程的2-周期解，參數(shù)選為：α=6，β=2，k1=2，k2=?2，τ11=2.8i，τ12=1.4i，τ22=i.

其證明與公式(34)的證明類似.然后通過方程(5)，將得到U，所以mGVE的2-孤子解可以由(12)式和(13)式及W 和U給出.

4　結(jié)論

眾所周知，Hirota雙線性方法是構(gòu)造非線性波方程顯式解的最有效方法之一.本文首先利用Hirota雙線性方法和一組變換給出mGVE的N孤立子解，然后利用Riemann theta函數(shù)構(gòu)建了它的周期解.所用的方法具有普遍意義，利用它也可以得到其它非線性演化方程的周期解.在極限情況下，可以退化為孤子解.

[1]Nakamura A.A direct method of caculating periodic wave solutions to nonlinear evolution equations.I. exact two-periodic wave solution[J].J.Phys.soc.Jpn.，1979，47：1701-1705.

[2]Nakamura A.A direct method of caculating periodic wave solutions to nonlinear evolution equations. II.exact one-and two-periodic wave solution of the coupled bilinear equations[J].J.Phys.soc.Jpn.，1980，48：1365-1370.

[3]Hirota R.The Direct Method in Soliton Theory[M].Cambridge：Cambridge University Press，2004

[4]Morrison A J，Parkes E J.The N-soliton solution of the modified generalized Vakhnenko equation(a new nonlinear evolution equation)[J].Chaos Solitons Fractals，2003，16：13-26.

[5]Vakhnenko V O，Parkes E J.Morrison，B?cklund transformation and the inverse scattering transform method for the generalized Vakhnenko equation[J].Chaos Solitons Fractals，2003，17：683-692.

[6]Vakhnenko V O.Solitons in a nonlinear model medium[J].J.Phys.A：Math.Gen.，1992，25：4181-4187.

[7]Wazwaz A M.N-soliton solutions for the Vakhnenko equation and its generalized forms[J].Phys.Scr.，2010，82：065006.

[8]Wu Y，Wang C，Liao S J.Solving the one-loop soliton solution for the vakhnenko equation by means of the homotopy analysis method[J].Chaos Solitons Fractals，2005，23：1733-1740.

[9]El-Nahhas A.Analytic approximation for the one-loop soliton solution of the Vakhnenko equation[J]，Chaos Solitons Fractals，2009，40：2257-2264.

[10]Li B，Ma Y，Sun J.The interaction process of the N-soliton solution for an extand generalization of Vakhnenko equation[J].Appl.Math.Comput.，2010，216：3522-3535.

Periodic wave solutions for the modified generalized Vakhnenko equation

Nie Xianjia，Zhang Yan，Zha Qilao
(College of Mathematics Science，Inner Mongolia Normal University，Huhhot010022，China)

The new periodic wave solution for the modified generalized Vakhnenko equation is presented by using Hirota method and Rienmann theta function，from which the soliton solution can be obtain via an appropriate limited procedure.

periodic solution，Rienmann theta function，modified generalized Vakhnenko equation

O175.2

A

1008-5513(2015)01-0043-10

10.3969/j.issn.1008-5513.2015.01.006

2014-11-10.

國家自然科學(xué)基金(11261037)；內(nèi)蒙古自治區(qū)“草原英才”培養(yǎng)項目(CYYC2011050)；內(nèi)蒙古自治區(qū)高等學(xué)校“青年科技英才支持計劃”青年科技領(lǐng)軍人才項目(2014MS0111)；內(nèi)蒙古自治區(qū)自然科學(xué)基金(2014MS0111)；內(nèi)蒙古自治區(qū)人才開發(fā)基金.

聶顯佳(1989-)，碩士生，研究方向：非線性數(shù)學(xué)物理與符號計算.

扎其勞(1971-)，博士，教授，研究方向：孤立子理論和可積系統(tǒng)理論.

2010 MSC:35J15