某些完全正則半環(huán)的刻畫

賈麗，喬占科

(蘇州科技學(xué)院數(shù)理學(xué)院，江蘇 蘇州　215009)

某些完全正則半環(huán)的刻畫

賈麗，喬占科

(蘇州科技學(xué)院數(shù)理學(xué)院，江蘇 蘇州215009)

研究了完全正則半環(huán)的特征.利用半群的方法，得到了當分配半環(huán)的乘法冪等元集分別是左零帶、矩形帶以及正規(guī)帶時，該類半環(huán)成為完全正則半環(huán)的等價刻畫，推廣并改進了相關(guān)文獻的主要結(jié)果.

分配半環(huán)；完全正則半環(huán)；完全單半環(huán)；半環(huán)同余

1　引言及預(yù)備知識

半環(huán)(S，+，·)是一個代數(shù)結(jié)構(gòu)，它包含一個非空集合S，在S上定義兩個二元運算“+”與“·”，使得(S，+)和(S，·)均為半群，且滿足下列分配律：

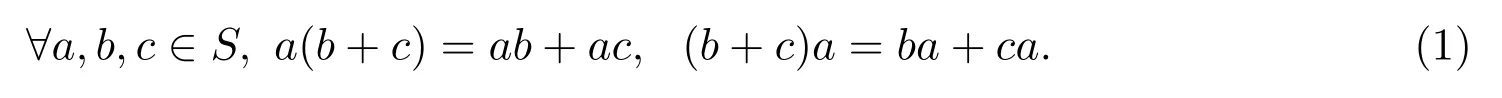
若半環(huán)(S，+，·)滿足對偶于(1)式的分配律：

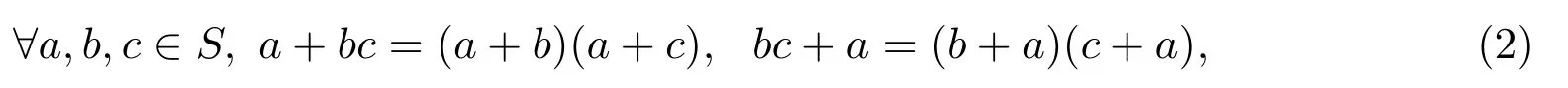
則稱(S，+，·)為分配半環(huán).

在半環(huán)理論中，半環(huán)特征的刻畫是半環(huán)研究中的一個熱點.文獻[1]匯集了完全正則半群的當代主要研究成果.半群(S，·)是完全正則的，是指?a∈S，?x∈S，使得a=axa，ax=xa.文獻[2-5]對冪等分配半環(huán)簇進行了深入的研究，獲得了一系列非常有意義的工作.文獻[6-7]分別對半環(huán)的乘法半群和加法半群進行了研究，得到了這類半環(huán)的性質(zhì)和特征.從這些研究成果中可看到半群中使用的方法對研究半環(huán)也是十分重要的.文獻[8]對加法半群為左零半群的半環(huán)成為完全正則半環(huán)進行了研究，并給出了其等價刻畫.但在該文的條件下，商半環(huán)(S/˙ J，+，·)實際上是只有一個元的半環(huán)，這是一種極為特殊的情形.本文對文獻[8]的條件進行了改進，給出了完全正則半環(huán)的刻畫，并對乘法冪等元的幾種特殊情況進行了討論，得到了若干結(jié)果.本文中其它未說明的記號和術(shù)語參見文獻[1，9].

2　主要結(jié)果及其證明

定義2.1[8]在半環(huán)(S，+，·)中，若半群(S，·)是完全正則半群，則稱(S，+，·)是完全正則半環(huán).若半群(S，·)是完全單半群，則稱(S，+，·)是完全單半環(huán).

定義2.2[8]在半環(huán)(S，+，·)中，若ρ同時為半群(S，+)，(S，·)上的同余，則稱ρ為半環(huán)S上的半環(huán)同余.

定義2.3在半環(huán)(S，+，·)中，設(shè)ρ是半環(huán)同余，若半群(S/ρ，+)，(S/ρ，·)都為帶(即冪等元半群)，則稱ρ為冪等半環(huán)同余.

Green-關(guān)系對半群理論有著重要的作用，而半環(huán)是由分配律聯(lián)系著的兩個半群，故Green-關(guān)系當然對半環(huán)的研究也是非常有用的.

首先給出一個重要引理.

引理 2.1[1]若(S，·)是完全正則半群，則格林關(guān)系J是S上的最小半格同余.

以下是本文的主要結(jié)果：

定理 2.1設(shè)(S，+，·)是分配半環(huán)，E[+]，E[[+]=E[·]，則(S，+，·)是完全正則半環(huán)當且僅當(S，+，·)為完全單半環(huán)的冪等半環(huán).

定義2.4在半環(huán)(S，+，·)中，設(shè)ρ為(S，+，·)上的半環(huán)同余，T是一個帶類(即冪等元半群類).若商半群(S/ρ，+)，(S/ρ，·)都屬于T，則稱ρ是一個T帶同余.此時稱半環(huán)(S/ρ，+，·)是一個T帶半環(huán).其中T可以是半格類、矩形帶類、正規(guī)帶類等.進一步，可得到：

定理 2.2設(shè)(S，+，·)是分配半環(huán)，E[+]，E[[+]=E[[+]可交換，則(S，+，·)是完全正則半環(huán)當且僅當(S，+，·)為完全單半環(huán)的半格半環(huán).

反過來，若(S，+，·)是完全單半環(huán)的半格半環(huán)，則(S，+，·)顯然是完全單半環(huán)的冪等元半環(huán).由定理2.1知，(S，+，·)是完全正則半環(huán).

由于冪等元的類型對半環(huán)的研究具有一定的影響，下面給出分配半環(huán)在其冪等元集的不同類型下成為完全正則半環(huán)的等價刻畫.

定理 2.3設(shè)(S，+，·)是分配半環(huán)，E[+]，E[[+]=E[·]，E[·]是左零帶，則(S，+，·)是完全正則半環(huán)當且僅當(S，+，·)是完全單半環(huán)的左零帶半環(huán).

由以上定理，直接可以得出：

推論 2.1設(shè) S是分配半環(huán)，E[+]，E[[+]=E[·]，E[·]是矩形帶，則S是完全正則半環(huán)當且僅當S是完全單半環(huán)的矩形帶半環(huán).

推論 2.2設(shè) S是分配半環(huán)，E[+]，E[[+]=E[·]，E[·]是正規(guī)帶，則S是完全正則半環(huán)當且僅當S是完全單半環(huán)的正規(guī)帶半環(huán).

[1]Petrich M.A Structure Theorem for Compeletely Regular Semigroups[M].Proceedings of the American Mathematical Society，1987.

[2]Pastijn F.Idempotent distributive semirings II[J].Semigroup Forum.，1983，26(1)：151-166.

[3]Sen M K，Guo Yuqi，Shum K P.A class of Idempotent Semirings[J].Semigroup Forum.，2000，60(3)：351-367.

[4]Zhao Xianzhong.Idempotent semirings with a commutative additive reduct[J].Semigroup Forum.，2002，64(2)：289-296.

[5]Pastijn F，Guo Yuqi.The lattice of idempotent distributive semiring varieties[J].Science in China，1999，42(8)：785-804.

[6]潘秀娟，邵勇，田俊華.乘法半群為正規(guī)純正群的半環(huán)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)，2005，21(1)：76-79.

[7]王亞芹.加法半群為正規(guī)純正群的半環(huán)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué)，2007，23(1)：66-70.

[8]龔路，李剛.加法為左零半群的完全正則半環(huán)[J].科學(xué)技術(shù)與工程，2008，8(20)：5635-5636.

[9]Howie J M.An Introduction to Semigroup Theory[M].New York：Academic Press，1976.

The characterizations of some completely regular semiring

Jia Li，Qiao Zhanke
(College of Mathematics，Suzhou University of Science and Technology，Suzhou215009，China)

In this paper，we study the characteristics of completely regular semirings.Using the methods of semigroups，we obtain the equivalent characterizations of distributive semirings whose sets of multiplication idempotents are left zero bands，rectangular bands or normal bands，we also promote and improve the main results of revelant papers.

distributive semirings，completely regular semirings，completely simple semirings，semiring congruence

O153.3

A

1008-5513(2015)01-0093-04

10.3969/j.issn.1008-5513.2015.01.011

2014-06-12.

賈麗(1990-)，碩士生，研究方向：代數(shù)學(xué).

2010 MSC:20M99