滬深300股指期貨日歷效應研究

陳雁

【摘要】 本文將滬深300股指期貨作為研究的對象，研究其日歷效應。我們用同花順軟件選取樣本數據，并且應用EXCEL、SPSS、EVIEWS等軟件對數據進行處理。在此基礎上，運用ARCH模型和GRCH模型進行實證檢驗，最后發現滬深300股指期貨存在收益率在星期一顯著為負，在星期五顯著為正數的周內效應的結論。并在該研究結論的基礎上提出了針對性的政策建議。

【關鍵詞】 滬深300股指期 貨日歷效應 ARCH模型

一、引言

股指期貨在我國已經經歷了四年多發展，滬深300股指期貨不僅開啟了中國金融期貨的時代，也豐富了我國在證券市場上的交易種類，使得金融市場更加健全，但仍然存在著各種市場異象。這些異象的存在一方面嚴重影響了市場的有效性，另一方面也給投資者帶來巨大的風險。其中主要的異象之一就是日歷效應（Calendar Effect），即市場收益率在某一時間段內高出其他時間段，如果在此時進行交易就可以獲得較高的收益。本文所研究的樣本數據選取了2010年5月4日至2014年7月5日內所有交易日的收盤價，這段時間是2008年金融危機后開始走向經濟復蘇時段，也是滬深300股指期貨推出到現今的大體時間。在研究時間范圍內，指數大體是呈下降的趨勢，但是走向平緩，沒有太大的波動。采集一組相同背景下具有相似特征的樣本，這便于開展研究，也使得研究結果更具可信度。

二、文獻綜述

美國學者Osborne（1962）最早研究周日效應的。后來Cross（1973）和French（1980）運用美國500家上市公司股票指數的標普500指數（S&P 500 Index）進行了日歷效應研究和實證檢驗。他們的研究結果表明在美國的股票市場中存在著最高平均收益率出現在星期五的周內效應。在國內，俞喬較早對上海和深證股市進行研究，研究發現，周末效應同樣存在于上海和深證股票市場。徐國棟等人研究結果表明，季節效應明顯的存在于上海股票市場，而在深圳股票市場并不明顯。郭彥峰等對滬深300指數進行了相關的研究，他們的研究結果顯示指數中存在周內日歷效應。

三、模型設定與實證檢驗

1、樣本選取

本文通過同花順軟件，收集了滬深300股指期貨從2010年5月4日到2014年7月5日每個交易日的成交量和收盤價作為研究樣本，有效樣本各為1010個。然后再對數據進行對數處理，得到每個交易日的對數收益率和成交量變化率，有效樣本數各為1009個。本文在計算的過程中為了減少檢驗誤差對所有的樣本數據進行了對數處理。由于對數收益率和成交量變化率都比較小，所以將數據擴大100倍，目的是方便計算和統計。

分別對收盤價和成交量進行對數處理，計算公式如下：

其中rt代表的是t日當天的對數收益率，pt代表的是t日當天的收盤價格，pt-1代表的是t日前一天的收盤價格，即t-1日的收盤價格。dcjlt代表的是t日當天的成交量變化率，cjlt代表的是t日當天的成交量，cjlt-1代表的是t日前一天的成交量，即t-1日的成交量。

2、數據處理

對每個交易日的對數收益率做簡單的描述性統計分析，得到表1如下：

從表1的描述統計可以看出：對數收益率平均值在星期三和星期五時都是正數，其中星期五的平均值最大，為0.163，而其余三日的平均值為負數，其中星期四的平均值最小，為-0.2572；從偏度來看，星期三和星期四這兩天都是往右偏，其他三日均往左偏；從峰度來看，星期五的峰度為4.0168，大于3，表示比正太分布要陡峭一些，其余四日峰度均比3要小，所以比正太分布平坦。再從JB統計量可以看出，每個交易日以及總體的對數收益率均不服從正態分布。

對每個交易日的成交量變化率進行簡單的描述性統計分析，得到表2如下：

從表2的描述統計可以看出：星期一和星期四這兩日的成交量變化率平均值為正數，其中星期一的最大，為3.1675。其余三日均為負數，其中星期三的最小，為-1.9791；從偏度來看，成交量變化率在一周中均往右偏。再從JB統計量可以看出，每個交易日以及總體的成交量變化率均不服從正態分布。

3、ARCH模型檢驗

借鑒陳龍的研究，本文構建如下ARCH模型。

為了驗證ARCH效應是否存在于一個模型的殘差中，通常可以采用拉格朗日乘數檢驗（ARCH LM檢驗）以及殘差平方相關圖檢驗這兩種方法。本文選取了在本文研究時間范圍內的各交易日收盤價作為樣本序列，并對該樣本序列進行相關的驗證。將樣本序列進行對數處理是為了減少誤差。

初步設定模型的基本形式為：

其中因變量Y所代表的是spt，表示在t日當天的對數收盤價；自變量X代表spt-1，表示在t-1日當天的對數收盤價。

（1）單位根檢驗

如果序列中存在單位根，那就說明這不是一個平穩的序列，假如對不平穩的序列進行回歸分析，會使得結果存在誤差，因此要對序列進行單位根檢驗。檢驗結果見表3。

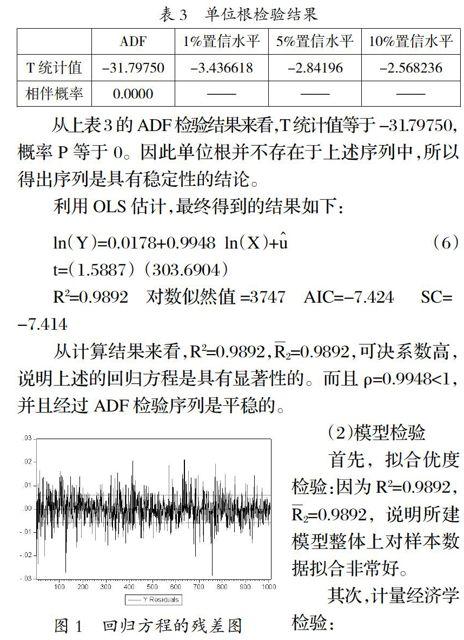
從上表3的ADF檢驗結果來看，T統計值等于-31.79750，概率P等于0。因此單位根并不存在于上述序列中，所以得出序列是具有穩定性的結論。

利用OLS估計，最終得到的結果如下：

從計算結果來看，R2=0.9892，R2=0.9892，可決系數高，說明上述的回歸方程是具有顯著性的。而且？籽=0.9948<1，并且經過ADF檢驗序列是平穩的。

（2）模型檢驗

首先，擬合優度檢驗：因為R2=0.9892，R2=0.9892，說明所建模型整體上對樣本數據擬合非常好。

其次，計量經濟學檢驗：

最后，異方差檢驗：通過對圖1的觀察，可以發現在殘差圖中產生了波動成群的現象，說明模型可能存在異方差。因此，繼續進行ARCH LM檢驗，最終得到滯后七階的檢驗結果見表4。

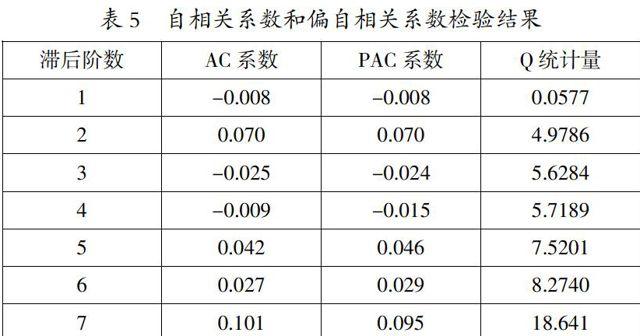
此時的概率P值等于0.0111，即在5%的顯著水平下拒絕回歸方程中不存在ARCH效應的原假設，說明了ARCH效應存在于回歸方程的殘差序列存中。此外，我們從AC系數和PAC系數也能夠驗證上訴結論（見表5）。

從表5可以看出，無論是AC圖還是PAC圖，在滯后二階和七階時都超出了區間范圍，其他階都在區間范圍內。因為在滯后二階和七階的AC系數和PAC系數均顯著不等于0，并且相對應的Q統計量較為顯著，因此可以得出：ARCH效應存在于模型的殘差序列中。

四、結論與政策建議

既然滬深300股指期貨存在著周內日歷效應，說明該市場并不是有效的市場。為了提高投資收益率，投資者在進入或者退出投資市場時，可以結合實際情況來利用已掌握到的日歷效應信息，通過日歷效應來改善自身的投資策略，從而更好的規避風險。比如，在星期五的平均收益率最高，就可以在其他平均收益率低的交易日進行買入操作，或者在星期五進行賣出操作。當然，我們并不能單單籠統的運用日歷效應來進行市場操作，因為市場是多變的，要預測市場的變動需要考慮到多種因素的綜合作用。

（注：本文系廣西哲學社會科學十二五規劃項目（項目編號：11EMZ014）和桂林旅游學院科研項目（項目編號：2011QN01）。）

【參考文獻】

[1] 徐國棟、田祥新、林丙紅：中國股市季節效應實證分析[J].廣西財政高等專科學校學報，2004（10）.

[2] 郭彥峰、魏宇：我國股指期貨標的指數的日歷效應研究[J].西南交通大學學報（社會科學版），2007（5）.

[3] 郭彥峰、黃登仕、魏字：上海期貨市場收益和波動的周日歷效應研究[J].管理科學，2008（4）.

（責任編輯：諶盼）