吉首大學軟件工程專業綜合改革試點之

康國棟 鐘鍵

當前，社會各行業對軟件人才的需求日益增長，雖然我國高校軟件專業畢業生很多，但大部分進入企業后的畢業生主動或被動定位為“碼農”，往往因跟不上產業的迅猛發展與技術的快速更新而倍感壓力，簡單的認為軟件行業是“青春飯”行業，進而選擇辭職轉業;與之相對應的是，許多軟件企業招聘不到合適的人才， 甚至不愿聘用畢業生。實際上，企業真正缺少的是能夠快速理解軟件架構及編碼核心思維并能根據新技術、新潮流創新求變的人員，這類專業人才必然要具有良好的思維能力與數學素養。 ?離散結構課程是軟件工程專業基礎課，一般由計算機學科專業的教師負責教學，其作用有別于高等數學、線性代數等公共數學課程。 然而軟件工程專業本科學生往往意識不到離散數學與軟件科學之間的關系，誤將其看作公共數學課，學習興趣不高、主動性較差，更談不上將課程內容與軟件科學領域實踐相結合[1]。 針對這種情況，部分軟件工程專業教師提出了相應的教學改革思路：大幅壓縮理論課教學，大力加強實踐教學，把一些經典的應用案例及解決模式傳授給學生，然后讓學生大量練習套用所學模式解決常見技術問題。 但一段時間的實踐證明，該理念易于使軟件工程專業本科教育傾向于技術培訓與強化訓練， 偏離了軟件工程專業本科教育人才培養目標。 因此，客觀認識離散結構課程的教學目標并實施該課程教學的綜合改革是實現人才培養目標的需要。

一 思路與舉措

結合筆者近年來的教學實際，借鑒國內多位名師的教學理論與實踐經驗，下面介紹筆者以思維與應用有機結合為核心理念（“思維——應用”）進行教學綜合改革的思路與具體舉措。

1 研究優化教學內容

目前，國內出版的高等院校離散數學類教材，一般包含四個部分：集合論、數理邏輯、代數系統和圖論，也有部分計算機專業的離散數學教材把二元關系從集合論中剝離開來，單獨作為一部分。國內教材的特點是數學性強，結構明確，側重概念、定理、推理與證明，但實例較少[2-4]。而國外經典離散數學教材，以Discrete Mathematics and Its Applications 一書為例[5-6]，結構為：邏輯、集合、函數基礎、算法整數矩陣基礎、數學推理、計數、高級計數技術、關系、圖、樹、布爾代數、計算模型。其特點是：一方面概念的引入、定理的詮釋高度數學抽象，學生短時間內難以入門;另一方面側重于實際問題的引入，實例多而精彩，但體系龐大不易把握。 因此， 國內外教材各有其優越性。 為此，教研組選擇了邵學才、葉秀明等編寫的《離散數學》作為理論課教材[7]。該教材知識點清晰，概念的引入，定理的描述推導相對淺顯易懂，便于學生掌握。并且把該教材集合論基礎理論部分、函數部分定為學生自學內容，刪節了代數系統的環和域的理論部分;實例部分則由教研組綜合比較國外系列教材，共同研究具體實踐案例。

2 精選教學案例

在有限的教學時間內，既要保證學生對離散數學知識點的理解掌握，又要培養學生使用離散數學思維解決軟件工程領域實際問題的意識，這就對教學案例的選取有較高要求。鑒于文獻[8]的研究，以下是筆者在教學過程中采用的部分精選案例。

（1）集合論、二元關系

此部分內容中集合論的知識較容易理解（自學），但涉及到“關系”知識點時，由于新的概念、定義較多，學生往往接受困難。針對該知識點，教學中的首要目標是讓學生把握關系的實質，選用的實例多用來說明關系在軟件工程領域中的應用。以常見關系數據庫SQL Server為例，使學生意識到關系的本質就是一些n 元組的集合，而且關系的運算本質可轉化為矩陣運算（注意：矩陣運算是先期線性代數課程的重要知識點），因此舉實例時， 可以先介紹矩陣運算在加密解密、信息壓縮等方面的應用，激發興趣，而后介紹相關矩陣運算的計算機編碼實現技術。 進一步為加強學生的實踐能力，本章的重要知識點，判斷關系傳遞性的Warshall 算法設置為課外實驗題。

（2）數理邏輯

數理邏輯研究的核心問題是邏輯命題及系統推理。離散數學課程介紹了數理邏輯的基本內容，但是其眾多數學符號、定義、定理往往使學生陷入枯燥繁復的數學知識學習中[9]。為激發學生學習興趣、培養學生的“思維——應用”意識，在此部分教學中，我們選擇了布爾檢索、專家系統原理等實例。 邏輯聯結詞是數理邏輯中的基本知識點，就其本身概念來說，屬于易于掌握的知識點，合適的實例能使學生認識到該課程在軟件工程領域中的實際應用。 布爾檢索技術目前廣泛用于網絡資源、Web 頁面搜索中，大多數學生都使用過baidu、 google等搜索引擎。在這種背景下，我們設計了布爾檢索實例：先引入布爾檢索概念中，聯結詞AND 用于匹配包含兩個檢索項的記錄，聯結詞OR 用于匹配兩個檢索項之一或者兩項均匹配的記錄，而聯結詞NOT 用于排除某個特定的檢索項。進而設置了如下問題供討論：

問題：用布爾邏輯搜索北京市或上海市非985大學主頁。

答案：（（Beijing OR Shanghai）AND UNIVERSITIES） NOT 985（需要注意，AND 運算級別高于OR ）。該實例教學將布爾檢索中的這些概念緊密地與數理邏輯中的合取、析取、否定聯結詞知識點聯系起來，加深了學生對邏輯聯結詞的認識，更重要的是，引導學生以數理邏輯思維重新認識信息精確化定位檢索的實踐。

（3）圖論

圖論是離散數學的重點， 并且是數據結構等課程的基礎，與計算機、軟件工程科學的聯系較明顯，易于調動學生聯系其與軟件工程的意識。但是，圖論內容抽象、難度大，對低年級學生來講，難以過渡到用相關算法在計算機上編程模擬實際問題。 我們選用的理論課教材實例也多為趣味性問題，如旅行售貨員問題、代價最低網絡通路等問題。盡管如此，我們設置了一些課外實驗課題供學生選做。

二 研究改進教學方式

軟件工程專業的課程體系與傳統的計算機專業相比，基礎理論課時更少，再加上課程具有邏輯性強、抽象且難度大的特點，對本課程的教學方式提出了更高的要求。下面重點介紹筆者采用現代技術改進教學方式的主要舉措。

1 信息化教學資源建設

首先，重視多媒體教學資源設計。離散數學課程的特點是概念、性質多，傳統的板書效率低、教學效果差，而多媒體課件的醒目、美觀、可塑性能揚長避短。 關于這部分的內容我們綜合采用各位名家的教育理念與經驗[10-12]。 除了做到常規的要求（標題簡潔明了、條理清晰等）外，在概念的引入、講解中，重視圖文并茂，適量演示學生易接受的應用實例及實踐技術。

其次學院與深度合作企業建設了“高校智能移動學習云平臺”以下簡稱“移動云平臺”。 教研組實時向云服務器加載精選的電子教學資源（包括多媒體教學課件、擴展的教學視頻資源，如：慕課MOC資源等），更新實踐案例庫，為學生提供豐富多彩的網上教學資源，彌補課堂教學時效有限性。 實踐證明，“移動云平臺”的搭建及運用方便了學生自主學習和師生間的交互， 有利于指導學生進行個性化學習和協同學習，培養學生的學習能力和創新能力。

2 注重研討式教學

離散數學中基本概念、性質、定理較多，而且連貫性不明顯，單純地講解，枯燥乏味，難以激發學習熱情。而通過設置少量的研討課題，開展課堂研討式教學，并列入考核指標體系，可增強學生的學習積極性。在研討式課堂教學中，以小組單位，所有學生都能直接參與到所設置問題的討論中，回答問題或提出質疑，相互交流意見，有助于調節課堂氣氛，加深學生對理論知識的理解和記憶。 考慮到課堂教學時間有限，還可充分利用網絡平臺讓師生參與討論，增進師生、同學之間的交流。

三 配套考核模式

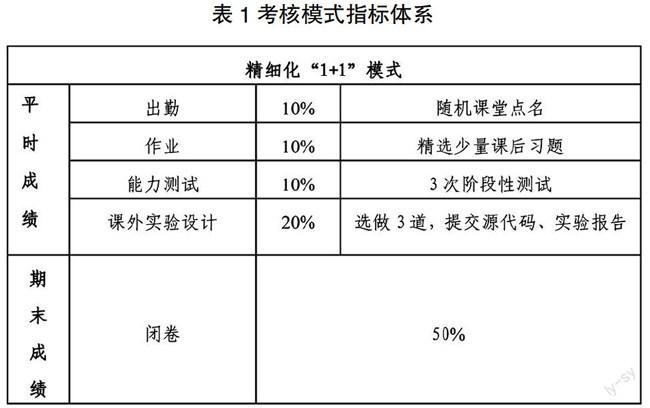
傳統的考核模式一般是粗放式“1+1”模式。隨著多種教學方法的運用，我們嘗試了配套的精細化“1+1”考核模式，細化了平時成績，強化了對思維能力與實踐能力的考核，詳見表1。

表1考核模式指標體系

其中，能力測試主要對學生進行隨堂考試，對有一定綜合性的理論知識或思考題進行解答;課外實驗設計成績的評價指標主要包括原理分析正確，程序邏輯清晰，代碼符合規范，實驗報告完整等。下面重點闡述我們在課外實驗設計教學環節上所作的一些改革。

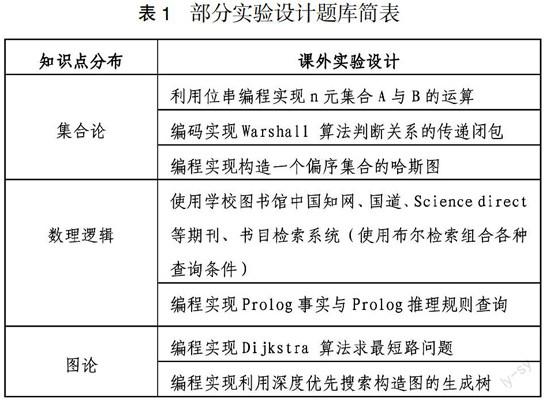
目前離散數學不提供上機實驗課時，如果僅僅讓實例停留于上課時的講解演示，無法進一步調動學生的自主性和動手能力[13-14]。因此，我們編寫了課外實驗設計指導講義（根據知識點分布，我們目前共設置了12個課外實驗題目），并在“移動云平臺”加載了對應的電子版，供學生自由選做其中3個（注意：每個知識點僅選一題）， 并在期末考核中占20%。以下僅列出部分實驗設計題庫簡表：

表1 ? 部分實驗設計題庫簡表

其中，圖論部分實驗設計對于計算機專業低年級本科生來說偏難。但是考慮到圖論是后續課程數據結構的基礎，數據結構課程將涉及到這些算法與編程實現，所以將其選編入課外實驗中，供學有余力的學生課外選作。上述課外實驗設計題目在教學過程中不斷增加，以期形成與時俱進的實踐題庫。

2011級5個教學班的大部分同學至少選作兩道題，均提交了源代碼、實驗報告的電子文檔。小部分同學提交了較多課外實驗報告，文檔、代碼水平較高，這部分同學的綜合成績普遍處于優秀級。另外，對于學生做好畢業設計也有潛在效果，教研組老師所指導的30名學生的畢業設計完成效率高，質量較好。體現了課外實驗對于提升學生綜合能力尤其是實踐能力的作用。

總之，借鑒國內名家的教育理論與教學經驗，本文從教學內容、教學方式、配套的考核模式等方面對吉首大學軟件工程專業綜合改革之離散結構的教學綜合改革舉措進行了探討。實踐證明，教學改革舉措的穩步實施增強了學生的學習興趣，促進了課程的教學效果，對提升學生的學習能力、實踐能力起到了良好的促進作用，尤其是加強了學生從思維到實際應用的意識，為學生今后的發展打下了堅實的基礎。 是適應軟件產業對人才需求趨勢，培養“思維——實踐”高層次軟件工程人才的具體實踐，是教育部湖南省吉首大學軟件工程專業“十二五”綜合改革試點的有機組成。

參考文獻

[1][11]韓春燕，朱志良，姜慧研，劉益先. 軟件工程專業離散數學的教學思考[J].計算機教育，2011（11）：68-70.

[2]左孝凌，李為鑑，劉永才.離散數學[M].上海：上海科學技術文獻出版社，1982.

[3]左孝凌，李為鑑，劉永才.離散數學[M].上海科技技術文獻出版社，2006.

[4][7]邵學才，葉秀明.離散數學[M].北京：機械工業出版社，2011.

[5] Kenneth H. Rosen. 離散數學及其應用（英文版5 版）

[M].北京：機械工業出版社，2007.

[6]Kenneth H. Rosen. Discrete Mathematics and Its Applications （4th Edition） [M].McGraw-Hillcompanies， Inc， USA， 2002.

[8] 師雪霖，尤 楓，顏可慶.離散數學教學聯系計算機實踐的探索[J].計算機教育，2008（20）：113-115.

[9]何鋒.離散數學教學中的命題符號化難點討論[J].計算機教育，2007（9）：38-40.

[10] 趙青杉，孟國艷.離散數學多媒體課件的開發與應用[J]. 計算機科學，2004，33（11）：304-305.

[13] 藺永政，王新紅，李金屏.“離散數學”中實踐教學的探討[J].計算機教育，2006（10）：103-104.

[14] 翁梅，劉倩，馮志慧，閭素紅.“離散數學”課程教學實踐與探索[J].計算機教育，2004（12）：62-63.