基于面光滑有限元的復雜三維結構拓撲優(yōu)化

何智成　陳少偉　李光耀　張桂勇

1.湖南大學汽車車身先進設計制造國家重點實驗室，長沙，4100822.大連理工大學工業(yè)裝備結構分析國家重點實驗室，大連，116023

基于面光滑有限元的復雜三維結構拓撲優(yōu)化

何智成1陳少偉1李光耀1張桂勇2

1.湖南大學汽車車身先進設計制造國家重點實驗室，長沙，4100822.大連理工大學工業(yè)裝備結構分析國家重點實驗室，大連，116023

為了增強拓撲優(yōu)化計算對任意復雜模型的適應性，改進基于線性四面體有限元的拓撲優(yōu)化結果，引入了一種新型高精度的基于面光滑有限元模型(FS-FEM)來進行拓撲優(yōu)化，通過每次迭代時提供很好的梯度解及位移解，從而達到改善拓撲優(yōu)化結果的目的。在基于面光滑有限元模型的拓撲優(yōu)化中，以柔度最小作為目標函數(shù)，建立了基于固體各向同性材料懲罰插值(SIMP)的拓撲優(yōu)化數(shù)學模型，該數(shù)學模型通過最優(yōu)準則進行求解。多個不同載荷的拓撲優(yōu)化數(shù)值算例說明，采用基于面光滑有限元進行拓撲優(yōu)化，結果都能夠單調(diào)收斂，且采用該方法建立的拓撲優(yōu)化模型能抑制棋盤格現(xiàn)象。與商業(yè)軟件OptiStruct的計算比較表明，該方法相比有限元方法能得到更合理的拓撲結構。

拓撲優(yōu)化；光滑伽遼金；面光滑有限元；四面體單元

0　引言

在產(chǎn)品的開發(fā)中，保證產(chǎn)品性能的同時減小質量已經(jīng)成為當前航空航天、機械、汽車等領域中一個重要的研究方向，因而優(yōu)化技術已經(jīng)廣泛應用到各個領域。隨著工程結構或產(chǎn)品越來越復雜，現(xiàn)有的優(yōu)化技術一般都在基于離散單元的基礎上進行，如拓撲優(yōu)化主要基于現(xiàn)有的有限元技術，通過在給定的設計空間施加載荷及邊界條件來尋找材料的最佳分布，使得最終設計的零部件或產(chǎn)品具有很好的性能以及較小的質量。在過去的幾十年中，拓撲優(yōu)化取得了非常大的發(fā)展。目前常用的拓撲優(yōu)化方法有基于均勻化的方法[1]、基于密度的方法[2-3]、水平集法[4]、獨立連續(xù)體映射模型方法[5]等。其中，變密度法具有較高的計算效率，在工程中應用最為廣泛。其他結構拓撲優(yōu)化方法還包括基于進化策略的進化結構法[6]等，Rozvany[7]對其進行了系統(tǒng)的綜述。近年來，高階單元法[8]以及無網(wǎng)格法[9-10]也被用于連續(xù)體結構的拓撲優(yōu)化研究，研究結果表明，新型高精度數(shù)值方法能夠消除棋盤格現(xiàn)象，使邊界變得較為光滑，能很好地改進拓撲優(yōu)化的結果。

在基于有限元的拓撲優(yōu)化中，四面體能夠對任意復雜的工程結構進行很好的網(wǎng)格剖分，適用于任意復雜工程結構的計算，然而由于線性四面體單元的剛度過大，在計算位移場和梯度場時存在較大的數(shù)值誤差，故在拓撲優(yōu)化中，不能得到很好的拓撲優(yōu)化結構。另外，由于拓撲優(yōu)化得到的零部件的材料分布或形狀不規(guī)則、邊界不光滑[11]以及存在網(wǎng)格依賴性(mesh-dependency)和棋盤格式(checkerboards)等數(shù)值計算缺陷[11]，難以滿足工程制造的要求，故拓撲優(yōu)化仍然存在著很大的挑戰(zhàn)。現(xiàn)有基于離散單元的拓撲優(yōu)化技術基本都是基于三維六面體單元的研究，然而六面體對復雜零件的幾何形狀表征能力差，不能對復雜的三維工程結構進行離散，因而，基于六面體單元的拓撲優(yōu)化不能對復雜三維模型進行優(yōu)化。

為了增強拓撲優(yōu)化計算對任意復雜模型的適應性，改進基于線性四面體有限元的拓撲優(yōu)化結果，本文通過引入一種新型高精度的基于面的光滑有限元模型(face-based smoothed finite element method, FS-FEM)[12-13]來進行拓撲優(yōu)化，通過每次迭代時提供很好的梯度解及位移解來達到改善拓撲優(yōu)化結果的目的。本方法通過對單元內(nèi)的應變分片進行光滑操作，并形成剛度矩陣，從而使得整個模型的剛度趨于柔軟，恰好部分地抵消傳統(tǒng)線性單元過于剛硬帶來的誤差，從而提高了單元計算的精度，因而該方法對于拓撲優(yōu)化具有很好的應用前景。本文在基于面的光滑有限元拓撲結構優(yōu)化中，以柔度最小為目標函數(shù)，以基于面的光滑域作為設計的變量，并采用固體各向同性材料懲罰插值(solid isotropic material with penalization,SIMP)方法來建立拓撲優(yōu)化的數(shù)學模型，通過優(yōu)化準則來進行求解。最后通過三個不同載荷工況的數(shù)值算例來驗證本方法的有效性。

1　三維彈性力學方程

對于連續(xù)材料的模型,其彈性介質的小變形控制方程可以使用下式進行表示:

LTσ+b=0

(1)

其中，σ為應力張量,b為體力向量, L為矩陣的微分算子。對于各向同向材料，應力和應變具有如下關系:

σ=D ε

(2)

其中， D為材料矩陣;ε 為應變張量，且與位移u具有如下幾何關系：

ε=L u

(3)

一般的固體力學問題具有兩類邊界條件，一類是Dirichlet邊界條件，另一類是Neumann邊界條件。

(1)自然邊界條件可以表示為

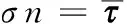
(4)

(2)位移邊界條件可以表示為

(5)

2　基于面的光滑應變技術

在FS-FEM的構造中, 問題域中的應變不再采用有限元中的協(xié)調(diào)應變形式ε=L u, 而是采用光滑應變的形式。該光滑應變是通過在光滑域內(nèi)對不連續(xù)的應變進行梯度光滑操作而形成的。通過對所有光滑域的組裝，即

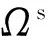
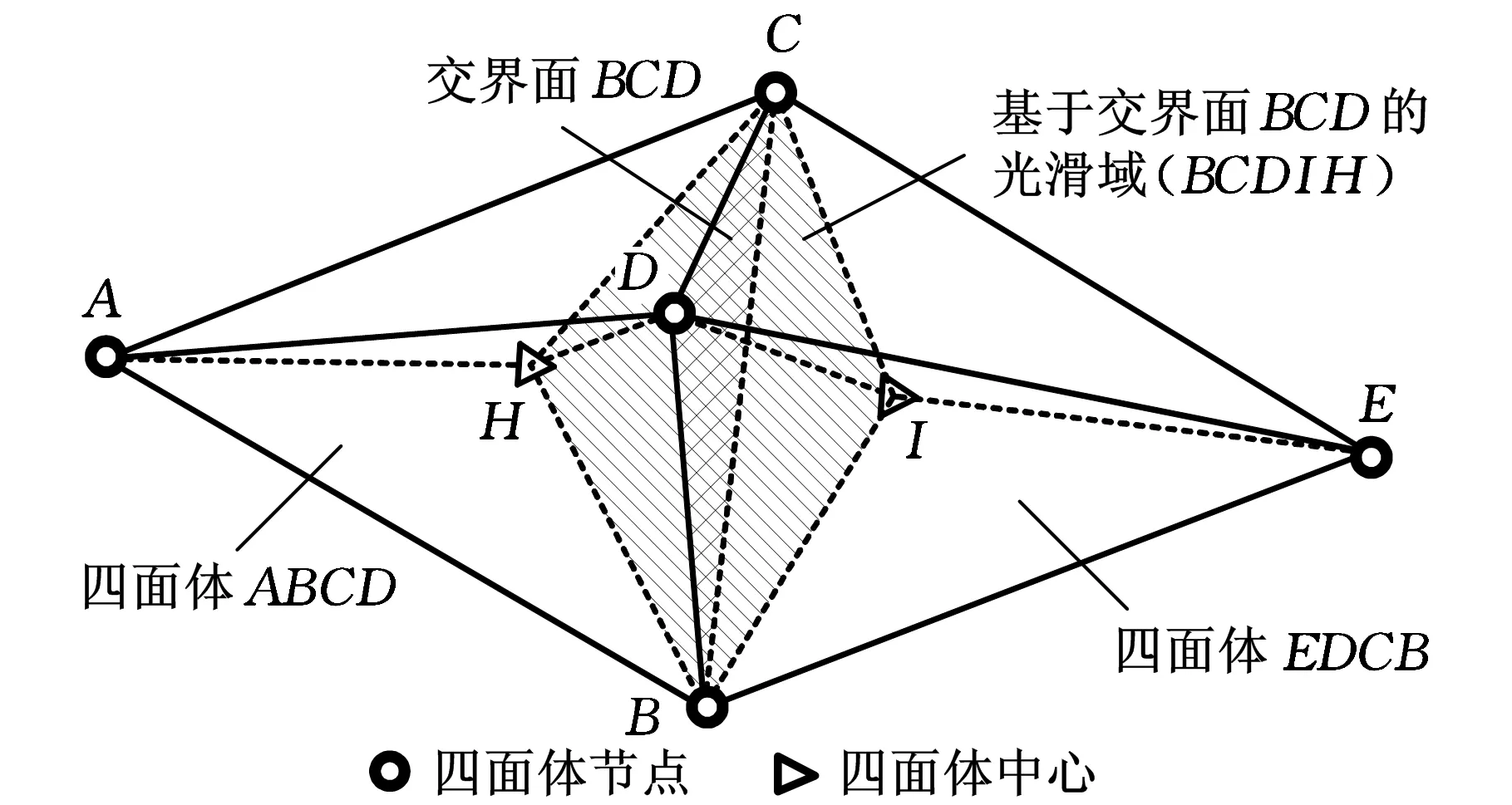
圖1　基于面的三維光滑域

(6)

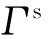
(7)

(8)

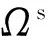
(9)

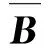
(10)

(11)

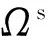
(12)

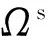
3　基于面的光滑有限元模型的建立

在彈性力學中，假定整個的問題域為Ω，其邊界為Γ(Γ=Γu+Γt)，其廣義光滑Galerkin的弱形式可以寫成如下形式[13]：

∫ΓtδuTtΓdΓ=0

(13)

其中，δ為變分因子。將式(6)、式(8)代入式(13),最后的離散線性方程組可以寫成如下形式:

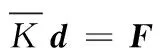
(14)

(15)

(16)

(17)

(18)

式(18)是基于線性四面體的常應變單元來進行推導的(應變矩陣為常數(shù))。由于應變矩陣是基于有限元的形函數(shù)進行的推導，故可以看出，三維FS-FEM的剛度矩陣為對稱稀疏矩陣，可以使用通用的求解器進行線性方程組的高效率求解。

4　基于面光滑有限元的拓撲優(yōu)化模型

4.1基于SIMP材料插值的拓撲優(yōu)化模型

近年來，基于剛度-密度插值的模型由于實現(xiàn)簡單，因而在拓撲優(yōu)化中應用得最為廣泛。其中，基于正交各向同性材料密度冪指數(shù)形式的變密度法材料密度插值理論方法是最常見的一類剛度-密度插值模型，本文也基于該類模型來實現(xiàn)拓撲優(yōu)化。基于SIMP材料插值模型假設材料的彈性模量Ep可以表示成如下形式[11]：

E(x)=ρ(x)pE0

(19)

其中，ρ(x)為設計變量，p為冪指數(shù)懲罰函數(shù)，通過引入懲罰因子，對中間密度進行懲罰，盡量使優(yōu)化過程中的密度趨近“0”(表示無材料)或“1” (表示有材料)，E0為給定各向同性材料的彈性模量，E為插值的材料彈性模量。

在基于面光滑的有限元中，由于以四面體的面光滑域作為組裝整體剛度矩陣的基本單位，故可以選取基于面光滑域的密度作為設計變量。因此，在基于面光滑有限元模型的拓撲優(yōu)化中，以柔度最小(即結構應變能最小，剛度最大)作為目標函數(shù)，以結構的體積比為約束條件，則基于SIMP模型的拓撲優(yōu)化數(shù)學模型可以表示為

(20)

其中，目標函數(shù)c為結構的總柔度，由各個光滑域相加得到。V0、V分別為優(yōu)化前和優(yōu)化后設計域內(nèi)的材料體積；f為體積分數(shù)；ρ為設計變量，表示面光滑域的密度，取值范圍為0～1，但是為了保證數(shù)值分析的穩(wěn)定性，避免出現(xiàn)奇異矩陣，通常選取一個非常小的值作為設計變量的下限ρmin，本文取0.01。

建立拓撲優(yōu)化的數(shù)學模型后，可以采用多種優(yōu)化方法對其求解，如優(yōu)化準則法 (optimalitycriteria,OC)[11]、序列線性規(guī)劃法(sequentiallinearprogramming,SLP)[14]以及移動近似算法(MMA)[15]等。OC算法是一種間接優(yōu)化算法，它并不是直接對目標函數(shù)進行優(yōu)化求解，而是利用Kuhn-Tucker條件作為最優(yōu)解的滿足準則，其算法收斂速度快，迭代次數(shù)少，這對于設計變量多、連續(xù)體拓撲結構的復雜優(yōu)化求解是一種高效率高精度的方法[3]。基于SIMP材料插值模型的優(yōu)化準則法的迭代格式如下：

(21)

其中，η(0<η<1)為阻尼因子，m為移動極限，用來控制迭代的步長。通過在迭代過程中引入這兩個參數(shù)來保證設計變量迭代過程穩(wěn)定，參數(shù)B通過OC準則得到，其表達式為

(22)

其中，λ為拉格朗日乘子，通過二分法得到。其迭代中止條件為

‖(ρnew-ρ)/ρnew‖≤ξ

(23)

4.2靈敏度分析

由式(22)可知，采用優(yōu)化準則求解優(yōu)化問題時，需要用到目標函數(shù)關于設計變量的導數(shù)，即目標函數(shù)對設計變量的靈敏度。通過對柔度求導，得到

(24)

(25)

將式(25)代入式(24)得

(26)

這樣，目標函數(shù)的靈敏度就轉化為求解剛度矩陣關于設計變量的靈敏度。

4.3敏度過濾及密度插值

在基于有限元的拓撲優(yōu)化中，普遍存在網(wǎng)格依賴和棋盤格等數(shù)值不穩(wěn)定的現(xiàn)象，尤其在低階的單元中[11]。為了保證拓撲優(yōu)化得到較好的數(shù)值解，許多學者對其進行了研究。許多研究表明，基于敏度過濾的方法能夠很好地解決網(wǎng)格依賴和棋盤格問題[11]。敏度過濾的主要思想是在求解某個指定單元靈敏度時，取其周圍相鄰單元的靈敏度值加權平均。由于敏度過濾的方法沒有增加額外的約束，故在計算量上不會造成大的負擔，簡單易用。敏度過濾是通過在迭代中改變單元的靈敏度來實現(xiàn)過濾的。而在基于面光滑有限元的拓撲優(yōu)化中，在求解某個光滑域的靈敏度時，取相鄰光滑域的靈敏度進行平均，公式為

(27)

其中，M是定義敏度過濾的半徑內(nèi)的所有光滑域的個數(shù)；Hf是權系數(shù)，也是卷積運算符表達式，即

(28)

其中，rmin是敏度過濾半徑，|xi-xf|表示光滑域i的中心點與光滑域f中心點之間的距離(若其距離超出了過濾半徑，則權重為0)。在敏度過濾技術中，靈敏度的權重是根據(jù)兩個單元之間的距離來控制的，過濾半徑大小的選擇在一定程度上也會影響過濾效果。在過濾技術中，對優(yōu)化結果的控制主要是通過調(diào)節(jié)過濾半徑rmin來實現(xiàn)的，通過選擇合適的過濾半徑rmin即可得到穩(wěn)定收斂的優(yōu)化結果。

在FS-FEM的拓撲優(yōu)化中，由于計算得到的是面光滑域的密度，筆者又引入一層密度過濾技術，將面光滑域的密度轉化為單元的節(jié)點密度，則節(jié)點密度與面光滑域密度的關系為

(29)

其中，ρi為節(jié)點i的密度,n為包含節(jié)點i的面光滑域的個數(shù)，ρk為以面k為中心的光滑域的密度。

5　數(shù)值算例

本節(jié)采用3個三維拓撲優(yōu)化算例來對本文提出的方法和模型進行驗證。算例一為單點載荷下的三維結構拓撲優(yōu)化，是拓撲優(yōu)化的經(jīng)典算例。由于在實際的優(yōu)化中，一般結構都具有多個載荷，故算例二針對結構的多載荷工況進行了拓撲優(yōu)化；另外由于在實際的應用中，結構和載荷一般都比較復雜，故算例三也針對復雜結構復雜載荷下的汽車懸架下擺臂進行了研究。在本文前兩個算例的模型中，材料的彈性模量均為1Pa,泊松比為0.3，模型采用通用的線性四面體網(wǎng)格進行離散，算例的計算在MATLAB軟件中編程實現(xiàn)。

5.1基于單點載荷三維懸臂梁模型

圖2所示為三維懸臂梁，其尺寸為8m×4m×8m，其左端面約束，其右端面下邊界中間受到單個集中載荷的作用，其力的大小為1N。該設計域被離散成1920個節(jié)點、8071個四面體單元，取體積分數(shù)的約束為0.4。采用FS-FEM對其進行拓撲優(yōu)化研究。首先研究懲罰因子p對其收斂性的影響。圖3為懲罰因子分別為2、3、4的收斂曲線圖，可以看到當p為3和4時收斂較快，迭代43次后收斂，p值取2時，迭代次數(shù)要比懲罰因子為3和4時的迭代次數(shù)大很多。這說明懲罰因子取p≥3比較合適。

圖2　三維懸臂梁模型示意圖

圖3　基于單點載荷拓撲優(yōu)化的目標函數(shù)收斂示意圖

圖4a為收斂后的拓撲結構示意圖，為了便于比較，采用商業(yè)計算軟件OptiStruct進行計算，其結果見圖4b。兩者結構類似，但是根據(jù)文獻[1]的二維類似問題比較，發(fā)現(xiàn)基于面光滑有限元的結果更接近參考解的拓撲結構。

(a)FS-FEM的優(yōu)化計算結果(b)OptiStruct的優(yōu)化計算結果圖4　拓撲優(yōu)化計算結果比較

5.2基于多載荷的三維拓撲優(yōu)化設計

在實際應用中，大多數(shù)工程結構都工作在多載荷工況下，因此，對多載荷工況下連續(xù)結構拓撲優(yōu)化問題進行研究具有現(xiàn)實的工程應用價值。圖5所示為三維立方體模型，其尺寸為100m×100m×100m，其下端4個頂點約束，在頂面內(nèi)受到垂直4個集中載荷的作用，其力的大小為1N。采用FS-FEM對其多載荷的拓撲結果進行優(yōu)化。首先將該設計域離散成7284個節(jié)點、35 648個四面體單元，取體積分數(shù)的約束為0.4。圖6為采用FS-FEM計算得到的目標函數(shù)的收斂曲線圖，可以看出該模型是單調(diào)收斂的。

圖5　多載荷模型示意圖

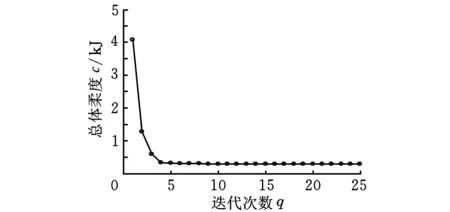
圖6　多載荷拓撲優(yōu)化的目標函數(shù)收斂示意圖

圖7為收斂后的的拓撲結構示意圖，為了便于比較，圖8、圖9所示分別為采用商業(yè)計算軟件OptiStruct計算的結果以及文獻[16]提供的結果。可以看出，采用FS-FEM計算的結果比OptiStruct計算的結果更加接近文獻[16]的結果。

圖7　FS-FEM的優(yōu)化計算結果

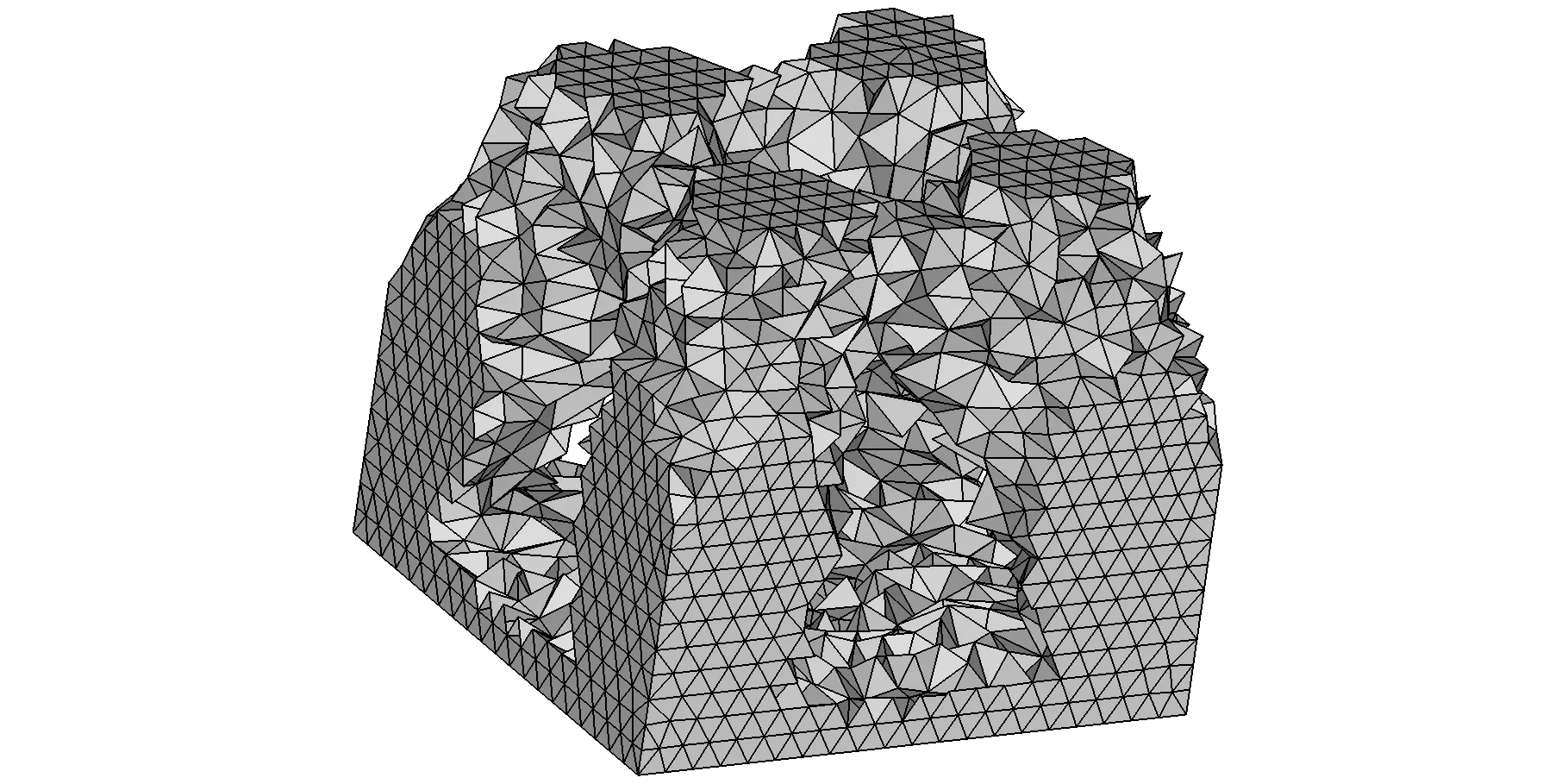
圖8　OptiStruct的優(yōu)化計算結果

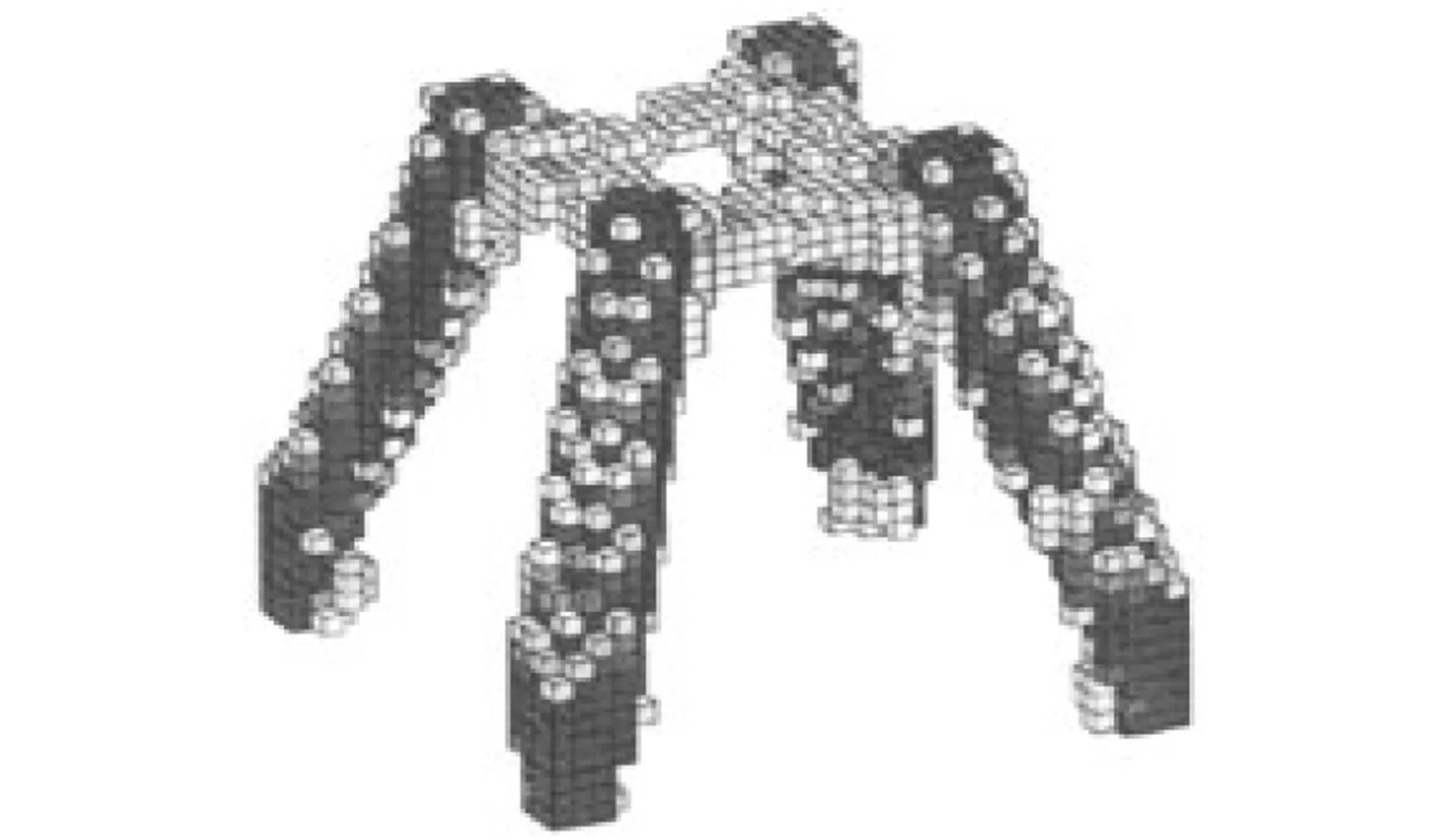
圖9　OOlhoff等[16]計算的結果

5.3汽車懸架下擺臂的拓撲優(yōu)化

近年來，輕量化是汽車的結構設計非常關注的研究方向。汽車零部件的輕量化是指在不影響零部件剛度等性能的基礎上，通過設計質量小的產(chǎn)品達到降低汽車制造成本的目的。由于拓撲優(yōu)化能夠在給定的邊界條件下得到最優(yōu)的材料分布，因而在汽車中的應用越來越廣泛。本節(jié)針對具有復雜載荷的汽車懸架下擺臂進行研究，來驗證FS-FEM在復雜汽車零部件設計中的應用。圖10為汽車下擺臂的設計空間示意圖。由于下擺臂的左端的兩個鉸鏈與副車架相連，邊界條件為約束其中一個鉸鏈的xyz自由度，以及約束另外一個鉸鏈的yz自由度，另外，由于下擺臂的右端與車輪相連，需要承受來自x向、y向、z向的力，因此在鉸鏈中心的x向、y向、z向施加1kN的作用力。該下擺臂的材料為壓鑄鋁，其材料參數(shù)如下：彈性模量為79GPa，泊松比為0.3。

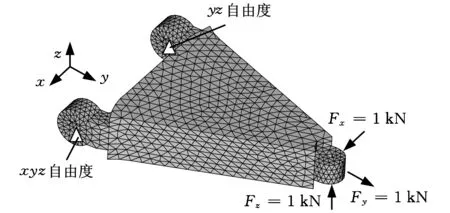
圖10　汽車懸架下擺臂設計空間及邊界條件示意圖

首先采用FS-FEM方法來對其進行拓撲優(yōu)化研究，該模型離散成2372個節(jié)點、9819個四面體單元，其體積分數(shù)約束為0.4。圖11為采用FS-FEM計算得到的目標函數(shù)的收斂曲線，可以看出該模型單調(diào)收斂。圖12為收斂后的拓撲結構示意圖，為了便于比較，采用商業(yè)計算軟件OptiStruct分別對離散的四面體模型和六面體模型進行計算，其結果分別在圖13、圖14中給出。可以看出，采用四面體有限元計算的拓撲結構雖然為穩(wěn)定的三角形結構，但是邊界不光滑，優(yōu)化后的拓撲結構不對稱；而采用FS-FEM計算的拓撲結果與OptiStruct采用六面體的計算結果非常類似，為穩(wěn)定的三角形結構，并且FS-FEM計算的拓撲邊界比六面體網(wǎng)格的計算結果具有較好的連續(xù)性，這說明FS-FEM能很好地對復雜零部件進行拓撲優(yōu)化。

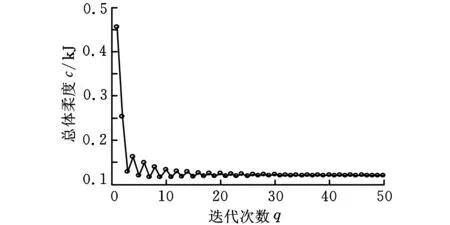
圖11　汽車懸架下擺臂拓撲優(yōu)化的目標函數(shù)收斂示意圖

圖12　FS-FEM的優(yōu)化計算結果

圖13　基于四面體離散的OptiStruct優(yōu)化計算結果

圖14　基于六面體離散的OptiStruct優(yōu)化計算結果

6　結論

(1)本文方法采用對問題域適應性很好的四面體網(wǎng)格來進行離散，對任何復雜的幾何模型具有很好的適應性，適用于任意復雜三維結構的拓撲優(yōu)化。

(2)基于面光滑的有限元能夠提供很好的梯度解，因而進行拓撲優(yōu)化計算的結構都能夠單調(diào)收斂。

(3)采用本方法建立的拓撲優(yōu)化模型能抑制了棋盤格現(xiàn)象，通過與商業(yè)軟件OptiStruct的計算結果進行比較，發(fā)現(xiàn)相比有限元法，本文方法能得到更合理的拓撲結構，邊界具有更好的連續(xù)性，具有很好的應用前景。

[1]BendsoeMP,KikuchiN.GeneratingOptimalTopologiesinStructuralDesignUsingaHomogenizationMethod[J].Comput.MethodsAppl.Mech.Eng.，1988，71(2):197-224.

[2]BendsoeMP,SigmundO.MaterialInterpolationSchemesinTopologyOptimization[J].Arch.Appl.Mech., 1999,69(9/10):635-654.

[3]羅震.基于變密度法的連續(xù)體結構拓撲優(yōu)化設計技術研究[D].武漢:華中科技大學, 2005.

[4]ChallisJV.ADiscreteLevel-setTopologyOptimizationCodeWritteninMATLAB[J].Struct.Multidisc.Optim.,2010,41(3):453-464.

[5]隋允康, 楊德慶.多工況應力和位移約束下連續(xù)體結構拓撲優(yōu)化[J].力學學報, 2000, 32(2): 171-179.

SuiYunkang,YangDeqing,WangBei.TopologicalOptimizationofContinuumStructurewithStressandDisplacementConstraintsunderMultipleLoadingCases[J].ActaMech.Sin.,2000,32(2): 171-179.

[6]XieYM,StevenGP.ASimpleEvolutionaryProcedureforStructuralOptimization[J].Comput.&Struct., 1993,49(5):885-896.

[7]RozvanyGIN.ACriticalReviewofEstablishedMethodsofStructuralTopologyOptimization[J].Struct.Multidisc.Optim., 2010,37(3):217-237.

[8]BruggiM.OntheSolutionoftheCheckerboardProbleminMixed-FEMTopologyOptimization[J].Comput.&Struct., 2008,86(19/20):1819-1829.

[9]ZhengJ,LongSY,XiongYB,etal.ATopologyOptimizationDesignfortheContinuumStructureBasedontheMeshlessNumericalTechnique[J].CMES:Comput.Model.Eng.&Sci., 2008,34(2):137-154.

[10]ZhouJX,ZouW.MeshlessApproximationCombinedwithImplicitTopologyDescriptionforOptimizationofContinua[J].Struct.Multidisc.Optim., 2008,36(4):347-353.

[11]Bends?eMP,SigmundO.TopologyOptimizationTheory,MethodsandApplications[M].NewYork:Springer, 2003.

[12]Nguyen-ThoiT,LiuGR,LamKY,etal.AFace-basedSmoothedFiniteElementMethod(FS-FEM)for3DLinearandGeometricallyNonlinearSolidMechanicsProblemsUsing4-nodeTetrahedralElements[J].Int.J.Numer.Mech.Engrg.,2009,78(3):324-353.

[13]LiuGR.AGeneralizedGradientSmoothingTechniqueandtheSmoothedBilinearFormforGalerkinFormulationofaWideClassofComputationalMethods[J].Int.J.ComputationalMethods, 2008,5(2): 199-236.

[14]FujiiD,KikuchiN.ImprovementofNumericalInstabilitiesinTopologyOptimizationUsingSLPMethod[J].Struct.Multidisc.Optim., 2000,19(2):113-121.

[15]SvanbergK.TheMethodofMovingAsymptotes-aNewMethodforStructuralOptimization[J].Int.J.Numer.Meth.Engrg., 1987,24(2):359-373.

[16]OlhoffN,RonholtE,ScheelJ.TopologyOptimizationofThreeDimensionalStructuresUsingOptimumMicrostructures[J].Struct.Optim., 1998,16(1):1-18.

(編輯陳勇)

Topology Optimization Using FS-FEM for Complex Three-dimensional Models

He Zhicheng1Chen Shaowei1Li Guangyao1Zhang Guiyong2

1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082 2.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian,Liaoning,116023

The FS-FEM was proposed recently based on tetrahedral mesh, and showed great property in solid mechanics, such as providing very good gradient solutions. The topology optimization design of the continuum structures under static load was formulated in the scheme of FS-FEM. As the face-based smoothing domains were the sub-units of assembling stiffness matrix in the discretized system of smoothed Galerkin weak form, thus the relative density of face-based smoothing domains were served as design variables. In this formulation, the minimization compliance was considered as an objective function, and the mathematic of the topology optimization model was developed using the solid isotropic material with penalization (SIMP) interpolation scheme. The topology optimization problem was then solved by the optimality criteria method. Finally, the feasibility and efficiency of the proposed method were illustrated with several 3D examples that were widely used in the topology optimization design.

topology optimization; smoothed Galerkin weak form; face-based smoothed finite element method (FS-FEM);tetrahedral mesh

2014-03-05

國家自然科學基金資助項目(11202074)；湖南大學汽車車身先進設計制造國家重點實驗室自主研究課題(51375001)；工業(yè)裝備結構分析國家重點實驗室開放基金資助項目(GZ1403)

TH122DOI：10.3969/j.issn.1004-132X.2015.07.003

何智成，男，1983年生。湖南大學汽車車身先進設計制造國家重點實驗室助理研究員。主要研究方向為汽車振動噪聲、汽車輕量化。陳少偉，男，1981年生。湖南大學汽車車身先進設計制造國家重點實驗室博士研究生。李光耀，男，1963年生。湖南大學汽車車身先進設計制造國家重點實驗室主任、教授、博士研究生導師。張桂勇，男，1979年生。大連理工大學船舶學院教授、博士研究生導師。